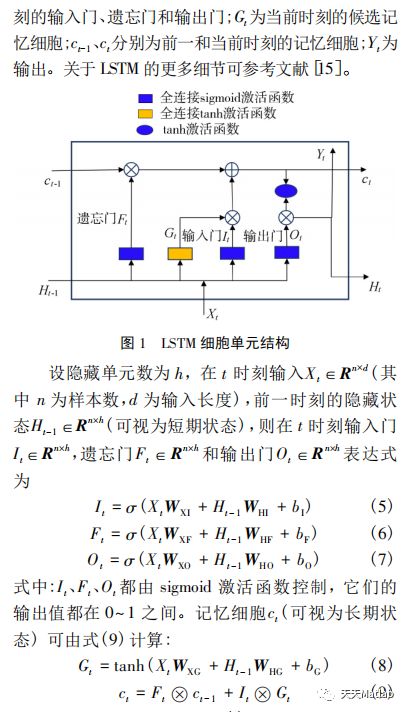
【LSTM时序预测】基于EMD结合长短时记忆网络LSTM实现风速数据预测Matlab源码

​✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab仿真内容点击

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

⛄ 部分代码

%EMD  computes Empirical Mode Decomposition

%这个是通过设定阈值来确定分解出的imf个数

%

%   Syntax

%

%

% IMF = EMD(X)

% IMF = EMD(X,...,'Option_name',Option_value,...)

% IMF = EMD(X,OPTS)

% [IMF,ORT,NB_ITERATIONS] = EMD(...)

%

%

%   Description

%

%

% IMF = EMD(X) where X is a real vector computes the Empirical Mode

% Decomposition [1] of X, resulting in a matrix IMF containing 1 IMF per row, the

% last one being the residue. The default stopping criterion is the one proposed

% in [2]:

%

%   at each point, mean_amplitude < THRESHOLD2*envelope_amplitude

%   &

%   mean of boolean array {(mean_amplitude)/(envelope_amplitude) > THRESHOLD} < TOLERANCE

%   &

%   |#zeros-#extrema|<=1

%

% where mean_amplitude = abs(envelope_max+envelope_min)/2

% and envelope_amplitude = abs(envelope_max-envelope_min)/2

% 

% IMF = EMD(X) where X is a complex vector computes Bivariate Empirical Mode

% Decomposition [3] of X, resulting in a matrix IMF containing 1 IMF per row, the

% last one being the residue. The default stopping criterion is similar to the

% one proposed in [2]:

%

%   at each point, mean_amplitude < THRESHOLD2*envelope_amplitude

%   &

%   mean of boolean array {(mean_amplitude)/(envelope_amplitude) > THRESHOLD} < TOLERANCE

%

% where mean_amplitude and envelope_amplitude have definitions similar to the

% real case

%

% IMF = EMD(X,...,'Option_name',Option_value,...) sets options Option_name to

% the specified Option_value (see Options)

%

% IMF = EMD(X,OPTS) is equivalent to the above syntax provided OPTS is a struct 

% object with field names corresponding to option names and field values being the 

% associated values 

%

% [IMF,ORT,NB_ITERATIONS] = EMD(...) returns an index of orthogonality

%                       ________

%         _  |IMF(i,:).*IMF(j,:)|

%   ORT = \ _____________________

%         /

%         ?       || X ||?%        i~=j

%

% and the number of iterations to extract each mode in NB_ITERATIONS

%

%

%   Options

%

%

%  stopping criterion options:

%

% STOP: vector of stopping parameters [THRESHOLD,THRESHOLD2,TOLERANCE]

% if the input vector's length is less than 3, only the first parameters are

% set, the remaining ones taking default values.

% default: [0.05,0.5,0.05]

%

% FIX (int): disable the default stopping criterion and do exactly  

% number of sifting iterations for each mode

%

% FIX_H (int): disable the default stopping criterion and do sifting 

% iterations with |#zeros-#extrema|<=1 to stop [4]

%

%  bivariate/complex EMD options:

%

% COMPLEX_VERSION: selects the algorithm used for complex EMD ([3])

% COMPLEX_VERSION = 1: "algorithm 1"

% COMPLEX_VERSION = 2: "algorithm 2" (default)

% 

% NDIRS: number of directions in which envelopes are computed (default 4)

% rem: the actual number of directions (according to [3]) is 2*NDIRS

% 

%  other options:

%

% T: sampling times (line vector) (default: 1:length(x))

%

% MAXITERATIONS: maximum number of sifting iterations for the computation of each

% mode (default: 2000)

%

% MAXMODES: maximum number of imfs extracted (default: Inf)

%

% DISPLAY: if equals to 1 shows sifting steps with pause

% if equals to 2 shows sifting steps without pause (movie style)

% rem: display is disabled when the input is complex

%

% INTERP: interpolation scheme: 'linear', 'cubic', 'pchip' or 'spline' (default)

% see interp1 documentation for details

%

% MASK: masking signal used to improve the decomposition according to [5]

%

%

%   Examples

%

%

%X = rand(1,512);

%

%IMF = emd(X);

%

%IMF = emd(X,'STOP',[0.1,0.5,0.05],'MAXITERATIONS',100);

%

%T=linspace(0,20,1e3);

%X = 2*exp(i*T)+exp(3*i*T)+.5*T;

%IMF = emd(X,'T',T);

%

%OPTIONS.DISLPAY = 1;

%OPTIONS.FIX = 10;

%OPTIONS.MAXMODES = 3;

%[IMF,ORT,NBITS] = emd(X,OPTIONS);

%

%

%   References

%

%

% [1] N. E. Huang et al., "The empirical mode decomposition and the

% Hilbert spectrum for non-linear and non stationary time series analysis",

% Proc. Royal Soc. London A, Vol. 454, pp. 903-995, 1998

%

% [2] G. Rilling, P. Flandrin and P. Gon鏰lves

% "On Empirical Mode Decomposition and its algorithms",

% IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing

% NSIP-03, Grado (I), June 2003

%

% [3] G. Rilling, P. Flandrin, P. Gon鏰lves and J. M. Lilly.,

% "Bivariate Empirical Mode Decomposition",

% Signal Processing Letters (submitted)

%

% [4] N. E. Huang et al., "A confidence limit for the Empirical Mode

% Decomposition and Hilbert spectral analysis",

% Proc. Royal Soc. London A, Vol. 459, pp. 2317-2345, 2003

%

% [5] R. Deering and J. F. Kaiser, "The use of a masking signal to improve 

% empirical mode decomposition", ICASSP 2005

%

%

% See also

%  emd_visu (visualization),

%  emdc, emdc_fix (fast implementations of EMD),

%  cemdc, cemdc_fix, cemdc2, cemdc2_fix (fast implementations of bivariate EMD),

%  hhspectrum (Hilbert-Huang spectrum)

%

%

% G. Rilling, last modification: 3.2007

% [email protected]

function [imf,ort,nbits] = emd(varargin)

[x,t,sd,sd2,tol,MODE_COMPLEX,ndirs,display_sifting,sdt,sd2t,r,imf,k,nbit,NbIt,MAXITERATIONS,FIXE,FIXE_H,MAXMODES,INTERP,mask] = init(varargin{:});

if display_sifting

  fig_h = figure;

end

%main loop : requires at least 3 extrema to proceed

while (~stop_EMD(r,MODE_COMPLEX,ndirs) && (k < MAXMODES+1 || MAXMODES == 0) && ~any(mask))

  % current mode

  m = r;

  % mode at previous iteration

  mp = m;

  %computation of mean and stopping criterion

  if FIXE

    [stop_sift,moyenne] = stop_sifting_fixe(t,m,INTERP,MODE_COMPLEX,ndirs);

  elseif FIXE_H

    stop_count = 0;

    [stop_sift,moyenne] = stop_sifting_fixe_h(t,m,INTERP,stop_count,FIXE_H,MODE_COMPLEX,ndirs);

  else

    [stop_sift,moyenne] = stop_sifting(m,t,sd,sd2,tol,INTERP,MODE_COMPLEX,ndirs);

  end

  % in case the current mode is so small that machine precision can cause

  % spurious extrema to appear

  if (max(abs(m))) < (1e-10)*(max(abs(x)))

    if ~stop_sift

      warning('emd:warning','forced stop of EMD : too small amplitude')

    else

      disp('forced stop of EMD : too small amplitude')

    end

    break

  end

  % sifting loop

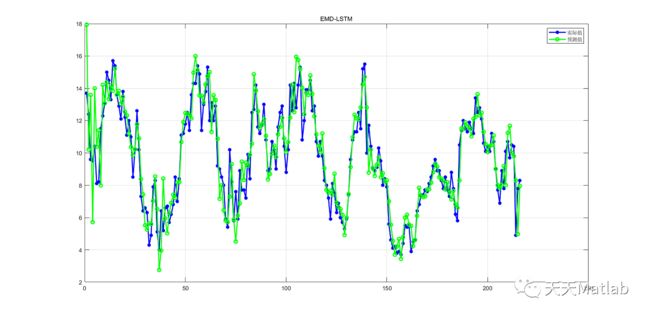
  while ~stop_sift && nbit

    if(~MODE_COMPLEX && nbit>MAXITERATIONS/5 && mod(nbit,floor(MAXITERATIONS/10))==0 && ~FIXE && nbit > 100)

      disp(['mode ',int2str(k),', iteration ',int2str(nbit)])

      if exist('s','var')

        disp(['stop parameter mean value : ',num2str(s)])

      end

      [im,iM] = extr(m);

      disp([int2str(sum(m(im) > 0)),' minima > 0; ',int2str(sum(m(iM) < 0)),' maxima < 0.'])

    end

    %sifting

    m = m - moyenne;

    %computation of mean and stopping criterion

    if FIXE

      [stop_sift,moyenne] = stop_sifting_fixe(t,m,INTERP,MODE_COMPLEX,ndirs);

    elseif FIXE_H

      [stop_sift,moyenne,stop_count] = stop_sifting_fixe_h(t,m,INTERP,stop_count,FIXE_H,MODE_COMPLEX,ndirs);

    else

      [stop_sift,moyenne,s] = stop_sifting(m,t,sd,sd2,tol,INTERP,MODE_COMPLEX,ndirs);

    end

    % display

    if display_sifting && ~MODE_COMPLEX

      NBSYM = 2;

      [indmin,indmax] = extr(mp);

      [tmin,tmax,mmin,mmax] = boundary_conditions(indmin,indmax,t,mp,mp,NBSYM);

      envminp = interp1(tmin,mmin,t,INTERP);

      envmaxp = interp1(tmax,mmax,t,INTERP);

      envmoyp = (envminp+envmaxp)/2;

      if FIXE || FIXE_H

        display_emd_fixe(t,m,mp,r,envminp,envmaxp,envmoyp,nbit,k,display_sifting)

      else

        sxp=2*(abs(envmoyp))./(abs(envmaxp-envminp));

        sp = mean(sxp);

        display_emd(t,m,mp,r,envminp,envmaxp,envmoyp,s,sp,sxp,sdt,sd2t,nbit,k,display_sifting,stop_sift)

      end

    end

    mp = m;

    nbit=nbit+1;

    NbIt=NbIt+1;

    if(nbit==(MAXITERATIONS-1) && ~FIXE && nbit > 100)

      if exist('s','var')

        warning('emd:warning',['forced stop of sifting : too many iterations... mode ',int2str(k),'. stop parameter mean value : ',num2str(s)])

      else

        warning('emd:warning',['forced stop of sifting : too many iterations... mode ',int2str(k),'.'])

      end

    end

  end % sifting loop

  imf(k,:) = m;

  if display_sifting

    disp(['mode ',int2str(k),' stored'])

  end

  nbits(k) = nbit;

  k = k+1;

  r = r - m;

  nbit=0;

end %main loop

if any(r) && ~any(mask)

  imf(k,:) = r;

end

ort = io(x,imf);

if display_sifting

  close

end

end

%---------------------------------------------------------------------------------------------------

% tests if there are enough (3) extrema to continue the decomposition

function stop = stop_EMD(r,MODE_COMPLEX,ndirs)

if MODE_COMPLEX

  for k = 1:ndirs

    phi = (k-1)*pi/ndirs;

    [indmin,indmax] = extr(real(exp(i*phi)*r));

    ner(k) = length(indmin) + length(indmax);

  end

  stop = any(ner < 3);

else

  [indmin,indmax] = extr(r);

  ner = length(indmin) + length(indmax);

  stop = ner < 3;

end

end

%---------------------------------------------------------------------------------------------------

% computes the mean of the envelopes and the mode amplitude estimate

function [envmoy,nem,nzm,amp] = mean_and_amplitude(m,t,INTERP,MODE_COMPLEX,ndirs)

NBSYM = 2;

if MODE_COMPLEX

  switch MODE_COMPLEX

    case 1

      for k = 1:ndirs

        phi = (k-1)*pi/ndirs;

        y = real(exp(-i*phi)*m);

        [indmin,indmax,indzer] = extr(y);

        nem(k) = length(indmin)+length(indmax);

        nzm(k) = length(indzer);

        [tmin,tmax,zmin,zmax] = boundary_conditions(indmin,indmax,t,y,m,NBSYM);

        envmin(k,:) = interp1(tmin,zmin,t,INTERP);

        envmax(k,:) = interp1(tmax,zmax,t,INTERP);

      end

      envmoy = mean((envmin+envmax)/2,1);

      if nargout > 3

        amp = mean(abs(envmax-envmin),1)/2;

      end

    case 2

      for k = 1:ndirs

        phi = (k-1)*pi/ndirs;

        y = real(exp(-i*phi)*m);

        [indmin,indmax,indzer] = extr(y);

        nem(k) = length(indmin)+length(indmax);

        nzm(k) = length(indzer);

        [tmin,tmax,zmin,zmax] = boundary_conditions(indmin,indmax,t,y,y,NBSYM);

        envmin(k,:) = exp(i*phi)*interp1(tmin,zmin,t,INTERP);

        envmax(k,:) = exp(i*phi)*interp1(tmax,zmax,t,INTERP);

      end

      envmoy = mean((envmin+envmax),1);

      if nargout > 3

        amp = mean(abs(envmax-envmin),1)/2;

      end

  end

else

  [indmin,indmax,indzer] = extr(m);

  nem = length(indmin)+length(indmax);

  nzm = length(indzer);

  [tmin,tmax,mmin,mmax] = boundary_conditions(indmin,indmax,t,m,m,NBSYM);

  envmin = interp1(tmin,mmin,t,INTERP);

  envmax = interp1(tmax,mmax,t,INTERP);

  envmoy = (envmin+envmax)/2;

  if nargout > 3

    amp = mean(abs(envmax-envmin),1)/2;

  end

end

end

%-------------------------------------------------------------------------------

% default stopping criterion

function [stop,envmoy,s] = stop_sifting(m,t,sd,sd2,tol,INTERP,MODE_COMPLEX,ndirs)

try

  [envmoy,nem,nzm,amp] = mean_and_amplitude(m,t,INTERP,MODE_COMPLEX,ndirs);

  sx = abs(envmoy)./amp;

  s = mean(sx);

  stop = ~((mean(sx > sd) > tol | any(sx > sd2)) & (all(nem > 2)));

  if ~MODE_COMPLEX

    stop = stop && ~(abs(nzm-nem)>1);

  end

catch

  stop = 1;

  envmoy = zeros(1,length(m));

  s = NaN;

end

end

%-------------------------------------------------------------------------------

% stopping criterion corresponding to option FIX

function [stop,moyenne]= stop_sifting_fixe(t,m,INTERP,MODE_COMPLEX,ndirs)

try

  moyenne = mean_and_amplitude(m,t,INTERP,MODE_COMPLEX,ndirs);

  stop = 0;

catch

  moyenne = zeros(1,length(m));

  stop = 1;

end

end

%-------------------------------------------------------------------------------

% stopping criterion corresponding to option FIX_H

function [stop,moyenne,stop_count]= stop_sifting_fixe_h(t,m,INTERP,stop_count,FIXE_H,MODE_COMPLEX,ndirs)

try

  [moyenne,nem,nzm] = mean_and_amplitude(m,t,INTERP,MODE_COMPLEX,ndirs);

  if (all(abs(nzm-nem)>1))

    stop = 0;

    stop_count = 0;

  else

    stop_count = stop_count+1;

    stop = (stop_count == FIXE_H);

  end

catch

  moyenne = zeros(1,length(m));

  stop = 1;

end

end

%-------------------------------------------------------------------------------

% displays the progression of the decomposition with the default stopping criterion

function display_emd(t,m,mp,r,envmin,envmax,envmoy,s,sb,sx,sdt,sd2t,nbit,k,display_sifting,stop_sift)

subplot(4,1,1)

plot(t,mp);hold on;

plot(t,envmax,'--k');plot(t,envmin,'--k');plot(t,envmoy,'r');

title(['IMF ',int2str(k),';   iteration ',int2str(nbit),' before sifting']);

set(gca,'XTick',[])

hold  off

subplot(4,1,2)

plot(t,sx)

hold on

plot(t,sdt,'--r')

plot(t,sd2t,':k')

title('stop parameter')

set(gca,'XTick',[])

hold off

subplot(4,1,3)

plot(t,m)

title(['IMF ',int2str(k),';   iteration ',int2str(nbit),' after sifting']);

set(gca,'XTick',[])

subplot(4,1,4);

plot(t,r-m)

title('residue');

disp(['stop parameter mean value : ',num2str(sb),' before sifting and ',num2str(s),' after'])

if stop_sift

  disp('last iteration for this mode')

end

if display_sifting == 2

  pause(0.01)

else

  pause

end

end

%---------------------------------------------------------------------------------------------------

% displays the progression of the decomposition with the FIX and FIX_H stopping criteria

function display_emd_fixe(t,m,mp,r,envmin,envmax,envmoy,nbit,k,display_sifting)

subplot(3,1,1)

plot(t,mp);hold on;

plot(t,envmax,'--k');plot(t,envmin,'--k');plot(t,envmoy,'r');

title(['IMF ',int2str(k),';   iteration ',int2str(nbit),' before sifting']);

set(gca,'XTick',[])

hold  off

subplot(3,1,2)

plot(t,m)

title(['IMF ',int2str(k),';   iteration ',int2str(nbit),' after sifting']);

set(gca,'XTick',[])

subplot(3,1,3);

plot(t,r-m)

title('residue');

if display_sifting == 2

  pause(0.01)

else

  pause

end

end

%---------------------------------------------------------------------------------------

% defines new extrema points to extend the interpolations at the edges of the

% signal (mainly mirror symmetry)

function [tmin,tmax,zmin,zmax] = boundary_conditions(indmin,indmax,t,x,z,nbsym)

lx = length(x);

if (length(indmin) + length(indmax) < 3)

error('not enough extrema')

end

    % boundary conditions for interpolations :

if indmax(1) < indmin(1)

     if x(1) > x(indmin(1))

lmax = fliplr(indmax(2:min(end,nbsym+1)));

lmin = fliplr(indmin(1:min(end,nbsym)));

lsym = indmax(1);

else

lmax = fliplr(indmax(1:min(end,nbsym)));

lmin = [fliplr(indmin(1:min(end,nbsym-1))),1];

lsym = 1;

end

else

if x(1) < x(indmax(1))

lmax = fliplr(indmax(1:min(end,nbsym)));

lmin = fliplr(indmin(2:min(end,nbsym+1)));

lsym = indmin(1);

else

lmax = [fliplr(indmax(1:min(end,nbsym-1))),1];

lmin = fliplr(indmin(1:min(end,nbsym)));

lsym = 1;

end

end

    

if indmax(end) < indmin(end)

if x(end) < x(indmax(end))

rmax = fliplr(indmax(max(end-nbsym+1,1):end));

rmin = fliplr(indmin(max(end-nbsym,1):end-1));

rsym = indmin(end);

else

rmax = [lx,fliplr(indmax(max(end-nbsym+2,1):end))];

rmin = fliplr(indmin(max(end-nbsym+1,1):end));

rsym = lx;

end

else

if x(end) > x(indmin(end))

rmax = fliplr(indmax(max(end-nbsym,1):end-1));

rmin = fliplr(indmin(max(end-nbsym+1,1):end));

rsym = indmax(end);

else

rmax = fliplr(indmax(max(end-nbsym+1,1):end));

rmin = [lx,fliplr(indmin(max(end-nbsym+2,1):end))];

rsym = lx;

end

end

    

tlmin = 2*t(lsym)-t(lmin);

tlmax = 2*t(lsym)-t(lmax);

trmin = 2*t(rsym)-t(rmin);

trmax = 2*t(rsym)-t(rmax);

    

% in case symmetrized parts do not extend enough

if tlmin(1) > t(1) || tlmax(1) > t(1)

if lsym == indmax(1)

lmax = fliplr(indmax(1:min(end,nbsym)));

else

lmin = fliplr(indmin(1:min(end,nbsym)));

end

if lsym == 1

error('bug')

end

lsym = 1;

tlmin = 2*t(lsym)-t(lmin);

tlmax = 2*t(lsym)-t(lmax);

end   

    

if trmin(end) < t(lx) || trmax(end) < t(lx)

if rsym == indmax(end)

rmax = fliplr(indmax(max(end-nbsym+1,1):end));

else

rmin = fliplr(indmin(max(end-nbsym+1,1):end));

end

if rsym == lx

error('bug')

end

rsym = lx;

trmin = 2*t(rsym)-t(rmin);

trmax = 2*t(rsym)-t(rmax);

end 

          

zlmax =z(lmax); 

zlmin =z(lmin);

zrmax =z(rmax); 

zrmin =z(rmin);

     

tmin = [tlmin t(indmin) trmin];

tmax = [tlmax t(indmax) trmax];

zmin = [zlmin z(indmin) zrmin];

zmax = [zlmax z(indmax) zrmax];

end

    

%---------------------------------------------------------------------------------------------------

%extracts the indices of extrema

function [indmin, indmax, indzer] = extr(x,t)

if(nargin==1)

  t=1:length(x);

end

m = length(x);

if nargout > 2

  x1=x(1:m-1);

  x2=x(2:m);

  indzer = find(x1.*x2<0);

  if any(x == 0)

    iz = find( x==0 );

    indz = [];

    if any(diff(iz)==1)

      zer = x == 0;

      dz = diff([0 zer 0]);

      debz = find(dz == 1);

      finz = find(dz == -1)-1;

      indz = round((debz+finz)/2);

    else

      indz = iz;

    end

    indzer = sort([indzer indz]);

  end

end

d = diff(x);

n = length(d);

d1 = d(1:n-1);

d2 = d(2:n);

indmin = find(d1.*d2<0 & d1<0)+1;

indmax = find(d1.*d2<0 & d1>0)+1;

% when two or more successive points have the same value we consider only one extremum in the middle of the constant area

% (only works if the signal is uniformly sampled)

if any(d==0)

  imax = [];

  imin = [];

  bad = (d==0);

  dd = diff([0 bad 0]);

  debs = find(dd == 1);

  fins = find(dd == -1);

  if debs(1) == 1

    if length(debs) > 1

      debs = debs(2:end);

      fins = fins(2:end);

    else

      debs = [];

      fins = [];

    end

  end

  if length(debs) > 0

    if fins(end) == m

      if length(debs) > 1

        debs = debs(1:(end-1));

        fins = fins(1:(end-1));

      else

        debs = [];

        fins = [];

      end

    end

  end

  lc = length(debs);

  if lc > 0

    for k = 1:lc

      if d(debs(k)-1) > 0

        if d(fins(k)) < 0

          imax = [imax round((fins(k)+debs(k))/2)];

        end

      else

        if d(fins(k)) > 0

          imin = [imin round((fins(k)+debs(k))/2)];

        end

      end

    end

  end

  if length(imax) > 0

    indmax = sort([indmax imax]);

  end

  if length(imin) > 0

    indmin = sort([indmin imin]);

  end

end

end

%---------------------------------------------------------------------------------------------------

function ort = io(x,imf)

% ort = IO(x,imf) computes the index of orthogonality

%

% inputs : - x    : analyzed signal

%          - imf  : empirical mode decomposition

n = size(imf,1);

s = 0;

for i = 1:n

  for j =1:n

    if i~=j

      s = s + abs(sum(imf(i,:).*conj(imf(j,:)))/sum(x.^2));

    end

  end

end

ort = 0.5*s;

end

%---------------------------------------------------------------------------------------------------

function [x,t,sd,sd2,tol,MODE_COMPLEX,ndirs,display_sifting,sdt,sd2t,r,imf,k,nbit,NbIt,MAXITERATIONS,FIXE,FIXE_H,MAXMODES,INTERP,mask] = init(varargin)

x = varargin{1};

if nargin == 2

  if isstruct(varargin{2})

    inopts = varargin{2};

  else

    error('when using 2 arguments the first one is the analyzed signal X and the second one is a struct object describing the options')

  end

elseif nargin > 2

  try

    inopts = struct(varargin{2:end});

  catch

    error('bad argument syntax')

  end

end

% default for stopping

defstop = [0.05,0.5,0.05];

opt_fields = {'t','stop','display','maxiterations','fix','maxmodes','interp','fix_h','mask','ndirs','complex_version'};

defopts.stop = defstop;

defopts.display = 0;

defopts.t = 1:max(size(x));

defopts.maxiterations = 2000;

defopts.fix = 0;

defopts.maxmodes = 0;

defopts.interp = 'spline';

defopts.fix_h = 0;

defopts.mask = 0;

defopts.ndirs = 4;

defopts.complex_version = 2;

opts = defopts;

if(nargin==1)

  inopts = defopts;

elseif nargin == 0

  error('not enough arguments')

end

names = fieldnames(inopts);

for nom = names'

  if ~any(strcmpi(char(nom), opt_fields))

    error(['bad option field name: ',char(nom)])

  end

  if ~isempty(eval(['inopts.',char(nom)])) % empty values are discarded

    eval(['opts.',lower(char(nom)),' = inopts.',char(nom),';'])

  end

end

t = opts.t;

stop = opts.stop;

display_sifting = opts.display;

MAXITERATIONS = opts.maxiterations;

FIXE = opts.fix;

MAXMODES = opts.maxmodes;

INTERP = opts.interp;

FIXE_H = opts.fix_h;

mask = opts.mask;

ndirs = opts.ndirs;

complex_version = opts.complex_version;

if ~isvector(x)

  error('X must have only one row or one column')

end

if size(x,1) > 1

  x = x.';

end

if ~isvector(t)

  error('option field T must have only one row or one column')

end

if ~isreal(t)

  error('time instants T must be a real vector')

end

if size(t,1) > 1

  t = t';

end

if (length(t)~=length(x))

  error('X and option field T must have the same length')

end

if ~isvector(stop) || length(stop) > 3

  error('option field STOP must have only one row or one column of max three elements')

end

if ~all(isfinite(x))

  error('data elements must be finite')

end

if size(stop,1) > 1

  stop = stop';

end

L = length(stop);

if L < 3

  stop(3)=defstop(3);

end

if L < 2

  stop(2)=defstop(2);

end

if ~ischar(INTERP) || ~any(strcmpi(INTERP,{'linear','cubic','spline'}))

  error('INTERP field must be ''linear'', ''cubic'', ''pchip'' or ''spline''')

end

%special procedure when a masking signal is specified

if any(mask)

  if ~isvector(mask) || length(mask) ~= length(x)

    error('masking signal must have the same dimension as the analyzed signal X')

  end

  if size(mask,1) > 1

    mask = mask.';

  end

  opts.mask = 0;

  imf1 = emd(x+mask,opts);

  imf2 = emd(x-mask,opts);

  if size(imf1,1) ~= size(imf2,1)

    warning('emd:warning',['the two sets of IMFs have different sizes: ',int2str(size(imf1,1)),' and ',int2str(size(imf2,1)),' IMFs.'])

  end

  S1 = size(imf1,1);

  S2 = size(imf2,1);

  if S1 ~= S2

    if S1 < S2

      tmp = imf1;

      imf1 = imf2;

      imf2 = tmp;

    end

    imf2(max(S1,S2),1) = 0;

  end

  imf = (imf1+imf2)/2;

end

sd = stop(1);

sd2 = stop(2);

tol = stop(3);

lx = length(x);

sdt = sd*ones(1,lx);

sd2t = sd2*ones(1,lx);

if FIXE

  MAXITERATIONS = FIXE;

  if FIXE_H

    error('cannot use both ''FIX'' and ''FIX_H'' modes')

  end

end

MODE_COMPLEX = ~isreal(x)*complex_version;

if MODE_COMPLEX && complex_version ~= 1 && complex_version ~= 2

  error('COMPLEX_VERSION parameter must equal 1 or 2')

end

% number of extrema and zero-crossings in residual

ner = lx;

nzr = lx;

r = x;

if ~any(mask) % if a masking signal is specified "imf" already exists at this stage

  imf = [];

end

k = 1;

% iterations counter for extraction of 1 mode

nbit=0;

% total iterations counter

NbIt=0;

end

%---------------------------------------------------------------------------------------------------

⛄ 运行结果

⛄ 参考文献

[1]王亦斌、孙涛、梁雪春、谢海洋. “基于EMD-LSTM模型的河水量水位预测。” 水利水电科技进展 40.6(2020):8.

⛄ Matlab代码关注

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料