IS ATTENTION BETTER THAN MATRIX DECOMPOSITION

IS ATTENTION BETTER THAN MATRIX DECOMPOSITION?

原始论文：Is Attention Better Than Matrix Decomposition? | OpenReview

代码：[Gsunshine/Enjoy-Hamburger: ICLR 2021 top 3%] Is Attention Better Than Matrix Decomposition? (github.com)

摘要

目前self-attention机制已经在深度学习领域发挥着至关重要的作用。在建模全局信息时，attention机制是不是能够被取代，或者有更好的方法？作者发现在编码长距离依赖性能和计算成本方面，self-attention并不比20年前的矩阵分解（Matrix decomposition）效果好。作者建模全局信息问题转化为一个低秩补全问题（low-rank completion problem），使用优化算法帮助设计全局信息块。论文提出了一系列的Hamburger结构，作者利用优化方法来求解矩阵分解问题，将输入表示分解为子矩阵，并重构低秩嵌入。当仔细处理矩阵分解反向传播的梯度时，具有不同矩阵分解的Hamburger结构在对全局上下文模块建模过程中比self-attention表现更好。在视觉任务中进行了全面实验，其中学习全局上下文至关重要，包括语义分割和图像生成，证明了对自我注意及其变体的显著改进。

1、简介

本文聚焦于设计一个全局信息模块方法。

作者在基础视觉任务（语义分割、图像生成）展示了Hamburger模型在全局信息的获取上具有的优势。实验证明，优化设计的Hamburger在避免MD迭代计算图反向传播的不稳定梯度时，可以与最先进的注意力模型竞争。Hamburger刷新的几个语义分割数据集的最新记录，实验证明了它的有效性。

作者在这篇文章的主要贡献：

1. 作者展示了一种设计全局信息块的白盒(white-box)方法，即通过将最小化目标函数的优化算法转化为体系结构，在该优化算法中，将全局相关性建模为低秩补全问题。
2. 作者提出了Hamburger结构，一个轻量，但能捕捉全局信息的模块，具有$O(n)$的时间复杂度，在语义分割和图像生成中胜过了很多attention及其变体。
3. 通过迭代优化算法，我们发现在网络中应用MD的主要障碍是不稳定的后向梯度。作为一种实用的解决方案，所提出的一步梯度有助于Hamburger的MD的训练。

2、方法

2.1 矩阵分解原理

矩阵分解在Hamburger结构中至关重要。一种常见的观点是，矩阵分解将观察到的矩阵分解为几个子矩阵的乘积，例如奇异值分解(Singular Value Decomposition, SVD)。然而，更具启发性的观点是，通过假设生成过程，矩阵分解充当生成的逆过程，分解组成复杂数据的原子。从原始矩阵的重构中，矩阵分解恢复了观测数据的潜在结构。

假设给定的数据被排列为一个大矩阵的列$X=[x_1,...,x_n]\in R^{d\times n}$。一般的假设是$X$中隐藏着一个低维子空间，或多个子空间的并集。这里存在一个字典矩阵$D=[d_1,...,d_r]\in R_{d\times r}$，对应编码$C=[c_1,...,c_n]\in R^{r\times n}$，则矩阵$X$可以按照如下表示：
$$X=\overline{X}+E=DC+E$$
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uEnyovXt-1667984059347)(C:\Users\xiehou\AppData\Roaming\Typora\typora-user-images\image-20221106021820265.png)]

其中$\overline{X}\in R^{d\times n}$是一个低秩输出重构，$E\in R^{d\times n}$是一个噪声矩阵，可以被丢弃。作者假设还原矩阵$\overline{X}$应该具有低秩的特性，如下所示：
$$rank(\overline{X})\le min(rank(D),rank(C))\le r\ll min(d,n)$$
不同的矩阵分解将会分解出不同的矩阵$D,C$和$E$。

2.2 方法提出

我们专注于为网络构建全局信息模块，无需精心的手工设计。

attention的工作原理如下：
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d}})V$$
其中矩阵$Q,K,V\in R^{n\times d}$是输入通过线性转化的特征映射，self-attention机制是通过一次性处理全部的token，而不像循环神经网络(RNN)一样逐个处理。

尽管self-attention及其变体取得了很大的成功，但是研究者仍然面临着两个问题(1) 基于self-attention开发一个新的全局信息捕捉模块，这是一个典型的手工设计过程；(2) 当前attention模块的可解释性。本文绕过了这两个问题，找到了一种通过定义良好的白盒(white-box)工具轻松设计全局上下文模块的方法。我们试图将人类归纳偏差（如全局上下文）作为目标函数，并使用优化算法来解决这样的问题，以设计模块的架构。优化算法创建一个计算图，接受一些输入，并最终输出解决方案。我们将优化算法的计算图应用于上下文模块的中心部分。

基于上述方法，我们需要建模网络的全局信息问题作为一个优化问题。采用一个卷积神经网络（CNN）作为一个实例来进行长远的讨论。网络输入一张图像后，输出一个tensor $\chi \in R^{C\times H\times W}$。这个tensor将被看成一组$HWC$维超像素，将张量进行展开成一个矩阵$X\in R^{C\times HW}$。当这个模块学习长序列依赖或者全局信息时，这个隐藏的假设是超像素内在的相关性。为了简单起见，我们假设超像素是线性相关的，这意味着$X$中的每个超像素可以表示为元素通常远小于$HW$的线性组合。在理想的环境下，隐藏在$X$中的全局信息可以是低秩的。然而卷积神经网络很难学习到全局信息，学习$X$经常会被冗余信息和不完整性破坏。通过上述的分析可以通过一个潜在的方式去建模全局信息，将$X$分解成低秩的$\overline{X}$和应该被抛弃的冗余噪声$E$，具体如上式(1)矩阵分解的形式，它将同时过滤掉冗余信息和不兼容信息。矩阵分解的目标函数如下式所示：
KaTeX parse error: Limit controls must follow a math operator at position 11: M={\min} \̲l̲i̲m̲i̲t̲s̲_{D,C} \ L(X,D…
其中$L$代表的是重构损失，$R_1$和$R_2$是$D$和$C$的正则项。公式(4)就是我们最终的目标函数，我们使用矩阵分解解决了反向传播的梯度问题。

2.2.1 hamburger模型

hamburger模型结构如上图1所示，中间层(ham)是矩阵分解，上下两层(bread)是线性变化层。顾名思义，hamburger模块的输入特征$Z\in R^{d_z\times n}$进入一个线性变化$W_l\in R^{d\times d_z}$的特征空间，叫做“lower bread”，然后使用矩阵分解$M$去解决低秩信号子空间，对应的是“ham”，最后用另外一个线性变化$W_u\in R^{d_z\times d}$将提取的信号转化为输出，叫做"upper bread"。
$$H(Z)=W_{u}M(W_{l}Z)$$
其中$M$是矩阵分解，目的是恢复清晰的潜在结构，起全局非线性的作用。通过图一，最终的输出可以如下所式进行计算得出：
$$Y=Z+BN(H(Z))$$
$BN$是Batch Normailzation。

2.2.2 Hams

矩阵分解$M$的输入是“lower bread”的输出，输出是低秩的重构矩阵，简要如下所示：
$$M(x)=\overline{X}=DC$$
作者共调研了两种矩阵分解方法，分别是Vector Quantization(VQ)和Non-negative Matrix Factorization(NMF)去求解$D、C$，并且重构$\overline{X}$，Concept Decomposition(CD)，概念分解。

Vector Quantization：矢量量化，是一种典型的数据压缩算法，可以用矩阵分解的形式来表示一个优化算法：
$$\underset{D,C}{\min }\parallel X-DC{\parallel }_{F}s.t.c_i\in \{e_1,e_2,...,e_r\}$$
其中$e_i$是正则单位/基向量，$[0,...,\underset{ith}{1},...,0]$。使用Kmeans算法去最小化公式8这个目标函数。为了确保$VQ$是可微分的，作者将$\arg \min$和Euclidean distance(欧式距离)使用softmax和cosine相似度进行替换，具体如算法1所示。其中$cosine(D,X)$是一个相似矩阵，全部满足$cosine(D,X{)}_{ij}=\frac{d_i^T{x}_j}{\parallel d\parallel \parallel x\parallel }$

Non-negative Matrix Factorization: 非负矩阵分解，如果对$D$和$C$添加非负约束，则会导致NMF：
$$\underset{D,C}{\min }\parallel X-DC{\parallel }_{F}s.t.D_{ij}\ge 0,C_{jk}\ge 0$$
为了满足非负的约束，在将$X$输入到NMF前我们添加了ReLU非线性约束，使用算法2来对NMF进行求解，这保证了算法的收敛性。

对于white-box全局信息模块，VQ、CD和NMF算法是简明轻量的，也展示了显著的效果。他们的时间复杂度是$O(ndr)$，self-attention的时间复杂度是$O(n^{2}d)$，但是$r\ll n$。矩阵分解的方法都是内存有好的，它们大量避免了大的$n\times n$的矩阵作为中间变量。

2.3 One-step Gradient

算法$M$是一个计算图的优化算法，将其融合到网络中的关键是迭代算法如何融入到梯度下降算法中。类似于RNN的优化行为表明，通过时间反向传播BPTT(Back-Propagation Through Time)算法是区分迭代过程的标准选择。然而，实际上BPTT不稳定的梯度损害了Hamburger的表现效果。因此，作者建立了一个抽象模型来分析BPTT的缺点，并且考虑矩阵分解作为一个优化问题，尝试发现一个实用的解决方案。

图2展现了一个算法的更新过程，其中$x,y,h^t$分别表示输入、输出和时间$t$的中间结果。$F,G$代表的是函数操作。每一个时间步，模型将会收到一个相同的输入$x$。
$$h^{t+1}=F(h^t,x)$$
所有的中间过程$h^i$将会被丢弃。仅有最后一步$h^t$将会通过函数$G$输出为$y$.
$$y=G(h^t)$$
在这个BPTT算法中，这个输出$y$从输入$x$均被给定，依照链式法则进行计算：
$$\frac{\partial y}{\partial x}=\sum _{i=0}^{t-1}\frac{\partial y}{\partial h^t}(\prod _{j=t-i}^{t-1}\frac{\partial h^{j-1}}{\partial h^j})\frac{\partial h^{t-i}}{\partial x}$$

当$L_h,h_0$接近于0时，很容易出现梯度消失现象；$x,L_h$接近于1时，很容易出现梯度爆炸。以下开始没看懂了：

3 实验

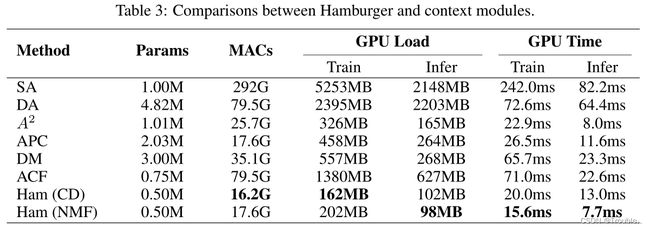
Hamburger和self-attention在建模在全局上下文上，具有性能和计算成本方面的优势。

消融实验：

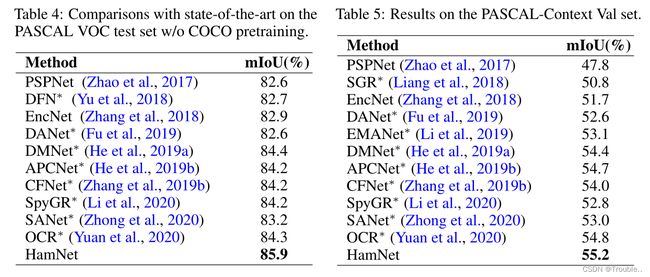
实验效果：

4 总结

本文研究了网络中的长程依赖建模。我们将学习全球背景描述为一个低秩补全问题。受这样一个低秩形式的启发，我们基于研究良好的矩阵分解模型开发了Hamburger Module。通过专门化矩阵分解的目标函数，由其优化算法创建的计算图自然定义了Hamburger的核心架构“ham”。Hamburger通过去噪和填充输入来学习可解释的全局上下文，并提高频谱的集中度。令人惊讶的是，当谨慎地处理后向梯度时，即使是20年前提出的简单矩阵分解，在挑战视觉任务语义分割和图像生成方面也与自我关注一样强大，而且轻便、快速、高效。我们计划通过整合位置信息和设计类似Transformer的解码器，将Hamburger扩展到自然语言处理，为一步梯度技巧奠定理论基础，或找到更好的方法来区分MD，并在未来提出高级MD。

参考文献

Enjoy Hamburger：注意力机制比矩阵分解更好吗？(I) - 知乎 (zhihu.com)

Enjoy Hamburger：注意力机制比矩阵分解更好吗？(II) - 知乎 (zhihu.com)

Enjoy Hamburger：注意力机制比矩阵分解更好吗？(III) - 知乎 (zhihu.com)