机器学习算法基础 Day6
回归算法-线性回归分析
回归:目标值连续
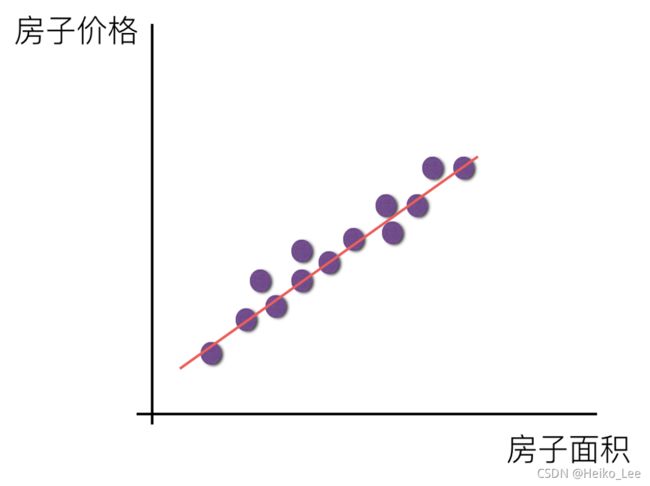
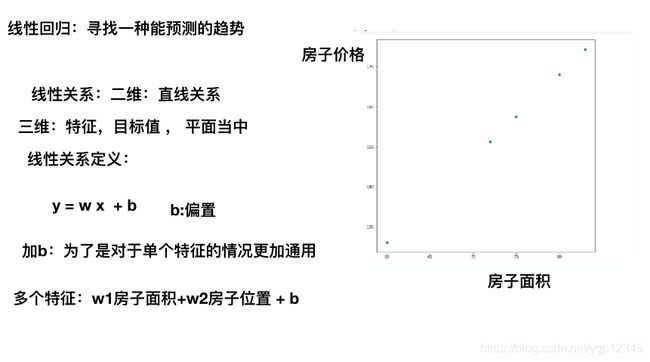
线性回归:寻找一种能预测的趋势
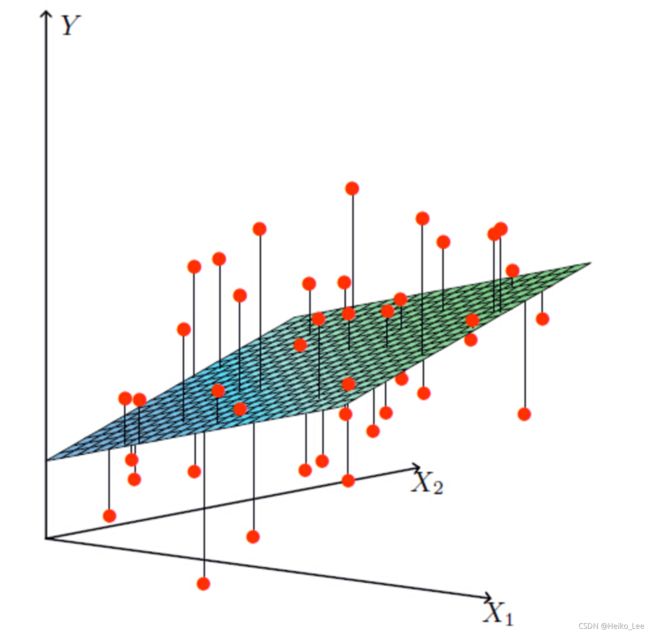
线性关系:二维,直线关系;三维,目标值在一个平面内。
线性模型
b是为了将平面的直线都概括进去。因为y=kx只能概括经过原点的直线
线性回归
通过属性的线性组合来进行预测的函数:
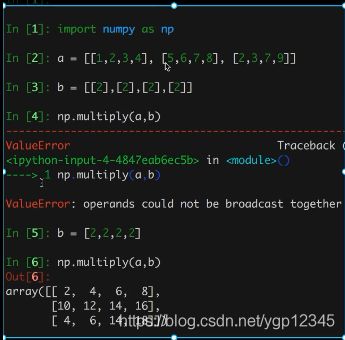
矩阵和数组的关系补充:
从上图分析,数组在numpy中是ndarray类型,我们引入矩阵,就是为了满足一些特定的运算,我们要求他必须是二维,二维是个什么概念?就是[[],[],[],[]]这种,就是深度为2,我们把特征值都搞成矩阵,当然权重也要搞成矩阵,因为目标值必须是一个样本对应一个值,如特征值的矩阵为1x4,那么权重矩阵就要4x1,这才能得到一个单独的数!!!下面演示一下之前numpy里疑惑的地方!
之前numpy就解释过multiple和dot方法,现在应该知道为什么二者不一样了,multiple针对数组,dot针对矩阵!
损失函数(误差大小)
预测结果与真实值是有一定的误差
单变量
多变量:
hw就是w0+w1x1+w2x2+…,要想求损失函数的值,就得算各个hw,要想知道hw,就得直到各个w的值。 尽量去减少这个损失(两种方式),目的是找到最小损失对应的W值。
下面提供两个方法去寻找最合适的w。
正规方程:
最小二乘法之正规方程(参数最优解)
这个参数向量,就可以让代价函数取最小值。
从上图我们可以直到正规方程完全利用线性代数的知识,当矩阵变得很复杂数据量很多的时候,正规方程就力不从心了。
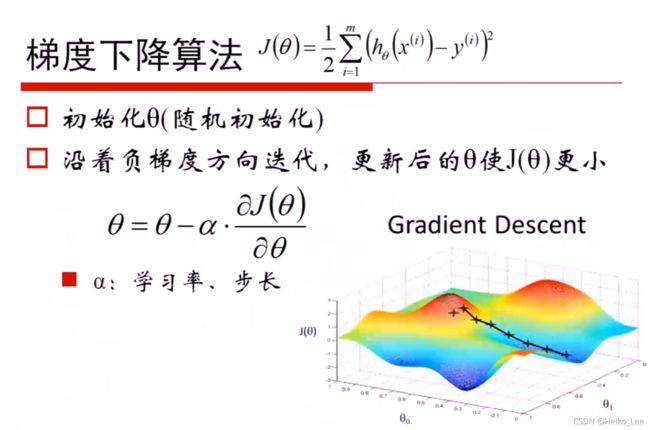
梯度下降法
这是另一种求w的方法
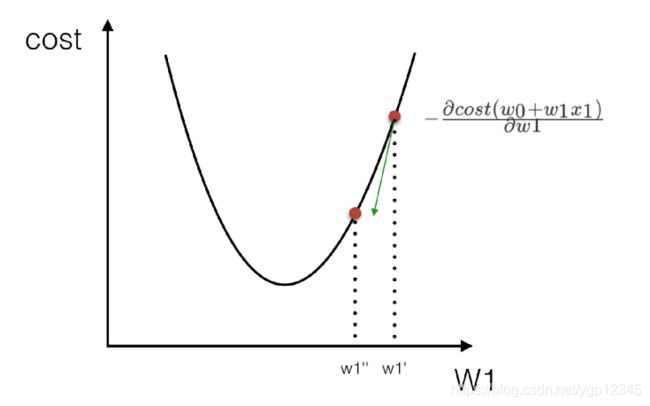
根据上图,我想说的是表示方向的那一坨表达式就是决定往哪个方向下降,而α是学习率,表示我每次下降多少?我们可以看一下下面这张图!
也就是我原先在这个曲面的某一点,然后我要想个办法去最低点,首先我要确定放向,也就是路线,我要咋个走才能到最低点,学习率是我要走多少步,我可以就走一步,但可能走过了,我可以一小步一小步的走,刚好走到最低点。
正规方程与梯度下降的对比?
正规方程适合数据量少的时候,正规方程是通过矩阵运算直接找到最低点,而梯度下降适合大数据,是个迭代过程,一点一点去找。
sklearn线性回归正规方程、梯度下降API
正规方程:
sklearn.linear_model.LinearRegression
梯度下降:
sklearn.linear_model.SGDRegressor线性回归实例
波士顿房价数据集分析流程
1、波士顿地区房价数据获取
2、波士顿地区房价数据分割
3、训练与测试数据标准化处理
4、使用最简单的线性回归模型LinearRegression和
梯度下降估计SGDRegressor对房价进行预测
def mylinear():
"""
线性回归直接预测房子价格
:return: None
"""
# 获取数据
lb = load_boston()
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
print(y_train, y_test)
# 特征值和目标值是都必须进行标准化处理, 列数不同,所以要实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# estimator预测
# 正规方程求解方式预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print(lr.coef_)
# 预测测试集的房子价格
y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
print("正规方程测试集里面每个房子的预测价格:", y_lr_predict)
print("正规方程的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
return None
回归性能评估
均方误差API:
sklearn.metrics.mean_squared_error
- mean_squared_error(y_true, y_pred)
均方误差回归损失
y_true:真实值
y_pred:预测值
return:浮点数结果
注:真实值,预测值为标准化之前的值
为什么要标准化之前的值?首先我们在计算h=w10+w1x1+…的时候,如果特征xi过大或太小,对h的影响很大,所以我们要进行标准化去计算,然后计算完后评估时,我不能拿标准化的数据去评估,这样并没有什么意义!
LinearRegression与SGDRegressor评估
线性回归器是最为简单、易用的回归模型。
从某种程度上限制了使用,尽管如此,在不知道特征之间关系的前提下,我们仍然使用线性回归器作为大多数系统的首要选择。
小规模数据:LinearRegression(不能解决拟合问题)以及其它
大规模数据:SGDRegressor
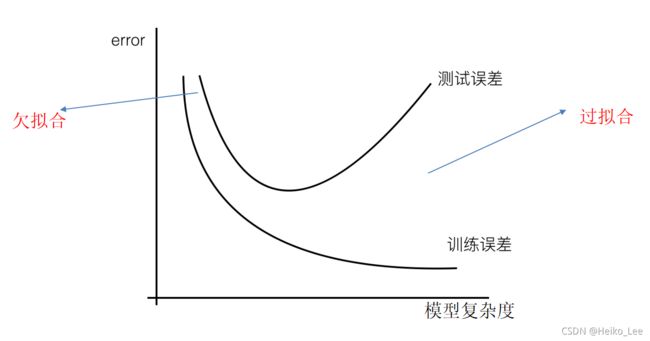
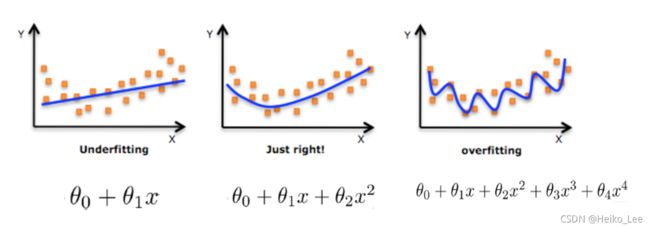
过拟合与欠拟合
分析上图1
分析上图2
训练数据训练很好,误差不大,为什么在测试集上面会有问题
过拟合:一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在训练数据外的数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
欠拟合:一个假设在训练数据上不能获得更好的拟合, 但是在训练数据外的数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
对线性模型进行训练学习会变成复杂模型
欠拟合原因以及解决办法
原因:
学习到数据的特征过少
解决办法:
增加数据的特征数量
过拟合原因以及解决办法
原因:
原始特征过多,存在一些嘈杂特征,
模型过于复杂是因为模型尝试去兼顾
各个测试数据点
解决办法:
进行特征选择,消除关联性大的特征(很难做)
交叉验证(让所有数据都有过训练)
正则化(了解)
L2正则化
作用:可以使得W的每个元素都很小,都接近于0
优点:越小的参数说明模型越简单,越简单的模型则越不
容易产生过拟合现象
线性回归为了把训练集数据表现得更好,容易出现过拟合
L2正则化:Ridge:岭回归-带有正则化的线性回归
带有正则化的线性回归-Ridge岭回归
sklearn.linear_model.Ridge- sklearn.linear_model.Ridge(alpha=1.0)
具有L2正则化的线性最小二乘法
alpha:正则化力度
coef_:回归系数
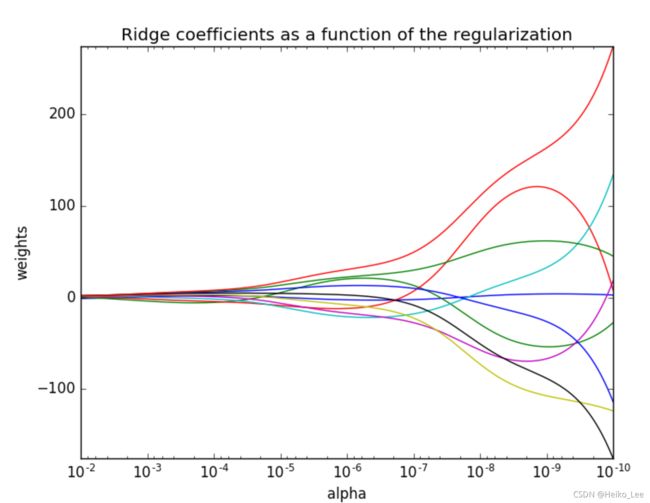
观察正则化程度的变化,对结果的影响?
答:正则化力度越大,权重系数越小!我们可以看到正则化力度越强,w越趋近于零!
线性回归 LinearRegression与Ridge对比
岭回归:回归得到的回归系数更符合实际,更可靠。另外,能让估计参数的波动范围变小,变的更稳定。在存在病态数据偏多的研究中有较大的实用价值。
def mylinear():
"""
线性回归直接预测房子价格
:return: None
"""
# 获取数据
lb = load_boston()
# 分割数据集到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
print(y_train, y_test)
# 特征值和目标值是都必须进行标准化处理, 列数不同,所以要实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.transform(y_test.reshape(-1, 1))
# 岭回归去进行房价预测
rd = Ridge(alpha=1.0)
rd.fit(x_train, y_train)
print(rd.coef_)
# 预测测试集的房子价格
y_rd_predict = std_y.inverse_transform(rd.predict(x_test))
print("岭回归测试集里面每个房子的预测价格:", y_rd_predict)
print("岭回归的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_rd_predict))
return None