李弘毅机器学习笔记：第十五章—半监督学习

监督学习和半监督学习

在supervised里面，你就是有一大推的training data，这些training data的组成是一个function的input跟output，假设你有R笔train data，每一笔train data有$x^r$,${\hat{y}}^r$。假设$x^r$是一张image，$\hat{y}$是class label。semi-supervised learning是在label上面，是有另外一组unlabel的data，这组data记做$x^u$,这组data只有input，没有output(U笔data)。在做semi-superised learning时，U远远大于R(unlabel的数量远远大于label data的数量)。semi-surprised learning可以分成两种，一种是transductive learning，一种是inductive learning。这两种最简单的分法是：在做transductive的时候，你的unlabel data就是你的testing data，inductive learning 就是说：不把unlabel data考虑进来。

为什么做semi-supervised learning，因为有人常会说，我们缺data，其实我们不是缺data，其实我们缺的是与label的data。比如说，你收集image很容易(在街上一直照就行了)，但是这些image是没有的label。label data 是很少的，unlabel是非常多的。所以semi-surprvised learning如果可以利用这些unlabel data来做某些事是会很有价值的。

我们人类可能一直是在semi-supervised learning，比如说，小孩子会从父母那边得到一点点的supervised(小孩子在街上，问爸爸妈妈这是什么，爸爸妈妈说：这是狗。在以后的日子里，小孩子会看到很多奇奇怪怪的东西，也没有人在告诉这是什么动物，但小孩子依然还是会判别出狗)

半监督学习的好处

为什么semi-supervised learning有可能会带来帮助呢？假设我们现在要做分类的task，建一个猫跟狗的classifier，我们同时有一大堆猫跟狗的图片。这些图片是没有label的，并不知道哪些是猫哪些是狗。

那今天我们只考虑有label的猫跟狗的data，画一个boundary，将猫跟狗的train data分开的话，你可能就会画在中间(垂直)。那如果unlabel的分布长的像灰色的点这个样子的话，这可能会影响你的决定。虽然unlabel data只告诉我们了input，但unlabeled data的分布可以告诉我们一些事。那你可能会把boundary变为这样(斜线)。但是semi-supervised learning使用unlabel的方式往往伴随着一些假设，其实semi-supervised learning有没有用，是取决于你这个假设符不符合实际/精不精确。

这边要讲四件事，第一个是在generative model的时候，怎么用semi-supervised learning。还要讲两个还蛮通用的假设，一个是Low-density Separation Assumption,另一个是Smoothness Assumption，最后还有Better Representation

监督生成模型和半监督生成模型

监督生成模型

我们都已经看过，supervised generative model，在supervised learning里面有一堆train example，你知道分别是属于class1，class2。你会去估测class1，class2的probability($P(X|C_i)$)

假设每一个class它的分布都是一个Gaussion distribution，那你会估测说class1是从μ是${\mu }^1$，covariance是$\Sigma$的Gaussion估测出来的，class2是从μ是${\mu }^2$，covariance是$\Sigma$的Gaussion估测出来的。

那现在有了这些probability，有了这些$\mu$、covariance，你就可以估测given一个新的data做classification，然后你就会决定boundary的位置在哪里。

半监督生成模型

但是今天给了我们一些unlabel data，它就会影响你的决定。举例来说，我们看左边这笔data，我们假设绿色这些使unlabel data，那如果你的$\mu$跟variance是${\mu }^1$,${\mu }^2,\Sigma$显然是不合理的。今天这个$\Sigma$应该比较接近圆圈，或者说你在sample的时候有点问题，所以你sample出比较奇怪的distribution。比如说，这两个class label data是比较多的(可能class2是比较多的，所以这边probability是比较大的)，总之看这些unlabel data以后，会影响你对probability，$\mu$,$\Sigma$的估测，就影响你的probability的式子，就影响了你的decision boundary。

对于实际过程中的做法，我们先讲操作方式，再讲原理。先初始化参数(class1,class2的几率，${\mu }^1$,${\mu }^2,\Sigma$，这些值，你可以用已经有label data先估测一个值，得到一组初始化的参数，这些参数统称$\theta$

• Step1 先计算每一笔unlabel data的 posterior probability，根据现有的$\theta$计算每一笔unlabel data属于class1的几率，那这个几率算出来是怎么样的是和你的model的值有关的。

• Step2 算出这个几率以后呢，你就可以update你的model，这个update的式子是非常的直觉，这个$C_1$的probability是怎么算呢，原来的没有unlabel data的时候，你的计算方法可能是：这个N是所有的example,$N_1$是被标注的$C_1$example，如果你要算$C_1$的probability，这件事情太直觉了，如果不考虑unlabel data的话(感觉就是$N_1$除以N)。但是现在我们要考虑unlabel data，那根据unlabel告诉我们的咨询，$C_1$是出现次数就是所有unlabel data它是$C_1$posterior probability的和。所有unlabel data而是根据它的posterior probability决定它有百分之多少是属于$C_1$,有多少是属于$C_2$，${\mu }^1$怎么算呢，原来不考虑unlabel data时，${\mu }^1$就是把所有$C_1$的label data都平均起来就结束了。如果今天加上unlabel data的话，其实就是把unlabel data的每一笔data$x^u$根据它的posterior probability做相乘。如果这个$x^u$比较偏向class1$C^1$的话，它对class1的影响就大一点，反之就小一点。(不用解释这是为什么这样，因为这太直觉了)$C_2$的 probability就是这样的做的${\mu }^1,{\mu }^2,\sum$也都是这样做的，有了新的model，你就会做step1，有了新的model以后，这个几率就不一样了，这个几率不一样了，在做step2，你的model就不一样了。这样update你的几率，然后就反复反复的下去。理论上这个方法会保证收敛，但是它的初始值跟GD会影响你收敛的结果。

这里的Step1就是Estep，而Step2就是Mstep（也就是熟悉的EM算法）

我们现在来解释下为什么这样做的：想法是这样子的。假设我们有原来的label data的时候，我们要做的事情是maximum likehood，每一笔train data 它的likehood是可以算出来的。把所有的 log likehood加起来就是log total loss。然后去maximum。那今天是unlabel data的话今天是不一样的。unlabel data我们并不知道它是来自哪一个class，我们咋样去估测它的几率呢。那我们说一笔unlabel data$x^u$出现的几率(我不知道它是从claas1还是class2来的，所以class1，class2都有可能)就是它在$C_1$的posterior probability跟$C_1$这个class产生这笔unlabel data的几率加上$C_2$的posterior probability乘以$C_2$这个class产生这笔unlabel data的几率。把他们通通合起来，就是这笔unlabel data产生的几率。

接下来要做事情就是maximum这件事情。但是由于不是凸函数，所以你要去iteratively solve这个函数

假设一：Low-density Separation

那接下来我们讲一个general的方式，这边基于的假设是Low-density Separation，也就是说：这个世界非黑即白的。什么是非黑即白呢？非黑即白意思就是说：假设我们现在有一大堆的data(有label data，也有unlabel data)，在两个class之间会有一个非常明显的红色boundary。比如说：现在两边都是label data，boundary 的话这两条直线都是可以的，就可以把这两个class分开，在train data上都是100%。但是你考虑unlabel data的话，左边的boundary是比较好的，右边的boundary是不好的。因为这个假设是基于这个世界是一个非黑即白的世界，这两个类之间会有一个很明显的界限。Low-density separation意思就是说，在这两个class交界处，density是比较低的。

Self-training

Low-density separation最简单的方法是self-training。self-training就是说，我们有一些label data并且还有一些unlabel data。接下来从label data中去train一个model，这个model叫做$f^{\ast }$,根据这个$f^{\ast }$去label你的unlabel data。你就把$x^u$丢进$f^{\ast }$,看它吐出来的$y^u$是什么，那就是你的label data。那这个叫做pseudo-label。那接下来你要从你的unlabel data set中拿出一些data，把它加到labeled data set里面。然后再回头去train你的$f^{\ast }$

在做regression时是不能用这一招的，主要因为把unlabeled data加入到训练数据中，$f^{\ast }$并不会受影响

你可能会觉得slef-training它很像是我们刚才generative model里面用的那个方法。他们唯一的差别就是在做self-training的时候，你用的是hard label；你在做generative mode时，你用的是soft model。在做self-training的时候我们会强制一笔train data是属于某一个class，但是在generative model的时候，根据它的posterior probability 它有一部分是属于class1一部分是属于class2。那到底哪一个比较好呢？那如果我们今天考虑的neural network的话，你可以比较看看哪一个方法比较好。

假设我们用neural network，你从你的 label data得到一笔network parameter(${\theta }^{\ast }$)。现在有一笔unlabel data$x^u$，根据参数${\theta }^{\ast }$分为两类(0.7的几率是class1,0.3的几率是class2)。如果是hard label的话，你就把它直接label成class1，所以$x^u$新的target第一维是1第二维是0(拿$x^u$train neural network)。如果去做soft的话。70 percent是属于class1,30percent是属于class2，那新的target是0.7跟0.3。在neural network中，这两个方法你觉得哪个是有用的呢，soft这个方法是没有用的，一定要用hard label。因为本来输出就是0.7和0.3，目标又设成0.7和0.3，相当于自己证明自己，所以没用。但我们用hard label 是什么意思呢？我们用hard label的时候，就是用low-density separation的概念。也就是说：今天我们看$x^u$它属于class1的几率只是比较高而已，我们没有很确定它一定是属于class1的，但这是一个非黑即白的世界，如果你看起来有点像class1，那就一定是class1。本来根据我的model说：0.7是class1 0.3是class2，那用hard label(low-density-separation)就改成它属于class1的几率是1(完全就不可能是class2)。soft是不会work的。

基于熵的正则化

刚才那一招有进阶版是“Entropy-based Regularization”。如果你用neural network，你的output是一个distribution，那我们不要限制说这个output一定要是class1、class2，但是我们做的假设是这样的，这个output distribution一定要是很集中，因为这是一个非黑即白的世界。假设我们现在做五个class的分类，在class1的几率很大，在其他class的几率很小，这个是好的。在class5的几率很大，在其他class上几率很小，这也是好的。如果今天分布很平均的话，这样是不好的(因为这是一个非黑即白的世界)，这不是符合low-density separation的假设。

但是现在的问题是咋样用数值的方法evaluate这个distribution是好的还是不好的。这边用的是entropy，算一个distribution的entropy，这个distribution entropy告诉你说：这个distribution到底是集中的还是不集中的。我们用一个值来表示distribution是集中的还是分散的，某一个distribution的entropy就是负的它对每一个class的几率乘以log class的几率。所以我们今天把第一个distribution的几率带到这个公式里面去，只有一个是1其他都是0，你得到的entropy会得到是0($E(y^u)=-{\sum }_{m=1}^5{y}_m^u(ln{y}^u)$),第二个也是0。第三个entropy是$ln5$。散的比较开(不集中)entropy比较大，散的比较窄(集中)entropy比较小。

所以我们需要做的事情是，这个model的output在label data上分类整确，但在unlabel data上的entropy越小越好。所以根据这个假设，你就可以去重新设计你的loss function。我们原来的loss function是说：我希望找一个参数，让我现在在label data上model的output跟正确的model output越小越好，你可以cross entropy evaluate它们之间的距离，这个是label data的部分。在unlabel data的部分，你会加上每一笔unlabel data的output distribution的entropy，那你会希望这些unlabel data的entropy 越小越好。那么在这两个中间，你可以乘以一个weight($ln5$)来考虑说：你要偏向unlabel data多一点还是少一点

在train的时候，用GD来一直minimize这件事情，没有什么问题的。unlabel data的角色就很像regularization，所以它被称之为 entropy-based regulariztion。之前我们说regularization是在原来的loss function后面加一个惩罚项(L2,L1)，让它不要overfitting；现在加上根据unlabel data得到的entropy 来让它不要overfitting。

半监督SVM

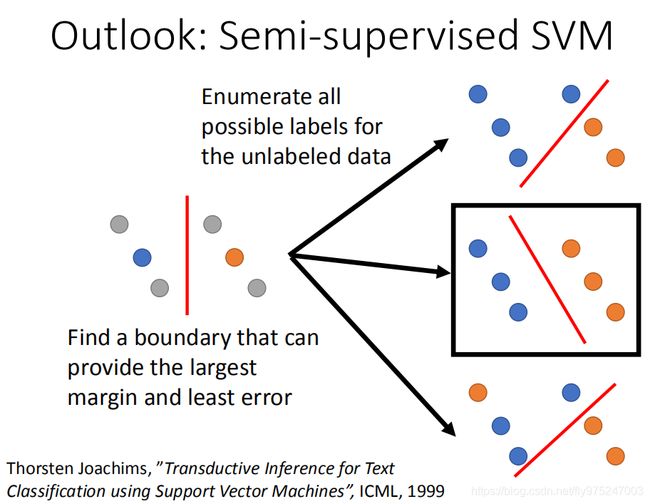
那还有其他semi-supervised的方式，叫做semi-supervised SVM。SVM精神是这样的：SVM做的事情就是：给你两个class的data，找一个boundary，这个boundary一方面要做有最大的margin(最大margin就是让这两个class分的越开越好)同时也要有最小的分类的错误。现在假设有一些unlabel data，semi-supervised SVM会咋样处理这个问题呢？它会穷举所有可能的label，就是这边有4笔unlabel data，每一笔它都可以是属于class1，也可以是属于class2，穷举它所有可能的label(如右图所示)。对每一个可能的结果都去做一个SVM，然后再去说哪一个unlabel data的可能性能够让你的margin最大同时又minimize error。

问题：穷举所有的unlabel data label，这是非常多的事情。这篇paper提出了一个approximate的方法，基本精神是：一开始得到一些label，然后你每次该一笔unlabel data看可不可以让margin变大，变大了就改一下。

假设二：Smoothness Assumption

接下来，我们要讲的方法是Smoothness Assumption。近朱者赤，近墨者黑

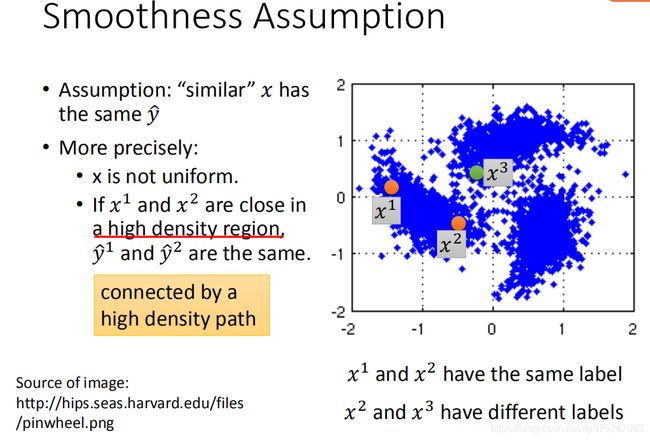
它的假设是这样子的，如果x是相似的，那label y就要相似。光讲这个假设是不精确的，因为正常的model，你给它一个input，如果不是很deep的话，output就很像，这样讲是不够精确的。

真正假设是下面所要说的，x的分布是不平均的，它在某些地方是很集中，某些地方又很分散。如果今天$x_1,x_2$它们在high density region很close的话，$y^1,y^2$才会是是很像的。
high density region这句话就是说：可以用high density path做connection，可以还不知道在说什么。举个例子，假设图中是data的分布，分布就像是写轮眼一样，那现在假设我们有三笔data($x_1,x_2,x_3$)。如果我们今天考虑的是比较粗略的假设(相似的x，那么output就很像，那感觉$x_2,x_3$的label比较像，但$x_1,x_2$的label是比较不像)，其实Smoothness Assumption更精确的假设是这样的，你的相似是要透过一个high density region。比如说，$x_1,x_2$它们中间有一个high density region($x_1,x_2$中间有很多很多的data，他们两个相连的地方是通过high density path相连的)。根据真正Smoothness Assumption的假设，它要告诉我们的意思就是说：$x_1,x_2$是可能会有一样的label，$x_2,x_3$可能会有比较不一样的label(他们中间没有high density path)。

那为什么会有Smoothness Assumption这样的假设呢？因为在真实的情况下是很多可能成立的

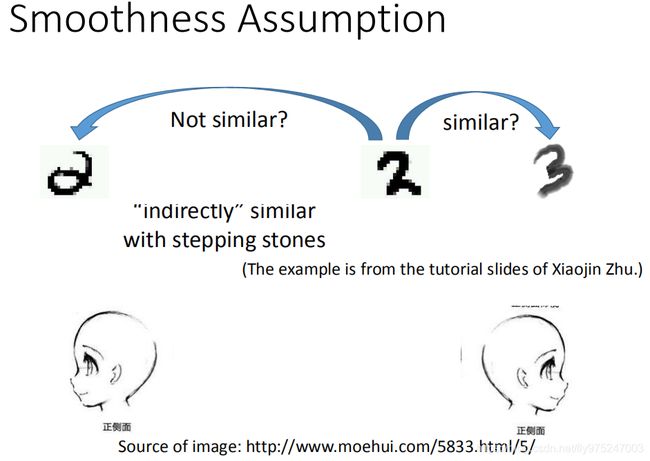
比如说，我们考虑这个例子(手写数字辨识的例子)。看到这变有两个2有一个3，单纯算它们peixel相似度的话，搞不好，两个2是比较不像的，右边两个是比较像的(右边的2和3)。如果你把你的data都通通倒出来的话，你会发现这个2(最左边)跟这个2(右边)中间有很多连续的形态(中间有很多不直接相连的相似，但是有很多stepping stones可以直接跳过去)。所以根据smoothness Assumption的话，左边的2跟右边的2是比较像的，右边的2跟3中间没有过渡的形态，它们两个之间是不像的。如果看人脸辨识的是，也是一样的。如果从一个人的左脸照一张相跟右脸照一张相，这是差很多的。如果你拿另外一个人眼睛朝左的相片来比较的话，会比较像这个跟眼睛朝右相比的话。如果你收集更多unlabel data的话，在这一张脸之间有很多过渡的形态，眼睛朝左的脸跟眼睛朝向右的脸是同一个脸。

[外链图片转存失败(img-n5zvx47s-1569328440254)(res/chapter23-17.png)]
这一招在文件分类上也是非常有用的，这是为什么呢？假设你现在要分天文学跟旅游类的文章，那天文学有一个固定的word distribution，比如会出现“asteroid,bright”.那旅游的文章会出现“yellowstone,zion等等”。那如果今天你的unlabel data跟你的label data是有overlap的话，你就很轻易处理这个问题。但是在真是的情况下，你的unlabel data跟label data中间没有overlap word。为什么呢？一篇文章可能词汇不是很多，但是word多，所以你拿到两篇，有重复的word比例其实是没有那么多的。所以很有可能你的unlabel data跟label data之间是没有任何关系的。

但是如果能收集到够多的unlabeled data的话，就能得到d1和d5比较像，d5和d6比较像，这个像就可以一直传播过去，得到d1和d3像，同样的d4可以和d2一类。

聚类和标记

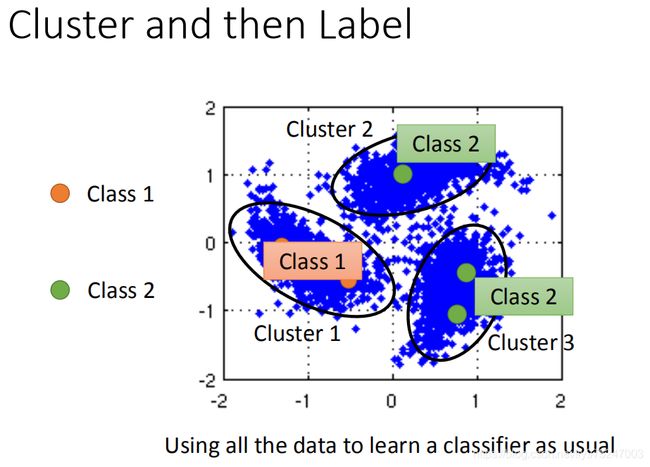
如何实践这个smoothness assumption，最简单的方法是cluster and then label。现在distribution长这么样子，橙色是class1，绿色是class2，蓝色是unlabel data。接下来你就做一下cluster，你可能分成三个cluster，然后你看cluster1里面class1的label data最多，所以cluster1里面所有的data都算是class1，cluster2，cluster3都算是class2、class3，然后把这些data拿去learn就结束了，但是这个方法不一定有用。如果你今天要做cluster label，cluster要很强，因为这一招work的假设就是不同class cluster在一起。可是在image里面，把不同class cluster在一起是没有那么容易的。我们之前讲过说，为什么要用deep learning，不同class可能会长的很像，也有可能长的不像，你单纯只有pixel来做class，你结果是会坏掉的。如果你要让class and then label这个方法有用，你的class要很强。你要用很好的方法来描述image，我们自己试的时候我们会用deep autoendcoder，用这个来提取特征，然后再进行聚类。

基于图的方法

刚才讲的是很直觉的方法，另外一个方法是Graph-based Approach，我们用Graph-based approach来表达这个通过高密度路径连接这件事情。就说我们现在把所有的data points都建成一个graph，每一笔data points都是这个graph上一个点，要想把他们之间的range建出来。有了这个graph以后，你就可以说：high density path的意思就是说，如果今天有两个点，他们在这个graph上面是相的(走的到)，那么他们这就是同一个class，如果没有相连，就算实际的距离也不是很远，那也不是同一个class。

建一个graph：有些时候这个graph representation是很自然就得到了。举例来说：假设你现在要做的是网页的分类，而你有记录网页之间的Hyperlink，那Hyperlink就很自然的告诉你网页之间是如何连接的。假设现在做的是论文的分类，论文和论文之间有引用之间的关系，这个引用也是graph，可以很自然地把图画出来给你。

但有时候你要想办法来建这个graph。通常是这样做的：你要定义$x^i,x^j$咋样来算它们的相似度。影像的话可以用pixel来算相似度，但是performance不太好。用auto-encoder算相似度可能表现就会比较好。算完相似度你就可以建graph，graph有很多种：比如说可以建K Nearest Neighbor，K Nearest Neighbor意思就是说，我现在有一大堆的data，data和data之间，我都可以算出它们的相似度，那我K=3(K Nearest Neighbor)，每一个point跟他最近的三个point做标记。或者也可以做e-Neighborhood:意思就是说，每个点只有跟它相似度超过某一个threshold,跟它相似度大于的1点才会连起来。所谓的edge也不是只有相连不相连这样boundary的选择而已，你可以给edge一些weight，你可以让你的edge跟你的要被连接起来的两个data points的相似度是成正比的。怎么定义这个相似度呢？我会建议比较好的选择就是Gaussian Radial Basis function来定义这个相似度。

怎么算这个function呢？你可以先算说：$x^i,x^j$你都把它们用vector来描述的话，算他们的distance乘以一个参数，再取负号，然后再算exponentiation。其实exponential这件事在经验上还是会给你比较好的performance。为什么用这样的方式会给你比较好的performance呢？如果你现在看这个function(Gaussian Radial Basis function)它的下降速度是非常快的。你用这个Gaussian Radial Basis function的话，你能制造出像这个图(有两个橙色距离很近，绿色这个点离橙色也蛮近，如果你用exponential的话，每一个点只能与非常近的点离,它跟稍微远一点就不连了。你要有这样的机制，你才能避免跨海沟的link，所以你用exponential通常效果比较好。

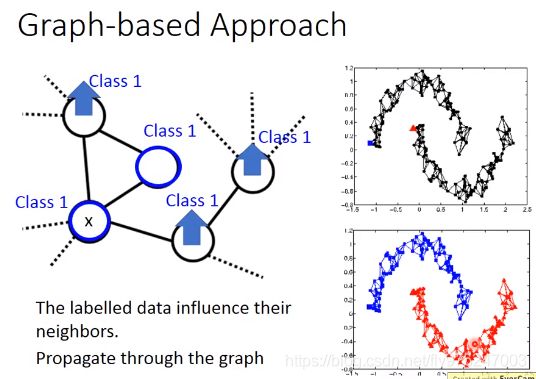
如果我们现在在graph上有一些label data，在这个graph上我们说这笔data1是属于class1，那跟它有相连的data points属于class1的几率也会上升，所以每笔data会影响它的邻居。光是会影响它的邻居是不够的，如果你只考虑光是影响它的邻居的话可能帮助是不会太大。为什么呢？如果说相连的本来就很像，你train一个model，input很像output马上就很像的话，帮助不会太大。那graph-based approach真正帮助的是：它的class是会传递的，本来这个点有跟class1相连所以它会变得比较像class1。但是这件事会像传染病一样传递过去，虽然这个点真正没有跟class1相连，因为像class1这件事情是会感染，所以这件事情会通过graph link传递过来。

举例来说看这个例子，你把你的data points建成graph，这个如果是理想的例子的话，一笔label是属于class1(蓝色)，一笔label是属于class2(红色)。经过garph-based approach，你的graph建的这么漂亮的话(上面都是蓝色的，下面都是红色的)

这样的semi-supervised有用，你的data要足够多，如果data不够多的话，这个地方没收集到data，那这个点就断掉了，那这个information就传不过去了，比如右上图就出现四个小的cluster。

刚才是定性的说使用这个graph，接下来说怎么定量使用这个graph。那这个定量的使用是在这个graph structure上面定义一个东西叫做：label的 smoothness，我们会定义说label有多符合我们刚才说的smoothness assumption 的假设。

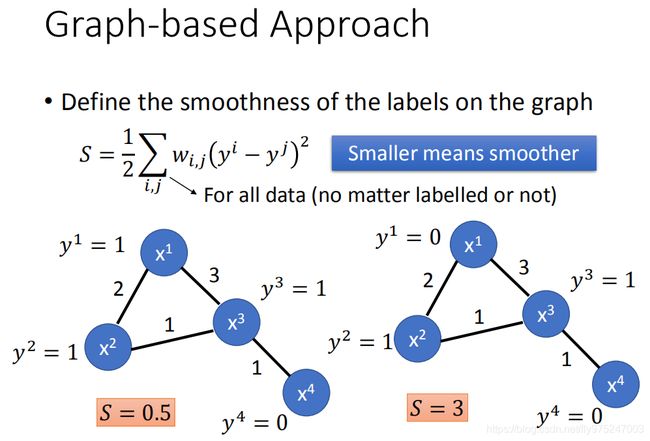
现在看这两个例子，在这两个例子都有四个data points，data point跟data point连接的数字代表了weight。在左边这个例子中，你给它的label是(1,1,1，0)，在右边的例子中，给的label是(0,1,1,0)。左边的这个例子是比较smothness的，但是我们需要一个数字定量的描述它说：它有多smothness。常见的做法是这样子的：这个式子是我们考虑两两有相连的point，两两拿出来(summation over所有data i,j)，然后计算i,j之间的weight跟y的label减去j的label的平方(这个是summation 所有data，不管他现在是有label还是没有label)。所以你看左边这个case，在summation over所有的data的时候，你只需要考虑,s=0.5(只是在计算时比较方便而已，没有真正的效用)，右边的class s=3，这个值(s)越小越smothness，你会希望你得出的labelsmothness的定义算出来越小越好。

现在看这两个例子，在这两个例子都有四个data points，data point跟data point连接的数字代表了weight。在左边这个例子中，你给它的label是(1,1,1，0)，在右边的例子中，给的label是(0,1,1,0)。左边的这个例子是比较smothness的，但是我们需要一个数字定量的描述它说：它有多smothness。常见的做法是这样子的：$S=\frac{1}{2}{\sum }_{ij}{w}_{i,j}(y^i-y^j{)}^2$。这个式子是我们考虑两两有相连的point，两两拿出来(summation over所有data i,j)，然后计算i,j之间的weight跟y的label减去j的label的平方(这个是summation 所有data，不管他现在是有label还是没有label)。所以你看左边这个case，在summation over所有的data的时候，你只需要考虑$x_3,x_4$,s=0.5(只是在计算时比较方便而已，没有真正的效用)，右边的class s=3，这个值(s)越小越smothness，你会希望你得出的labelsmothness的定义算出来越小越好。

这个算式可以稍微整理整理一下，可以写成一个简洁的式子。我们把y串成一个vector(现在y包括label data，也包括unlabel data)，每一个笔label data和label data都赋一个值给你，现在你有R+U个dimension vector，可以写成y。如果你这样写的话，s这个式子可以写成y(vector)的transform乘以L(matrix)再乘以y，L是属于(R+U)*(R+U)matrix，这个L被叫做“Graph Laplacian”。

这个L的定义是：两个matrix相减(L=D-W)。W就是你把这些data point两两之间weight connection建成一个matrix，这个matrix的四个row个四个columns分别代表data$x^1$到$x^4$,D是你把w的每组row合起来。

现在我们可以用$y^{T}Ly$去评估我们现在得到的label有多smothness。在这个式子里面我们会看到有y，这个y是label，这个label的值也就是neural network output的值是取决于neural parameters。这一项其实是neural 的depending，所以你要把graph的information考虑到neural network的train的时候，你要做的事情其实就是在原来的loss function里面加一项。假设你原来的loss function是cross entropy，你就加另外一项，你加的这一项是smoothness的值乘以某一个你想要调的参数，后面这一项$\lambda$S其实就是象征了 regulization term。你不只要调整参数让你那些label data的output跟真正的label越接近越好，你同时还要做到说：output这些label，不管是在label data还是在unlabel data上面，它都符合smothness assuption的假设是由这个s所衡量出来的。所以你要minimize前一项还要minimize后一项(用梯度下降)

其实你要算smothness时不一定要放在output的地方，如果你今天是deep neural network的话，你可以把你的smothness放在network任何地方。你可以假设你的output是smooth，你也可以同时说：我把某一个hidden layer接出来再乘上别的一些transform，它也要是smooth，也可以说每一个hidden layer的output都是smooth

Better Representation

最后一个方法是：Better Representation，这个方法的精神是：“去无存青，化繁为简”，等到unsupervised的时候再讲。
它的精神是这样子的：我们观察到的世界其实是很复杂的，我们在我们观察到的世界背后其实是有一些比较简单的东西在操控着我们这个复杂的世界，所以你只要能看透这个世界的假象，直指它的核心的话就可以让训练变得容易。