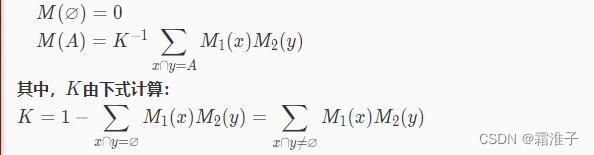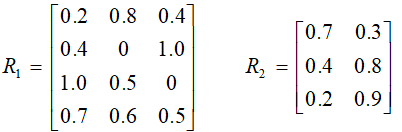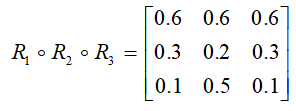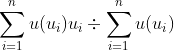【五】头歌平台实验-不确定性推理
在现实世界中的事物以及事物之间的关系是极其复杂的。由于客观上存在的随机性、模糊性以及某些事物或现象暴露得不充分性,导致人们对它们的认识往往是不精确、不完全的,具有一定程度的不确定性。这种认识上的的不确定性反映到知识以及由观察所得到的证据上来,就分别形成了不确定性的知识及不确定性的证据。人们通常是在信息不完善、不精确的情况下运用不确定性知识进行思维、求解问题的,推出的结论也是不确定的。因而还必须对不确定性知识的表示及推理进行研究。
第1关:可信度方法
1、如果证据 E 的出现使得结论 H 一定程度为真,则可信度因子(C)
A、-1< CF( H , E ) <0
B、CF( H , E ) = 1
C、0 < CF( H , E ) < 1
D、CF( H , E ) = 0
2、在可信度方法中,若证据 A 的可信度 CF(F)=0,这意味着(A )
A、对证据 A 一无所知
B、证据 A 可信
C、没有意义
D、证据 A 不可信
3、设有如下一组推理规则: r1: IF E1 THEN E2 (0.6) r2: IF E2 AND E3 THEN E4 (0.8) r3: IF E4 THEN H (0.7) r4: IF E5 THEN H (0.9) 且已知CF(E1)=0.5,CF(E3)=0.6,CF(E5)=0.4,结论H的初始可信度一无所知,则CF(H)=( D)
A、0.168
B、0.24
C、0.36
D、0.47
相关知识:
1、不确定性推理概述
不确定性推理就是从不确定性的初始证据出发,通过运用不确定的知识,最终推出具有一定程度的不确定性但确实合理或者近乎合理的结论和思维过程。
在不确定性推理中,知识和证据都具有某种程度的不确定性,这就为推理机的设计与实现增加了复杂性和难度。它除了必须解决推理方向、推理方法、控制策略等基本问题外,一般还需要解决不确定性的表示与度量、不确定性匹配、不确定性的传递算法以及不确定性的合成等重要问题。常用的不确定性推理方法有可信度方法、主观 Bayes 方法、证据理论。
2、可信度方法
可信度方法是在确定性推理的基础上,结合概率论等提出一种不确定性推理方法。简单的来说就是,我们在平时生活中积累了大量的经验,当我们面临一个新事物或新情况时,我们可以根据以前的经验对问题的真、假做出判断。这种根据经验对一个事物或现象为真的相信程度称为可信度。显然,这种方法带有很大的主观性和经验性,其准确性很难把握。但是由于人工智能面对的往往是结构不良的问题,难以给出精确的模型,先验概率及条件概率的确定又比较困难。所以用可信度方法来表示知识和证据的不确定性不失为一种可行的方法。
3、C-F 模型
C-F 模型是基于不确定性推理的基本方法,其他可信度方法都是在此基础上发展起来的。根据不确定性推理简介,我们需从以下几个方面来进行分析。
- 知识不确定性的表示
在 C-F 模型中,知识是用产生式规则表示的,其一般形式为: IF E THEN H (CF(H,E))
其中,E是知识的前提条件;H是知识的结论,CF(H,E)是知识的可信度。CF(H,E)的取值范围为[−1,1],若由于相应的证据出现,增加结论H为真的可信度,则取CF(H,E)>0,证据的出现越是支持H为真,就使CF(H,E)的值越大;反之,取CF(H,E)<0,证据的出现越是支持H为假,就使CF(H,E)的值越小;若证据的出现与H无关,则取CF(H,E)=0。
例如:IF 发烧 AND 流鼻涕 THEN 感冒 (0.8)
表示当某人确实有“发烧”及“流鼻涕”症状时,则有80%的把握是患了感冒。
- 证据不确定性的表示
在 C−F 模型中,证据的不确定性也是可用可信度因子表示的。
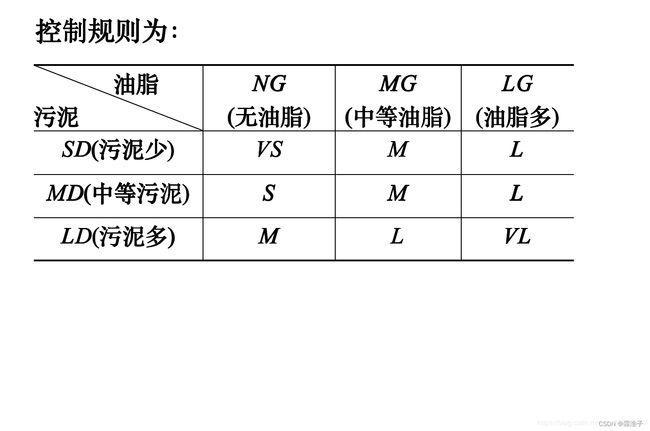
例如,CF(E)=0.6表示E的可信度度为 0.6。 同样的,CF(E)的取值范围也为[−1,1]。对于初始证据,若对它的所有观察S,能肯定它为真,则CF(E)=1;若肯定它为假,则CF(E)=−1;若它以某种程度为真,则0 C-F 模型中的不确定性推理从不确定性的初始证据出发,通过运用不相关的不确定性知识,最终推出结论,并求出结论的可信度值。其中结论H的可信度由下式计算: CF(H)=CF(H,E)×max{0,CF(E)} 若由多条不同知识推出相同的结论,但可信度不同,则可以用合成算法求出综合可信度。 由于对多条知识的综合,可以通过两两的合成实现,所以下面只考虑两条知识的情况。 设有如下知识: IF E1 THEN H (CF(H,E1)) IF E2 THEN H (CF(H,E2)) 则结论H的综合可信度可分为如下两步算出: 1.分别对每一条知识求出CF(H) CF(H)=CF(H,E1)×max0,CF(E1) CF(H)=CF(H,E2)×max0,CF(E2) 2.用下述公式求出E1与E2对H所形成的可信度CF12(H) 1、在证据理论中,信任函数与似然函数对(Bel(A),Pl(A))的值为(0,0)时,表示(D ) A、对 A 一无所知 B、A 为真 C、对 A 为真有一定信任 D、A 为假 2、基本概率分配函数之值是概率。 A、对 B、错 3、设样本空间D=a,b,c,d,M1、M2为定义在2D上的概率分配函数: M1:M1(b,c,d)=0.7,M1(a,b,c,d)=0.3,M1的其余基本函数均为0 M2:M2(a,b)=0.6,M2(a,b,c,d)=0.4,M2的其余基本函数均为0 则,它们的正交和M=M1⊕M2=(A ) A、0 B、0.28 C、0.42 D、0.18 证据理论由德普赛斯于 20 世纪 60 年代提出,并由沙佛在 20 世纪 70 年代中期进一步发展起来的一种不确定性的理论,所以,又称为 D-S 理论。该理论能够区分“不确定”与“不知道”的差异,具有较大的灵活性,因而受到人们重视。目前,在证据的基础上已经发展了多种不确定性模型。证据理论是用集合表示命题的。设D是变量x所有取值的集合,且D中的元素是互斥的,在任一时刻x都只能取D中的某一元素为值,则称D为x的样本空间。在证据理论中,D中任何一个子集A都对应于一个关于x的命题,则称该命题“x的值在A中”。 例如x代表打靶时所击中的环数,D=1,2,...,10,则A=5表示“x的值是5”或者“击中的环数是5”,A=5,6,7,8表示“击中的环数是5,6,7,8”中的某一个。 证据理论中,为了描述和处理不确定性,引入了概率分配函数、信任函数以及似然函数,接下来我们来介绍一下这三个函数。 定义1:设函数M:2D→[0,1],即对任何一个属于D的子集A,命它对应一个数M∈[0,1],且满足: 则称M是2D上的基本概率分配函数,M(A)称为A的基本概率函数。 关于概率分配函数,有几点需要注意: 1.假设样本空间D有n个元素,则D中子集的个数为2的n次个,定义中的2的D次就是表示这些子集的。比如D=红,黄,蓝,则它的子集正好是2的3次=8个。具体为 A1=红,A2=黄,A3=蓝,A4=红,黄, A5=红,蓝,A6=黄,蓝,A7=红,黄,蓝,A8=∅ 2.概率分配函数的作用是把D的任意一个子集A都映射为[0,1]上的一个数M(A)。概率分配函数实际上是对D的各个子集进行信任分配,M(A)表示分配给A的那一部分。例如,设A=红,M(A)=0.3,表示对命题"x是红色"的正确性的信任度是 0.3。注意当A是由多个元素组成时,M(A)不包括对A的子集的信任度,也不知道它如何进行分配。例如,在M(红,黄)=0.2不包括A=红的信任度为0.3,而且也不知道该把这个0.2分配给{红}还是{黄}。 3.概率分配函数与概率不同,例如,设D=红,黄,蓝且设 M(红)=0.3,M(黄)=0,M(蓝)=0.1, M(红,黄)=0.2,M(红,蓝)=0.3,M(黄,蓝)=0, M(红,黄,蓝)=0.1,M(∅)=0 显然,M符合概率分配函数的定义,但是 M(红)+M(黄)+M(蓝)=0.4 若按概率的要求,这三者的和应等于1。 定义2:命题的信任函数Bel: Bel函数又称为下限函数,Bel(A)表示对命题A为真的总的信任程度。由信任函数及概率分配函数的定义容易推出: Bel(∅)=M(∅)=0, 根据上面给出的数据,可以求得 Bel(红)=M(∅)=0 Bel(红,黄)=M(红)+M(黄)+M(红,黄)=0.3+0.2=0.5 Bel(红,黄,蓝)=M(红)+M(黄)+M(蓝)+M(红,黄)+M(红,蓝)+M(黄,蓝)+M(红,黄,蓝)=0.3+0+0.1+0.2+0.2+0.1+0.1=1 定义3:似然函数Pl: 由于Bel(A)表示对A为真的信任程度,所以Bel(¬A)就表示对¬A为真,即A为假的信任程度,由此可推出Pl(A)表示对A为非假的信任程度。 下面来看两个例子,其中用到的基本函数仍为上面给出的数据。 Pl(红)=1−Bel(¬红) =1−Bel(黄,蓝) =1−[M(黄)+M(蓝)+M(黄,蓝)] =1−[0+0.1+0.1] =0.8 Pl(黄,蓝)=1−Bel(¬黄,蓝) =1−Bel(红) =1−0.3 =0.7 有时对同样的证据会得到两个不同的概率分配函数,例如,对样本空间D=a,b从不同的来源分别得到如下两个分配概率函数: M1(a)=0.3,M1(b)=0.6,M1(a,b)=0.1,M1(∅)=0 M2(a)=0.4,M2(b)=0.4,M2(a,b)=0.2,M2(∅)=0 定义4:设M1和M2是两个概率分配函数,则其正交和M=M1⊕M2为 如果K 前面我们已经详细地介绍了证据理论的各种函数,接下来,我们来熟悉一下基于证据理论的不确定性推理。基于证据的不确定性推理,大体可分为以下步骤: 1.建立问题的样本空间D; 2.由经验给出,或者由随机性规则和事实的信度度量计算,求得幂集2D的基本概率分配函数; 3.计算所关心的子集A∈2D的信任函数值Bel(A)或者似然函数值Pl(A); 4.由Bel(A)或者Pl(A)得出结论。 范例: (1)如果 流鼻涕 则 感冒但非过敏性鼻炎(0.9) 或 过敏性鼻炎但非感冒(0.1) (2)如果 眼发炎 则 感冒但非过敏性鼻炎(0.8) 或 过敏性鼻炎但非感冒(0.05) 又有事实: (1)小王流鼻涕(0.9) (2)小王眼发炎(0.4) 括号中的数字表示规则和事实的可信度,我们的目标是要知道小王患的什么病? 综合上述结果得: “感冒但非过敏性鼻炎”为真的信任度为0.87,非假的信任度为0.934; “过敏性鼻炎但非感冒”为真的信任度为0.066,非假的信任度为0.13。 因此,患者是感冒了而非过敏性鼻炎。 1、设有论域U=x1,x2,x3,x4,x5,A、B是U上的两个模糊集,且有 A=0.85/x1+0.7/x2+0.9/x3+0.9/x4+0.7/x5 B=0.5/x1+0.65/x2+0.8/x3+0.98/x4+0.77/x5 则A∩B=(A) A、0.5/x1+0.65/x2+0.8/x3+0.9/x4+0.7/x5 B、0.85/x1+0.7/x2+0.9/x3+0.98/x4+0.77/x5 C、0.15/x1+0.3/x2+0.1/x3+0.1/x4+0.3/x5 D、0.5/x1+0.3/x2+0.8/x3+0.1/x4+0.3/x5 2、设有论域U=x1,x2,x3,x4,x5,A、B是U上的两个模糊集,且有 A=0.85/x1+0.7/x2+0.9/x3+0.9/x4+0.7/x5 B=0.5/x1+0.65/x2+0.8/x3+0.98/x4+0.77/x5 则A∪B= A、0.5/x1+0.65/x2+0.8/x3+0.9/x4+0.7/x5 B、0.85/x1+0.7/x2+0.9/x3+0.98/x4+0.77/x5 C、0.15/x1+0.3/x2+0.1/x3+0.1/x4+0.3/x5 D、0.5/x1+0.3/x2+0.9/x3+0.9/x4+0.3/x5 3、设有论域U=x1,x2,x3,x4,x5,A、B是U上的两个模糊集,且有 A=0.85/x1+0.7/x2+0.9/x3+0.9/x4+0.7/x5 B=0.5/x1+0.65/x2+0.8/x3+0.98/x4+0.77/x5 则¬A= A、0.5/x1+0.65/x2+0.8/x3+0.9/x4+0.7/x5 B、0.85/x1+0.7/x2+0.9/x3+0.98/x4+0.77/x5 C、0.15/x1+0.3/x2+0.1/x3+0.1/x4+0.3/x5 D、0.85/x1+0.7/x2+0.9/x3+0.9/x4+0.7/x5 4、设有如下两个模糊关系: 则: A、对 B、错 5、设有如下两个模糊关系: 则: A、错 B、对 “模糊”是人类感知万物,获取知识,思维推理,决策实施的重要特征。 “模糊”比“清晰”所拥有的信息容量更大,内涵更丰富,更符合客观世界。为了用数学方法描述和处理自然界出现的不精确、不完整的信息,如人类语言信息和图像信息,1965 年美国著名学者加利福尼亚大学教授扎德发表了关于“ fuzzy set ”的论文,首次提出了模糊理论。 在人工智能领域,特别是在知识表示方面,模糊逻辑有相当广阔的应用背景。目前在自动控制、模式识别、自然语言理解、机器人及专家系统等研制方面,应用模糊逻辑取得了一定的成就,引起了本领域越来越多专家的关注。 模糊集合是经典集合的补充。下面首先介绍集合论中的几个名词。 对比以下经典集合,论域就相当于值域,元素概念与集合的概念两者是相等的。但是在经典集合中,元素a与集合A的关系只有两种关系:a属于A或a不属于A,即只有两个真值“真”和“假”。它只能描述确定性的概念,而不能描述现实世界中模糊的概念。例如,“天气很热”等概念。 模糊推理模仿人类的智慧,引入隶属度的概念,描述介于“真”与“假”中间的过程。 模糊集合中每一个元素被赋予一个介于 0 和 1 之间的实数,描述其元素属于这个模糊集合的强度,该实数称为元素属于这个模糊集合的隶属函数。 模糊集合是经典集合的推广,实际上,经典集合是模糊集合中隶属函数取0或1时的特例。知道了模糊集合的概念,接下来的问题就是怎么去表示它,与经典集合表示不同的是,模糊集合中不仅要列出属于这个集合的元素,而且要注明这个元素属于这个集合的隶属度。当论域中元素数目有限时,模糊集合A的数学描述为A=(x,μA(x)),x∈X。其中μA(x)为元素x属于模糊集A的隶属度,X是元素x的论域。 几种不同的表示法: 在模糊集合中,模糊关系也占有很重要的地位。模糊关系是普通关系的推广。普通关系是描述两个集合中元素之间是否有关联。模糊关系描述两个模糊集合中元素之间关联程度。当论域有限时,可以采用模糊矩阵表示模糊关系。 说到推理,我们首先想到的就是知识表示,在进行模糊推理时,首先要进行的就是模糊知识表示。在前面的实训中,我们提到由于模糊不确定性,一般采用隶属度来刻画。隶属度是一个命题中所描述的事物的属性、状态和关系等的强度。例如我们用三元组(张三,体型,(胖,0.9))表示命题“张三比较胖”,其中的 0.9 就代替“比较”而刻画了张三“胖”的程度。这种隶属度表示法,一般是一种针对对象的表示法。模糊知识表示一般形式为(<对象>,<属性>,(<属性值>,<隶属度>))。 事实上,这种思想和方法还可广泛用于产生式规则、逻辑规则、谓词逻辑、框架、语义网络等多种表示方法,从而扩充它们的表示范围和能力。一般,人类思维判断的基本形式是 如果 (条件) → 则 (结论) 其中的条件和结论常常是模糊的。 例如,对下列模糊知识 如果 压力较高且温度在缓慢上升 则 阀门略开 其中的条件和结论常常是模糊的。 许多模糊规则实际上是一组多重条件语句,可以表示为从条件论域到结论论域的模糊关系矩阵R。通过条件模糊向量与模糊关系 R 的合成进行模糊推理,得到结论的模糊向量,然后采用清晰化的方法将模糊结论转化精确量。 对于 IF A THEN B 类型的模糊规则的推理,若已知A,则输出为B;若现在已知输出为A′,则输出B′。用合成规则求取 由上述模糊推理得到的结论或者操作是一个模糊向量,不能直接应用,需要先转化为确定值。将模糊推理得到的模糊向量,转化为确定量的过程为“模糊决策”,或者“模糊判决”,“清晰化”,“反模糊化”等。下面介绍几种简单、实用的模糊决策的方法。 1.最大隶属度法 最大隶属度法是在模糊向量中,取隶属度最大的量作为推理结果。例如,当得到的模糊向量为: U’=0.1/2+0.4/3+0.7/4+1.0/5+0.7/6+0.3/7 由于推理结果隶属于等级5的隶属度为最大,所以取结论为U=5,如果有两个以上的元素均为最大(一般依次相邻),则可以取它们的平均值。例如: U’=0.5/−3+0.5/−2+0.5/−1+0.0/0+0.0/1+0.0/2+0.0/3 则U=3−3−2−1=−2。这种方法的优点就是简单易行,缺点是完全排除了其他隶属度较小的量的影响和作用,没有充分利用推理过程取得的信息。 2.加权平均判决法 为了克服最大隶属度法的缺点,可以采用加权平均判决法,即U= 例如:U’=0.1/2+0.6/3+0.5/4+0.4/5+0.2/6 则U=(2*1+3*0.6+4*0.5+5*0.4+6*0.2)/(0.1+0.6+0.5+0.4+0.2)=4 3.中位数法 论域上把隶属函数曲线与横坐标围成的面积,分为两部分的元素称为模糊集的中位数。中位数法就是把模糊集的中位数作为系统控制量。 与最大隶属度法相比,这种方法利用了更多的信息,但计算比较复杂,特别是在连续隶属度函数时,需要求解积分方程,因此应用场合要比加权平均法小。加权平均法比中位数法具有更佳的性能,而中位数法的模糊控制器类似于多级继电器控制,加权平均法则类似于 PI 控制器。一般情况下,都优于最大隶属法。 至此,我们已经学习完了关于模糊推理的全部理论,接下来我们将这套理论应用到设计模糊逻辑推理系统中。要设计模糊逻辑推理系统,需要知道以下基本步骤: 1.确定输入/输出的模糊子集及其论域; 2.选择控制规则; 3.规则的关系运算(蕴含,合成); 4.精确化过程。 范例: 选择了一个模糊洗衣机控制系统的模拟。 1.确定输入/输出的模糊子集以及论域 该系统中,设计了一个衣服上的油污、污渍的参数, 污泥{ SD (污泥少), MD (中等污泥), LD (污泥多)} 油脂{ NG (无油脂), MG (中等油脂), LG (油脂多)} 控制对象是洗衣机的洗涤时间,论域:[0,60] 输入是被洗衣物的污泥和油脂,论域:[0,100] 输出的是洗衣机的洗涤时间: 洗涤时间{ VS (很短), S (短), M (中等), L (长), VL (很长)} 2.选择控制规则 3.规则的关系运算(蕴含,合成) 污泥、污渍以及洗涤时间的隶属度函数的解析表达式如下: 4.精确化过程 通过最大隶属度函数,来计算模糊控制输出的量化值。 -END-
第2关:证据理论
相关知识:
1、证据理论
2、概率分配函数
3、信任函数
![]() →[0,1],且
→[0,1],且4、似然函数
![]() →[0,1],且 Pl(A)=1−Bel(¬A) ,∀A⊆D
→[0,1],且 Pl(A)=1−Bel(¬A) ,∀A⊆D5、概率分配函数的正交和
![]()
![]() 0,则正交和M也是一个概率分配函数;如果K=0,则不存在正交和,也不可能存在概率函数,称M1与M2矛盾。 对于多个概率分配函数M1,M2,...,Mn,如果它们可以组合,也可通过正交和运算将它们组合为一个概率分配函数。
0,则正交和M也是一个概率分配函数;如果K=0,则不存在正交和,也不可能存在概率函数,称M1与M2矛盾。 对于多个概率分配函数M1,M2,...,Mn,如果它们可以组合,也可通过正交和运算将它们组合为一个概率分配函数。6、基于证据理论的不确定性推理
第3关:模糊推理基础
相关知识:
1、模糊逻辑的提出
2、模糊集合
3、模糊关系
第4关:模糊推理及其应用
def ruleMD(stain):
if stain < 0 or stain > 100:
return 0.0
else: # 当传入的参数在0-100之间时,该处有两种情况
# 计算MD的结果,并且和同参数下的SD结果相比较,得出一个结果
if stain >= 0 and stain <= 50:
return stain / 50.0
else:
# 同上的操作,得出结果和同参数下的LD相比较
return (100 - stain) / 50.0
def ruleSD(stain):
# SD部分的rule
# 当输入的参数0 <= x <= 50, 执行该方法
result = (50 - stain) / 50.0
returnMDresult = ruleMD(stain)
# 传参数到MD中,计算,并比较
# 1、相同,则返回结果为SD,2、SD的结果大,则返回SD,3、MD的结果大,则返回MD的返回值
if result < returnMDresult:
return 2.0
else:
return 1.0
def ruleLD(stain):
# LD部分的rule
# 当输入的参数在50 - 100之间时,执行
result = (stain - 50) / 50
returnMDresult = ruleMD(stain)
# 同时将参数传入给MD,同时比较MD方法传回来的参数和该方法求出的值相比较,求出最后的最适合的预测值
# ********** Begin **********#
if result < returnMDresult:
return 2.0
else:
return 3.0
# ********** End **********#
def ruleMG(oil):
# 当传入的参数在0 - 100之间时,该处有两种情况
if oil < 0 or oil > 100:
return 0 # 当在论域之外时,直接返回无结果
else:
if oil >= 0 and oil <= 50:
return oil / 50.0 # 计算MD的结果,并且和同参数下的SD结果相比较,得出一个结果
else:
return (100 - oil) / 50 # 同上的操作,得出结果和同参数下的LD相比较
def ruleSG(oil):
if oil < 0 or oil > 50:
return 0.0
else:
# SG部分的rule
# 当输入的参数0<=x<=50,执行该方法
result = (50 - oil) / 50.0
returnMGresult = ruleMG(oil)
# 传参数到MD中,计算,并比较
# 1、相同,则返回结果为SD,2、SD的结果大,则返回SD,3、MD的结果大,则返回MD的返回值
if result < returnMGresult:
return 2.0
else:
return 1.0
def ruleLG(oil):
# LD部分的rula
# 当输入的参数在50 - 100之间时,执行
# 同时将参数传入给MG,同时比较MG方法传回来的参数和该方法求出的值相比较,求出最后的最适合的预测值
returnMGresult = ruleMG(oil)
result = (oil - 50) / 50.0
# 比较后,得到预测值
if result < returnMGresult:
return 2.0
else:
return 3.0
# F函数,总的函数,从该函数中分流到rule的三个函数中
def Function(oil, stain):
# VS: SD, SG
# S: MD, SG
# M: SD, MG MD, MG LD, SG
# L: SD, LG MD,LG LD,MG
# XL: LD, LG
# 根据规则输出最后的洗涤时间
# 需要客户的正确输入
# ********** Begin **********#
if stain >= 0 and stain <= 50:
result_D = ruleSD(stain)
else:
result_D = ruleLD(stain)
if oil >= 0 and oil <= 50:
result_G = ruleSG(oil)
else:
result_G = ruleLG(oil)
# ********** End **********#
# 比较最后的结果,返回结果控制规则表,例如VS在表格中的坐标是(1,1),S的坐标是(2,1)
if result_D == 1.0 and result_G == 1.0:
return 1 # return VS
elif result_G == 1.0 and result_D == 2.0:
return 2 # return S
elif (result_D == 1.0 and result_G == 2.0) or (result_G == 2.0 and result_D == 2.0) or (
result_G == 1.0 and result_D == 3.0):
return 3 # reutrn M
elif (result_D == 1.0 and result_G == 3.0) or (result_D == 2.0 and result_G == 3.0) or (
result_D == 3.0 and result_G == 2.0):
return 4 # return L
elif result_G == 3.0 and result_D == 3.0:
return 5 # return VL
相关知识:
1、模糊推理
B′=A′∘R,其中R为A到B的模糊关系。2、模糊决策
3、模糊推理的应用
![]()