【论文笔记】激光里程计 DeepLO:Geometry-Aware Deep LiDAR Odometry 2019

视频链接:链接

使用surfel based 的表示方法（vertex+normal）作为网络的输入，避免了量化损失，看起来是一种不错的表示方法，既没有误差，保留了点云数据的精确性，还以一种map 的形式提供邻域查询功能，不需要KDtree检索之类。

此外，使用几何一致性约束的损失函数进行无监督训练，通过扰动成像的方法证明了损失函数的可行性。并在部分场景上取得了优于有监督训练的精度。

DeePLO同样对点云的表达形式做出了优化,使用了与range image类似的一种图像坐标参数化表示：

$$\left(\begin{array}{l}u\\ v\end{array}\right)=\left(\begin{array}{c}\left(f_h/2-\arctan \left(p^y,p^x\right)\right)/{\delta }_h\\ \left(f_{vu}-\arctan \left(p^z,d\right)\right)/{\delta }_v\end{array}\right)$$
其中（u，v）为投影后的图像坐标，$\mathbf{p}=\left(p^x,p^y,p^z\right)$为3D点云坐标。深度$d={\left(p^{x2}+p^{y2}\right)}^{1/2}$,f_h和f_v分别为水平竖直的视野。如果有多个3D点投影到相同的像素坐标上，则选择最近的点作为像素值。每个像素点（vertex）包括三维的向量$\mathbf{v}=\left[v^x,v^y,v^z\right]$（论文没说是从哪里计算的值，应该是点云的三维坐标）

得到的2D投影图像被称为vertex map V。

同样作为输入的还有点云的normal map N。
即为每一个vertex分配一个法向量。分配方法使用的《NICP: Dense normal based pointcloud registration》的方法法向量计算方法根据V上的最近邻vertex计算。

最后在时刻t 的点云被表示为F={V，N}
效果图:

将vertex map与常用的range image进行对比：

range image的投影公式：
$$\begin{array}{l}\alpha =\arctan (y/x)/\Delta \alpha \\ \beta =\arcsin \left(z/\sqrt{x^2+y^2+z^2}\right)/\Delta \beta \end{array}$$
LO-Net、DMLO均使用了range image
vertex image的投影公式：
$$\left(\begin{array}{l}u\\ v\end{array}\right)=\left(\begin{array}{c}\left(f_h/2-\arctan \left(p^y,p^x\right)\right)/{\delta }_h\\ \left(f_{vu}-\arctan \left(p^z,d\right)\right)/{\delta }_v\end{array}\right)$$
除了本文，还有rangenet++也使用了vertex map

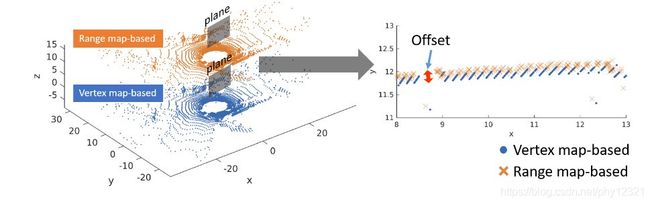
如图，左边是一个点云的两种表示，将其中一个部位（墙的俯视视角）放大至右图可见，range image由于角度离散化而产生了量化误差。而vertex map使用raw point作为表示，因此没有离散化带来的误差。

网络结构：

VertexNet 和 NormalNet分别提取输入前后帧两幅点云的平移特征和旋转特征，然后输入到posenet中进行回归，输出四元数

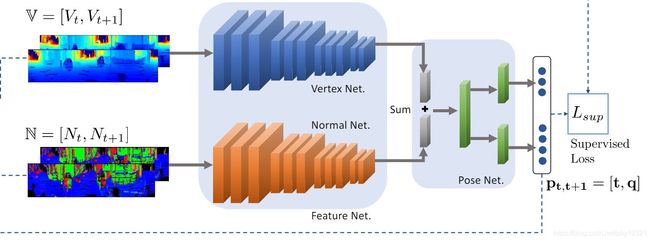
VertexNet 和 NormalNet均使用残差块和全连接网络

DeepLO还针对训练数据的真值提出了有监督和无监督两种训练模式：

无监督损失

• 重投影
  根据网络对t,t+1时刻的相对运动的预测值将t+1时刻的vertex（点云） v_t+1 转换到t时刻得到v_t’,然后将其投影到vertex map，与t时刻的vertex map 对比得到前后帧的vertex和normal vectors的对应关系:

$$\begin{gathered} {\mathbf{v}}_t^{\prime }=T_{t,t+1}{\mathbf{v}}_{t+1} \\ \begin{array}{l}{\overline{\mathbf{v}}}_t=V\left(\pi \left({\mathbf{v}}_t^{\prime }\right)\right)\\ {\overline{\mathbf{n}}}_t=N\left(\pi \left({\mathbf{v}}_t^{\prime }\right)\right)\end{array} \end{gathered}$$

2. 有了对应点的关系，ICP损失:
   $${\mathcal{L}}_{icp}=\sum _{\mathbf{v}\in V_{t+1}}{\overline{\mathbf{n}}}_t\cdot \left(T_{t,t+1}{\mathbf{v}}_{t+1}-{\overline{\mathbf{v}}}_t\right)$$
   代表了对应点之间的法向量距离之和（没有求平均）

3. 但是，如果仅仅使用该损失网络会倾向于输出视场以外的刚性变换，导致没有对应点关系，以此达到最小损失。因此作者引入了filed of view损失函数作为约束：
   $${\mathcal{L}}_{fov}=\sum _{\mathbf{v}\in V_{t+1}}\mathbb{I}\left(\pi \left(T_{t,t+1}\mathbf{v}\right)-(w,h)\right)+\mathbb{I}\left(-\pi \left(T_{t,t+1}\right)\right)$$
   该损失使得预测的旋转量始终将vertex投影在（w，h）的范围内。

总的损失：
$${\mathcal{L}}_{uns}={\mathcal{L}}_{icp}\exp \left(-s_{icp}\right)+s_{icp}+{\mathcal{L}}_{fov}\exp \left(-s_{fov}\right)+s_{fov}$$
作者对该非监督的损失函数进行了评估，在加入平移量和旋转量的扰动后，观察损失函数值：

可以看出损失函数在最优值附近是凸的，这说明使用无监督损失函数进行训练是可行的。

有监督损失

作者使用于勒角$\mathbf{r}=\left[r^x,r^z,r^y\right]$，实验发现比四元数效果更好。

损失函数：
$${\mathcal{L}}_{\text{sup}}={\mathcal{L}}_t\exp \left(-s_t\right)+s_t+{\mathcal{L}}_r\exp \left(-s_r\right)+s_r$$
其中：${\mathcal{L}}_t=\Vert \mathbf{t}-\hat{\mathbf{t}}{\Vert }_l$，${\mathcal{L}}_r=\Vert \mathbf{r}-\hat{\mathbf{r}}{\Vert }_l$,L = 1

实验结果