Pytorch与深度学习 —— 6. 使用 RNNCell 做文字序列的转化之 RNN 入门篇

上一章节里介绍了什么是循环神经网络后，在这一章里，我们来学习如何用RNN网络做一个简单的应用，比如我们把一个文本序列 “apple” 转化为另一个文本 “oppla”，这一章的练习非常重要，因为很多文本分类任务会用到这篇文章里提到知识点。

提出一个好问题

我们先来制定这样一个规则，英语当中有 a, i, u, e, o，然后我们让它随机调换一个顺序，比如 e, i, a, o, u，接下来假设有左边这样一组输入数据，并且要产生右侧这样一组对应的输出数据。

Input	Output
apple	eppli
cat	cet
utter	attor
finish	finish

我们来试着构建神经网络，并试着让它从这些词语中寻找出某种规律。你可能会问，如果是直接编程的话，我们可以使用很简单的方法就完成文字序列的转化，为什么要大费周章的用神经网络做这件事呢？

我们来提前看一个我准备在下一篇文章里介绍的应用。如果我们有几十万个用拉丁字母拼写的姓氏，我们需要在没有人为干预的情况下，让机器自动的根据姓氏拼写规则，把每一个姓氏归类到可能民族国家里，那这个工程显然是无法用手工编程完成的。

所以通过序列转化，我们会期望得到这样的输出：

Input	Output
Abbas	English
Addams	English
Brooks	English
Muirchertach	Irish
Neil	Irish
Ha	Korean
…	…

所以，为了有朝一日能做这样牛逼的模型出来，我们先来研究点简单的东西，看看它是如何做到的。

使用独热向量进行编码（One-Hot Vectors）

这是学习机器学习很容易接触到的最简单的编码形式，因为计算机不仅无法直接理解图像信息、也无法理解文字信息，所以这要求我们把计算机无法理解的数据都要预先处理成某种计算机可以理解的形式，而这一过程称为“编码”。

具体来说，以字母 ‘A’ 来举例，计算机是无法理解A的具体含义。但是如果用ASCII编码的形式表示A，比如用数字65表示A，计算机就可以理解这是什么意思。对于机器学习来说，类似的编码技术还有很多，这里我们使用一种名为 One-Hot-Vector 的编码来对字母进行重新编辑。

OHV 在中文圈里被称为独热向量，我个人是不太喜欢这样的名字，不是很直观。Hot在英文里有激活的含义，所以 One-Hot 被按照字面意义进行了翻译，那么我们不禁要问：“独热，那么谁热了？”

我们做一个简单的示例来说明这是如何编码的，以A，B，C，D进行举例，它们的 One-Hot 就可以表示为如下的形式：

字母	0位	1位	2位	3位
A	1	0	0	0
B	0	1	0	0
C	0	0	1	0
D	0	0	0	1

如果我们把 One-Hot 扩展到全部的大小写字母，那么上面这张表的有效数字列数就有52列，行数自然也是52行。

这固然是比较低效的编码方式，不过对于我们初学者来说是十分通俗易懂的。现在我们来做一个简单的程序片段，把文字转换成我们想要的形式：

常规的ASCII字符，从[a-zA-Z] 一共有52个，不过对于一个构造非常简单的RNN节点来说，它是没办法处理这么多信息的。所以我们只能构造一个非常非常简单的序列 。。。。。。

$$(h,e,l,o)$$

import torch
import string

all_letters = "helo"
n_letters = len(all_letters)


# Find letter index from all_letters, e.g. "a" = 0
def _letter_to_index(letter):
    return all_letters.find(letter)


def line_to_one_hot_tensor(line, max_padding=0):
    """
    Turn a line into a one-hot based tensor (character, one-hot-vector)
    """
    if max_padding >= len(line):
        tensor = torch.zeros(max_padding, 1, n_letters)
    else:
        tensor = torch.zeros(len(line), 1, n_letters)

    for idx, letter in enumerate(line):
        tensor[idx][0][_letter_to_index(letter)] = 1
    return tensor


def line_to_tensor(line, max_padding=0):
    """
    Turn a line into a ascii based tensor (character)
    """
    if max_padding >= len(line):
        tensor = torch.zeros(1, max_padding, dtype=torch.long)
    else:
        tensor = torch.zeros(1, len(line), dtype=torch.long)

    for idx, letter in enumerate(line):
        tensor[0][idx] = _letter_to_index(letter)

    return tensor.view(-1, 1)

现在我们随便输入一个单词，比如 ‘auo’，它输出的张量维度是

torch.Size([3, 1, 4])

维度为什么要这样定义，主要是对于 NLP (Natural Language Processing) 来说，默认的数据维度为

$$(Sequence,Batch,Inputs)$$

• Sequence - 字符串数组的长度
• Batch - torch 的 mini batch 大小
• Inputs - 又或是Input Features，这里指 One-Hot 的大小

准备数据集

要想让网络模型运作起来，我们还需要构建自己的数据集，正如前面已经提到过，我们需要通过打乱序列表的对应顺序来构建自己的数据集。不过显然，我们可以把目标字符串定义简单点。

def line_to_chaos_tensor(line: str, padding=0):
    if padding == 0:
        tensor = torch.zeros(1, len(line), dtype=torch.long)
    else:
        tensor = torch.zeros(1, padding, dtype=torch.long)

    for idx, char in enumerate(line):
        if char == 'h':
            tensor[0][idx] = _letter_to_index('h')
            continue
        if char == 'e':
            tensor[0][idx] = _letter_to_index('o')
            continue
        if char == 'l':
            tensor[0][idx] = _letter_to_index('l')
            continue
        if char == 'o':
            tensor[0][idx] = _letter_to_index('o')
            continue

    return tensor.view(-1, 1)

这个变化规律其实就是当语言序列中出现了e的时候，要变成o这么简单，当然你也可以在上面基础上测试其他的变化规则。

然后一个直接把文字序列直接转换为张量的方法，这样可以便于我们进行数据比对

def line_to_tensor(line, max_padding=0):
    """
    Turn a line into a ascii based tensor (character)
    """
    if max_padding >= len(line):
        tensor = torch.zeros(1, max_padding, dtype=torch.long)
    else:
        tensor = torch.zeros(1, len(line), dtype=torch.long)

    for idx, letter in enumerate(line):
        tensor[0][idx] = _letter_to_index(letter)

    return tensor.view(-1, 1)

接下来，我们做一个例子看看，看看能不能把字符转换串转换成我们想要的样子。

构建网络模型

这里我们直接使用 torch.nn.RNNCell 来完成这个工作，而不是用之前的那个线性模型。

torch.nn.RNNCell

来看看使用说明¹：

torch.nn.RNNCell(input_size, hidden_size, bias=True, nonlinearity=‘tanh’, device=None, dtype=None)

这里我们需要关注的就是 input_size 和 hidden_size 两项参数。

• input_size – The number of expected features in the input x
• hidden_size – The number of features in the hidden state h

RNNCell 是最基础的运算单元，我们在一次计算过程中，输入到网络的数据项长度为 (1, 57) 即1个字符，但是字符的编码是由57位长的One-Hot向量组成的。输出的数据长度也是57，但是意义发生改变，即 [0, 56] 序列上各元素的概率。

这样说你可能更明白一些，比方我们在某时刻输入的字符是 A，它的 One-Hot 表达是这样的

$$Input=(1,0,0,0)$$

经过RNNCell处理后，输出的 Output 是每一个元素的可能概率，

$$Output=(.2,.3,.0,.5)$$

这时如果计算损失函数，我们给出的值比如说是 2 (即第三位元素才是正确的答案)，对于网络来说它给出的第四位元素是就是错误的了，因此反向传播时，就会修正对四位的相关参数。

由于我们输出的数据也是对应5个分类，所以网络的输入和隐藏层大小就定义如下了。

HIDDEN_SIZE = 5
INPUT_SIZE = 5

接下来就是对网络的封装

import torch


class RNNCellModel(torch.nn.Module):

    """
    input_size – The number of expected features in the input x
    hidden_size – The number of features in the hidden state h
    bias – If False, then the layer does not use bias weights b_ih and b_hh. Default: True
    nonlinearity – The non-linearity to use. Can be either 'tanh' or 'relu'. Default: 'tanh'
    """

    def __init__(self, input_size, hidden_size):
        super().__init__()

        self.input_size = input_size
        self.hidden_size = hidden_size

        self.cell = torch.nn.RNNCell(input_size=self.input_size,
                                     hidden_size=self.hidden_size)

    def forward(self, data, hidden=None):
        """
        Forward computation

        @param data: (batch, input_size), tensor containing input features
        @param hidden: (batch, hidden_size), tensor containing the initial hidden state for each element in the batch.
        Defaults to zero if not provided.
        @return: (batch, hidden_size), tensor containing the next hidden state for each element in the batch

        """
        hidden = self.cell(data, hidden)
        return hidden

    def init_hidden(self, batch_size=1):
        return torch.zeros(batch_size, self.hidden_size)

这个没啥好说的，你直接抄就行。

RNNCell 的工作原理

我们在前面的章节内容中已经说过，RNN网络在每一次计算时，会通过隐藏层带入上一次的计算结果，如果把RNN网络展开后，一个基本的RNN节点的计算过程就是下面这样的

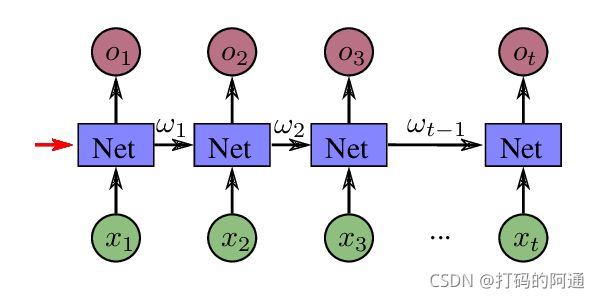
红色箭头指向的，就是第一次计算时，要传入给RNNCell的隐藏层 ${\omega }_0$，在我们这个例子中由于不存在先验知识（比方说需要对图片进行处理后提取特征等数据），所以这个输入可以是全0的张量，张量大小为

$$(batchSize,hiddenSize)$$

然后我们开始准备输入的 $x_i$，如果我们要让RNN网络处理的是字符串，那么每一次输入的就是字符串里被编码的字符，以 apple 为例

Input Sequence	Letter	One-Hot
$x_1$	a	(1, 0, 0, 0)
$x_2$	p	(0, 1, 0, 0)
$x_3$	p	(0, 1, 0, 0)
$x_4$	l	(0, 0, 1, 0)
$x_5$	e	(0, 0, 0, 1)

然后每执行一次RNNCell，它就会产生一个概率集合，例如 $x_1$ 作为输入时，就会产生一个对应的概率集合 $O_1$

如果是对序列进行变化，那么就需要在每次迭代的过程中处理一次损失函数，从而保证网路模型的收敛。此外，还有另外一种情况，如果我们仅需要处理的是分类问题，那么就需要在模型输出的最后部分处理相应的损失了。

因此，对于上面这个模型，它又等价于这个样子：

对于我们这个例子来说，当然是要处理每一个输出了，所以我们选择第一种方案。

定义数据集和训练过程

这里我直接把主体代码贴上来，如果你是从我前面的资料看过来的，相信你能看明白训练过程在做什么

BATCH_SIZE = 1
INPUT_SIZE = n_letters
HIDDEN_SIZE = n_letters

DATA = "hellolele"

# prepare data and labels
inputs = line_to_one_hot_tensor(DATA)
labels = line_to_chaos_tensor(DATA)

# define the network
model = RNNCellModel(INPUT_SIZE, HIDDEN_SIZE)

# update and criterion methods
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.1)

# train the network
for epoch in range(30):
    loss = 0

    optimizer.zero_grad()
    hidden = model.init_hidden()

	# feed data and label to the model
    for input, label in zip(inputs, labels):
        hidden = model(input, hidden)
        loss += criterion(hidden, label)

	# update the parameters
    loss.backward()
    optimizer.step()

然后我们再写一个测试，最后运行一下：

def test(model, data):
    print("Test {} to ".format(data), end='')

    with torch.no_grad():
        # convert the name to one-hot vector
        data = line_to_one_hot_tensor(data)

        # generate predicated values
        hidden = model.init_hidden()

        # send letter one by one to the model
        for i in range(data.size()[0]):
            x_data = data[i][0].view(1, -1)
            output = model(x_data, hidden)

            _, idx = torch.max(output, dim=1)
            print(decode_to_char(idx.item()), end='')

        print("")

运行结果是

Epoch 0 predicated string hleeehlll loss=11.72. Test hellolele to hllllllll
Epoch 1 predicated string hlllololo loss=9.06. Test hellolele to llllollll
Epoch 2 predicated string llllololo loss=7.72. Test hellolele to lollololo
Epoch 3 predicated string llllololo loss=6.91. Test hellolele to lollololo
Epoch 4 predicated string lollololo loss=6.26. Test hellolele to oollololo
Epoch 5 predicated string oollololo loss=5.69. Test hellolele to hollololo
Epoch 6 predicated string hollololo loss=5.23. Test hellolele to hollololo
Epoch 7 predicated string hollololo loss=4.86. Test hellolele to hollololo
Epoch 8 predicated string hollololo loss=4.53. Test hellolele to hollololo
Epoch 9 predicated string hollololo loss=4.26. Test hellolele to hollololo
Epoch 10 predicated string hollololo loss=4.04. Test hellolele to hollololo
Epoch 11 predicated string hollololo loss=3.88. Test hellolele to hollololo
Epoch 12 predicated string hollololo loss=3.75. Test hellolele to hollololo
Epoch 13 predicated string hollololo loss=3.65. Test hellolele to hollololo
Epoch 14 predicated string hollololo loss=3.56. Test hellolele to hollololo
Epoch 15 predicated string hollololo loss=3.48. Test hellolele to hollololo
Epoch 16 predicated string hollololo loss=3.42. Test hellolele to hollololo
Epoch 17 predicated string hollololo loss=3.37. Test hellolele to hollololo
Epoch 18 predicated string hollololo loss=3.33. Test hellolele to hollololo
Epoch 19 predicated string hollololo loss=3.30. Test hellolele to hollololo

---

1. https://pytorch.org/docs/stable/generated/torch.nn.RNNCell.html?highlight=torch%20nn%20rnncell#torch.nn.RNNCell ↩︎