局部线性嵌入算法(LLE)与其Python实现
PCA是至今为止运用最为广泛的数据降维算法,它通过最小化重构误差达到将高维数据映射到低维并同时保留数据中所存在的绝大部分信息。但是一般的PCA也有缺点,它只能实现线性降维。当然现在也有kernel PCA可以实现非线性降维,但我们今天介绍的是另一种实现非线性降维的算法——局部线性嵌入(Local Linear Embedding),其是基于流形学习的思想。
一、流形学习(Mainfold Learning)
流形学习是基于流形的思想,其认为现实世界中的高维数据集都可以用低维的流形所代替,而流形一般指高维空间中的几何结构,如曲线或曲面在高维空间中的推广,其是一个空间而不是面。所以直观上来讲,一个流形好比是一个d维的空间,在一个m维的空间中(m>d)被扭曲之后的结果。可以通过Python在三维空间中绘制简单的流形:
#%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import proj3d
#Generate mainfold data set
from sklearn.datasets import make_swiss_roll
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
axes = [-11.5, 14, -2, 23, -12, 15]
#plot figure
fig = plt.figure(figsize=(6, 5))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap=plt.cm.hot)
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
ax.set_xlim(axes[0:2])
ax.set_ylim(axes[2:4])
ax.set_zlim(axes[4:6])
plt.show()
可以看到,虽然数据集是在三维空间中的,但是我们完全可以通过一定的方法将其平铺在二维空间中并同时保存其数据结构。最简单的方法就是将卷曲的带状数据集拉直,如下图:
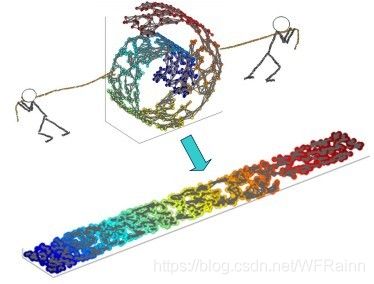
而这时如果想通过PCA将数据进行降维,效果将会非常差,因为你很难能够找到一个线性的平面将数据很好的进行投影,我们可以通过以下代码对比两种方法:
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], c=t, cmap=plt.cm.hot)
plt.axis(axes[:4])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$x_2$", fontsize=18, rotation=0)
plt.grid(True)
plt.subplot(122)
plt.scatter(t, X[:, 1], c=t, cmap=plt.cm.hot)
plt.axis([4, 15, axes[2], axes[3]])
plt.xlabel("$z_1$", fontsize=18)
plt.grid(True)
plt.show()

左边是将数据投影在xy平面上的结果,而右边是按照上图所示拉直数据集得到的结果。可以看到右边的降维效果远远好于左边。
基于流形与流形学习的思想,我们可以对数据进行非线性的降维,常见的方法有局部线性嵌入,拉普拉斯特征映射,局部保持投影,等距映射等。
二、局部线性嵌入(LLE)
LLE的基本思想如下,数据集X中每个样本 x i \mathrm{x}_{i} xi都可以通过与其邻近的几个样本近似的线性重构,用公式表示为:
x i ≈ ∑ j w i j x j \mathrm{x}_{i} \approx \sum_{j} w_{i j} \mathrm{x}_{j} xi≈j∑wijxj
其中j为与 x i \mathrm{x}_{i} xi相近的j个邻居。这样,求解如下的优化问题就可以得到重构系数:
ε ( W ) = ∑ i ∥ x i − ∑ j w i j x j ∥ 2 \varepsilon(\mathrm{W})=\sum_{i}\left\|\mathrm{x}_{i}-\sum_{j} w_{i j} \mathrm{x}_{j}\right\|^{2} ε(W)=i∑∥∥∥∥∥xi−j∑wijxj∥∥∥∥∥2
∑ j w i j = 1 \sum_{j} w_{i j}=1 j∑wij=1
得到重构系数后,将数据集X映射低维空间Y中,要保持同样的重构关系:
Φ ( Y ) = ∑ i ∥ y i − ∑ j w i j y j ∥ 2 \Phi(Y)=\sum_{i}\left\|y_{i}-\sum_{j} w_{i j} y_{j}\right\|^{2} Φ(Y)=i∑∥∥∥∥∥yi−j∑wijyj∥∥∥∥∥2
这样,我们便可以将流形铺开到低维空间中。通过求解上述优化问题就可以得到映射后的数据集Y。
三、算法推导
高维状态下重构系数的计算
设数据集X中样本个数为m,样本维数为n,映射后的数据集Y中样本维数为d,d<
J ( W ) = ∑ i = 1 m ∥ x i − ∑ j = 1 k w i j x j ∥ 2 2 J(W)=\sum_{i=1}^{m}\left\|x_{i}-\sum_{j =1}^{k} w_{i j} x_{j}\right\|_{2}^{2} J(W)=i=1∑m∥∥∥∥∥xi−j=1∑kwijxj∥∥∥∥∥22
∑ j k w i j = 1 \sum_{j}^{k} w_{i j}=1 j∑kwij=1
通过 ∑ j k w i j = 1 \sum_{j}^{k} w_{i j}=1 ∑jkwij=1,我们可以对优化函数进行化简:
J ( W ) = ∑ i = 1 m ∥ x i − ∑ j k w i j x j ∥ 2 2 = ∑ i = 1 m ∥ ∑ j k w i j x i − ∑ j k w i j x j ∥ 2 2 = ∑ i = 1 m ∥ ∑ j k w i j ( x i − x j ) ∥ 2 2 = ∑ i = 1 m W i T ( x i − x j ) T ( x i − x j ) W i \begin{aligned} J(W) &=\sum_{i=1}^{m}\left\|x_{i}-\sum_{j }^{k} w_{i j} x_{j}\right\|_{2}^{2} \\ &=\sum_{i=1}^{m}\left\|\sum_{j}^{k} w_{i j} x_{i}-\sum_{j }^{k} w_{i j} x_{j}\right\|_{2}^{2} \\ &=\sum_{i=1}^{m}\left\|\sum_{j }^{k} w_{i j}\left(x_{i}-x_{j}\right)\right\|_{2}^{2} \\ &=\sum_{i=1}^{m} W_{i}^{T}\left(x_{i}-x_{j}\right)^{T}\left(x_{i}-x_{j}\right) W_{i}\end{aligned} J(W)=i=1∑m∥∥∥∥∥xi−j∑kwijxj∥∥∥∥∥22=i=1∑m∥∥∥∥∥j∑kwijxi−j∑kwijxj∥∥∥∥∥22=i=1∑m∥∥∥∥∥j∑kwij(xi−xj)∥∥∥∥∥22=i=1∑mWiT(xi−xj)T(xi−xj)Wi
其中 W i = ( w i 1 , w i 2 , … w i k ) T W_{i}=\left(w_{i 1}, w_{i 2}, \dots w_{i k}\right)^{T} Wi=(wi1,wi2,…wik)T,为k维列向量, [ x i − x j ] = [ x i − x 1 , x i − x 2 , … , x i − x K ] \left[x_{i}-x_{j}\right]=\left[ \begin{array}{llll}{x_{i}-x_{1}} , {x_{i}-x_{2}},&{\dots} &, {x_{i}-x_{K}}\end{array}\right] [xi−xj]=[xi−x1,xi−x2,…,xi−xK],为n*k维矩阵。
我们令 Z i = ( x i − x j ) T ( x i − x j ) Z_{i}=\left(x_{i}-x_{j}\right)^{T}\left(x_{i}-x_{j}\right) Zi=(xi−xj)T(xi−xj),则上式可写成:
J ( W ) = ∑ i = 1 m W i T Z i W i J(W)=\sum_{i=1}^{m} W_{i}^{T} Z_{i} W_{i} J(W)=i=1∑mWiTZiWi对于重构系数的约束条件可以化为矩阵形式: ∑ j = 1 k w i j = W i T 1 k = 1 \sum_{j =1}^{k} w_{i j}=W_{i}^{T} 1_{k}=1 ∑j=1kwij=WiT1k=1。到此,我们便得到了化简后的优化函数,通过拉格朗日乘子法构造损失函数:
m i n L ( W ) = ∑ i = 1 m W i T Z i W i + λ ( W i T 1 k − 1 ) minL(W)=\sum_{i=1}^{m} W_{i}^{T} Z_{i} W_{i}+\lambda\left(W_{i}^{T} 1_{k}-1\right) minL(W)=i=1∑mWiTZiWi+λ(WiT1k−1)
对损失函数进行求导并令其值为0以求极值点:
2 Z i W i + λ 1 k = 0 2 Z_{i} W_{i}+\lambda 1_{k}=0 2ZiWi+λ1k=0
W i = λ ′ Z i − 1 1 k W_{i}=\lambda^{\prime} Z_{i}^{-1} 1_{k} Wi=λ′Zi−11k
其中 λ ′ = − 1 2 λ \lambda^{\prime}=-\frac{1}{2} \lambda λ′=−21λ是一个常数,对权重进行归一化得到最后的重构系数:
W i = Z i − 1 1 k 1 k T Z i − 1 1 k W_{i}=\frac{Z_{i}^{-1} 1_{k}}{1_{k}^{T} Z_{i}^{-1} 1_{k}} Wi=1kTZi−11kZi−11k
降维
在得到了高维状态下的重构系数后,我们现在将数据向低维映射,同时保留原有的重构关系:
J ( y ) = ∑ i = 1 m ∥ y i − ∑ j = 1 m w i j y j ∥ 2 2 J(y)=\sum_{i=1}^{m}\left\|y_{i}-\sum_{j=1}^{m} w_{i j} y_{j}\right\|_{2}^{2} J(y)=i=1∑m∥∥∥∥∥yi−j=1∑mwijyj∥∥∥∥∥22
此时,我们已知w,所求解的优化目标为y。为了简化运算,我们定义m*m维矩阵W,其中如果样本j为样本i的k个邻居之一,则 W i j \mathrm{W}_{ij} Wij为重构系数,而如果非其k个邻居之一,则 W i j = 0 \mathrm{W}_{ij}=0 Wij=0,这也是上式中第二个求和项的数目为m的原因。
同时,为了得到标准化的低维数据,我们对y做如下规定:
∑ i = 1 m y i = 0 ; 1 m ∑ i = 1 m y i y i T = I \sum_{i=1}^{m} y_{i}=0 ; \frac{1}{m} \sum_{i=1}^{m} y_{i} y_{i}^{T}=I i=1∑myi=0;m1i=1∑myiyiT=I
因此,优化函数可以简化为如下式:
J ( Y ) = ∑ i = 1 m ∥ y i − ∑ j = 1 m w i j y j ∥ 2 2 = ∑ i = 1 m ∥ Y I i − Y W i ∥ 2 2 = tr ( Y ( I − W ) ( I − W ) T Y T ) \begin{aligned} J(Y) &=\sum_{i=1}^{m}\left\|y_{i}-\sum_{j=1}^{m} w_{i j} y_{j}\right\|_{2}^{2} \\ &=\sum_{i=1}^{m}\left\|Y I_{i}-Y W_{i}\right\|_{2}^{2} \\&=\operatorname{tr}\left(Y(I-W)(I-W)^{T} Y^{T}\right)\end{aligned} J(Y)=i=1∑m∥∥∥∥∥yi−j=1∑mwijyj∥∥∥∥∥22=i=1∑m∥YIi−YWi∥22=tr(Y(I−W)(I−W)TYT)
其中, Y I i Y I_{i} YIi与 Y W i Y W_{i} YWi分别为矩阵相乘后的第i列。
此时,令 M = ( I − W ) ( I − W ) T M=(I-W)(I-W)^{T} M=(I−W)(I−W)T,则优化函数可以简写为 J ( Y ) = tr ( Y M Y T ) J(Y)=\operatorname{tr}\left(Y M Y^{T}\right) J(Y)=tr(YMYT),约束条件可以化为 Y Y T = m I Y Y^{T}=m I YYT=mI。同样,通过拉格朗日乘子法,损失函数可以写成下式:
m i n L ( Y ) = tr ( Y M Y T + λ ( Y Y T − m I ) ) minL(Y)=\operatorname{tr}\left(Y M Y^{T}+\lambda\left(Y Y^{T}-m I\right)\right) minL(Y)=tr(YMYT+λ(YYT−mI))
对其进行求导并取0得到:
2 M Y T + 2 λ Y T = 0 2 M Y^{T}+2 \lambda Y^{T}=0 2MYT+2λYT=0
M Y T = λ Y T M Y^{T}=\lambda Y^{T} MYT=λYT
此时,要求得最小的d维数据集,我们只需要对M矩阵求特征值与特征向量,并取其特征值最小的d个特征向量所组成的矩阵即可。
四、LLE的Python实现
接下来,可以通过Python的sklearn实现简单的LLE算法:
#Generate data
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=41)
from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_reduced = lle.fit_transform(X)
plt.title("Unrolled swiss roll using LLE", fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
plt.ylabel("$z_2$", fontsize=18)
plt.axis([-0.065, 0.055, -0.1, 0.12])
plt.grid(True)
save_fig("lle_unrolling_plot")
plt.show()

LLE的实现是基于流形的假设,如果数据集的分布并非流形,则其算法的降维效果可能并不会很出色。在实际运用中,我们可以首先使用原数据集进行机器学习的建模,再通过sklearn包中的GridSearchCV遍历不同的降维算法,查看模型的效果。
参考:
[1]Hands-On Machine Learning with Scikit-Learn and TensorFlow,东南大学出版社
