线段树+树状数组详解（1）

首先我们先来看一道题：

【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 $x$

• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 $x$ 个数加上 $k$

• 2 x y 含义：输出区间 $[x,y]$ 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

样例输出 #1

14
16

提示

【数据范围】

对于 $30\%$ 的数据，$1\le n\le 8$，$1\le m\le 10$；
对于 $70\%$ 的数据，$1\le n,m\le 10^4$；
对于 $100\%$ 的数据，$1\le n,m\le 5\times 10^5$。

样例说明：

故输出结果14、16

分析

本题有三种方法解决：
1.暴力
2.线段树
3.树状数组
我们今天重点介绍线段树的解法，我们先来看直接暴力：

暴力70TLE

#include
using namespace std;
int n,m,i,j,a,b,c,u[500004],s;
int main(){
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(i=1;i<=n;i++){
		cin>>u[i];
	}
	for(i=1;i<=m;i++){
		cin>>a>>b>>c;
		if(a==1)
			u[b]+=c;
		else {
			for(j=b;j<=c;j++){
				s+=u[j];
			}
			cout<<s<<endl;
			s=0;
		}	
	}
}

接下来，我们进入今天的重点：

线段树

首先，我们说线段树是一种高级数据结构，但他其实并不是一棵树，他是用结构体数组所实现的一颗“假树”，就是说，认为的把他的形态拉伸为一棵树，其实他在计算机看来只是一个打乱的顺序的线性结构：
线段树的知识点大概分为：
1.结构体数组
2.结构体下标计算
3.线段树的范围及继承关系（[l,r])
4.线段树区间查找
5.线段树单点修改

结构体数组的要素（仅限线段树）：l—左端点，r—右端点
sum—序列和
线段树是有结构体数组实现的，而非树形结构
线段树的内部结构是结构体数组

线段树的下标（Node[i]值）

线段树初始化时只有叶节点有value值，每一个非叶节点的value值
等于他左右子节点的value值之和，除叶节点外，每一非叶节点的左子
节点的下标（因为是数组）是他的父节点的1/2，即Lson=root<<1,右结点
是父节点的1/2+1，也是其兄弟结点+1值，即Rson=root<<1+1||Lson+1;

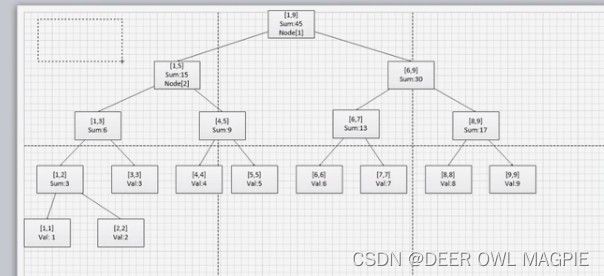
线段树的范围

线段树的范围指的是在l,r之间的序列，根结点的序列范围就是这全部元素
而非叶节点的左结点的范围是[root(l),mid=root(l)+root®<<1],所以，从某
种角度来讲线段树是一颗完全二叉树。
线段树的查找

单点修改：

每一次从根结点开始比较，如果需要比较的下标<=oot(l)+root®<<1,也就是
mid值，就往左分支走，知道l=r时停止并执行相应操作，否则前往右分支。
而，每一个节点都有所对应的sum值，当我们修改了子节点后，我们要不断向上
修改他父节点以及祖先的值，因为他的祖先的范围一定包含他所在的范围，这样的话
都需要随之修改。则单点修改复杂度O（logn).

区间查找：

区间查找的规则和单点修改一样，只不过遇到当前l=目标l，当前r=目标r
是即刻停止，此节点的sum值就是所要查找的值。

树状数组——概念讲解

树状数组顾名思义就是一个像树一样的数据结构，当然，和线段树一样，他的内部存储也是有规律的，只不过没有那么的明显，就如此图：

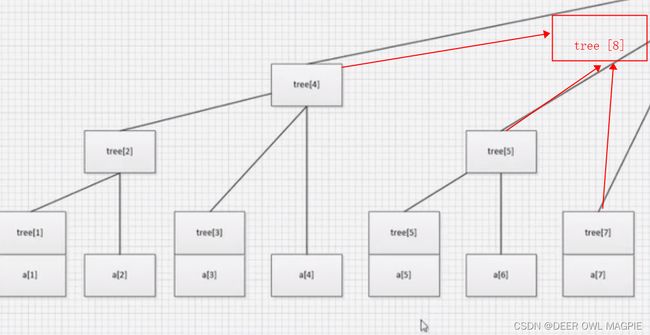
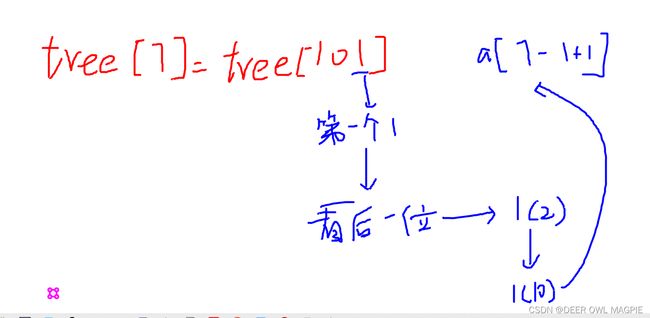
乍看发现不了什么规律，揣测不出这些线条是怎样连上的，这时，我们可以注意他的二进制转换，如下图：

这时我们关注红色的字体，我们发现，括号里的第一项a[x-y+1]中x就是当前树的下标，而他减去的红色字体，就是左边第二行得出的二进制数从右往左看第一个1和他之后的0所组成的数字，就如：6的二进制是110，从右往左看第一个1在第二位，所以我们只看后两位，得出10,10的十进制为4，所以减去4。如果这样解释您没看懂的话，就看下图：

此文会经常修改，持续更新