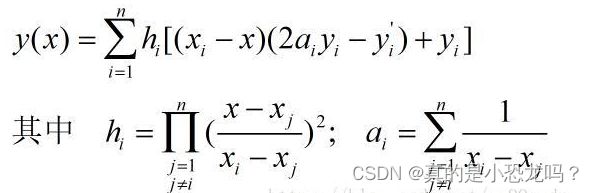【数值分析/计算方法】插值法及其余项MATLAB仿真实验
1、Lagrange插值法
方法:对给定的n个插值节点x1,x2,⋯,xn以及它们对应的函数值y1,y2,⋯,yn,利用构造的n-1次Lagrange插值多项式,可以通过下面式子求得插值区间内任意x的函数值。
Matlab实现:
function y = lagrange(x0,y0,x)
n=length(x0); %记录插值节点个数
m=length(x); %记录插值点个数
for i=1:m
z=x(i);
s=0.0;
for k=1:n
p=1.0;
for j=1:n
if(j~=k)
p=p*(z-x0(j))/(x0(k)-x0(j)); %连乘
end
end
s=s+p*y0(k); %求和
end
y(i)=s;
end2、Newton插值法
方法:通过选取特殊的基函数来实现
根据插值条件和差商定义,从而可以得到满足插值条件的n项插值多项式
Matlab实现:
function [A,y]= Newton(x0,y0,x)
% Newton插值函数
% x0为已知数据点的x坐标
% y0为已知数据点的y坐标
% x为插值点的x坐标
% 函数返回A差商表
% y为各插值点函数值
n=length(x0); m=length(x);
for t=1:m
z=x(t); A=zeros(n,n);A(:,1)=y0';
s=0.0; y=0.0;
for j=2:n
for i=j:n
A(i,j)=(A(i,j-1)- A(i-1,j-1))/(x0(i)-x0(i-j+1));
end
end
for k=1:n
p=1.0;
for l=1:k-1
p=p*(z-x0(l));
end
s=s+A(k,k)*p;
end
ss(t)=s;
end
y=ss;
A=[x0',A];
end3、Hermite插值法
方法:在实际问题中,不但要求在节点上函数值相等,而且往往会要求导数值也相等,即:
已知n个插值点x1,x2,⋯,xn及对应的函数值y1,y2,⋯,yn和一阶导数值y1′,y2′,⋯,yn′。则可以通过下面式子求得插值区间内任意x的函数值y
Matlab实现:
function [y,Rn]=Hermite_Re(x0,x)
%这里只讨论n个插值节点及其对应的函数值和一阶导数都存在,
%则每个插值节点都是函数的"二重节点"
syms t;
f=log(t);
y0=subs(f,t,x0);
y1=subs(diff(f,t),t,x0);
n=length(x0);
m=length(x);
for k=1:m
p=0.0;
for i=1:n
h=1.0;
a=0.0;
w=1.0;
for j=1:n
w=w*(x(k)-x0(j));
if (j~=i)
h=h*((x(k)-x0(j))/(x0(i)-x0(j)));
a=a+1/(x0(i)-x0(j));
end
end
p=p+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i));
end
y(k)=eval(p);
Rn(k)=diff(f,t,(2*n))/factorial(2*n)*w^2;
end
end4、分段低次插值
方法:通过插值点用折线或者低次的曲线连接起来逼近原曲线,规避Runge现象,可以通过调用Matlab内部函数interp1函数实现
一维数据插值指令,该指令可以对插值区间内的数据计算内插值,找出一元函数在插值点的数值
调用格式:vq=interp1(x,v,xq,'method') ; vq = interp1(x,v,xq,method,extrapolation)
其中x,v为已知的插值节点及其对应的函数值,xq为给定的插值点,vq为在插值点xq处的插值结果,extrapolation用于指定外插策略,来计算落在 x 域范围外的点。
‘method’表示采用的插值方法,Matlab内部提供了几种插值方法,常见的有:
-
‘linear’表示线性插值
-
‘nearest’表示邻近插值
-
'pchip'表示三次Hermite插值
-
…………
当method缺省时,默认表示线性插值。
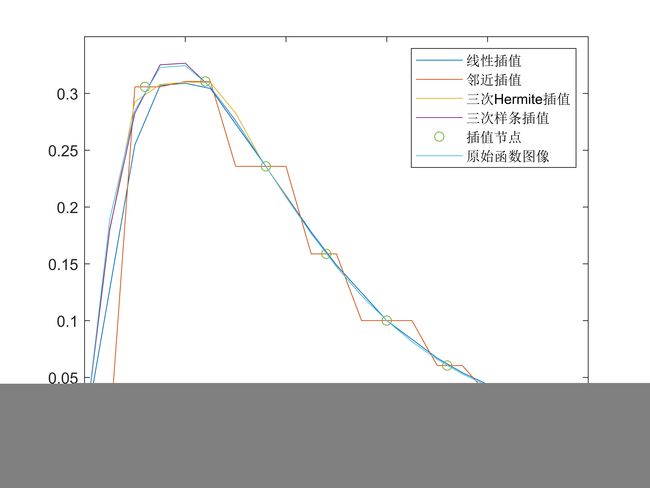
示例
x=0:0.12:1;
y=(x.^2-3*x+5).*exp(-5*x).*sin(x);
x1=0:0.05:1;
y0=(x1.^2-3*x1+5).*exp(-5*x1).*sin(x1);
y1=interp1(x,y,x1,'linear');%线性插值
y2=interp1(x,y,x1,'nearest');%最近点插值
y3=interp1(x,y,x1,'pchip');%三次Hermite插值
plot(x1,[y1',y2',y3'],x,y,'o',x1,y0);
legend('线性插值','邻近插值','三次Hermite插值','插值节点','原始函数图像')5、样条插值
方法:插值出来的函数不仅要连续,还要光滑。
在Matlab中,可以通过调用内部函数spline来实现三次样条数据插值
调用格式:s = spline(x,y,xq)
返回与 xq 中的插值点对应的插值 s 的向量。s 的值由插值节点 x 及其对应 y 的三次样条插值确定。
示例
x=0:0.12:1;
y=(x.^2-3*x+5).*exp(-5*x).*sin(x);
xq=0:0.05:1;
s=spline(x,y,xq);
plot(x,y,'o',xq,s); 将三次样条插值与分段插值进行对比,可以看出,三次样条插值曲线更加贴近原始函数图形,插值效果最好。
将三次样条插值与分段插值进行对比,可以看出,三次样条插值曲线更加贴近原始函数图形,插值效果最好。
下一步,可以在这些已有程序的基础上,根据各种插值方法的余项估计公式,编写程序,以分析各类插值法的误差估计。有兴趣的小伙伴可以持续关注本频道。如果你觉得写的不错的话,还请点赞转发收藏。