CS236 Deep Generative Models （1）基础介绍

一、概念介绍

1.1 概念定义

假设数据样本$X$，数据标签为$Y$，数据都来自一个真实分布$p(x)$，现在我们需要通过这些观测数据$X$拟合一个模型分布$q(x)$，使其接近真实分布$p(x)$.

• 生成(Generation)：从真实分布生成数据

• 推断(Inference)：从数据推断真实分布的参数或结构

• Prior Knowledge：在Deep Generative Model中的先验
  1. 损失函数(loss function)：如最大似然函数
  2. 参数形式(parametric form)：如假设真实分布服从正态分布
  3. 优化算法(optimization algorithm)

• 判别式与生成式的区别：

1. 判别式(Discriminative)：对条件概率$p(y|x)$建模，即在数据的真实分布空间中找出Decision Boundary，给定数据x属于标签y的概率
2. 生成式(Generative)：对联合概率$p(x,y)$建模，即尝试拟合一个数据与label共存的空间，得同时给定数据x和标签y，才能知道概率
3. 由Bayes有$p(y|x)=\frac{p(x,y)}{p(x)}$，Discriminative建模对象是$p(y|x)$(假设了参数结构、loss、优化方式等prior knowledge），所以模型只能接受输入$x$。但Generative是对$p(x,y)$建模，假设了联合分布的prior knowledge，如果知道y，它可以输出$p(x,y)=p(x|y)p(y)$；如果知道x，它也可以输出$p(x,y)=p(y|x)p(x)$，所以更全面也更复杂。
4. 于是Discriminative可以看作是一种Data Conditional Generative Model即$p(y|x)$，这区别于Class Conditional Generative Model即$p(x|y)$

1.2Deep Generative Model的三大问题

• Representation：
  如何对联合分布$p(x,y)$进行建模，怎样表示这个模型？
• Learning：
  如何准确地度量真实分布与模型分布的距离？（从而使其更接近）
• Inference：
  如何从观测数据中推断出真实分布的结构或者参数？

二、基本问题

2.1 Naive Bayes for Classification

• 需求：一封邮件进行分类，用标签变量$Y$描述，定义$Y=1$为垃圾邮件，$Y=0$为正常邮件

• 建模思路：设定一个大小为$n$的Vocabulary，令$x_i(i=1,2,...,n)$表示随机变量，如果邮件存在Vocabulary中的第$i$个词，则$x_i=1$。

• 生成模型：建模$p(Y,x_1,x_2,...,x_n)$

• 加一个先验：
  用一个箭头表示，条件独立性假设，如下图，受$Y$的影响，$x_i$与$x_j$条件独立，即$p(x_i,x_j|y)=p(x_i|y)p(x_j|y)$
  

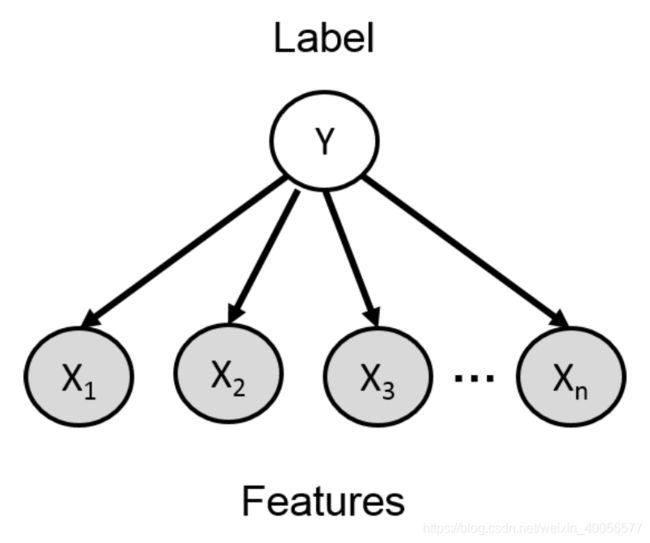
• Representation：
  $$p(y,x_1,...,x_n)=p(y)\prod _{i=1}^{n}p(x_i|y)$$

• Inference：
  $$\begin{array}{rl}p(Y=1|x_1,...,x_n)& =\frac{p(Y=1,x_1,...,x_n)}{p(x_1,...,x_n)}\\ & =\frac{p(Y=1){\prod }_{i=1}^{n}p(x_i|Y=1)}{{\sum }_{Y=0,1}p(Y=y){\prod }_{i=1}^{n}p(x_i|Y=y)}\end{array}$$

• Learning：
  从数据集$\{(X_1,Y_1)...(X_N,Y_N)\}$中学习模型参数，此处相当于在数据集中统计得：

  • $p(x_i|Y=1),i=1,...n$ 垃圾邮件vocabulary词频
  • $p(x_i|Y=0),i=1,...n$ 正常邮件vocabulary词频

所以，对于一个邮件$X_{new}=(x_1,x_2,...,x_n)$，用Inference中的$p(Y=1|x_1,...,x_n)$推断属于垃圾邮件的概率。

这就是Naive Bayes从生成式的角度看，对$p(X,Y)$联合建模，引入假设，当然此处省略了实际实现中的平滑、加log等trick，只是简单从生成式角度描述朴素贝叶斯问题并进行建模。

上图可从朴素贝叶斯角度看生成式与判别式，上面描述了对生成式的建模$P(X,Y)$，需要假设$P(X|Y)$的条件独立性，而如果是判别式的话，只需要直接建模$p(Y|X)$，如将X随便丢进一个分类器（Linear Regression），输出一个binary variable。

2.1 一般问题

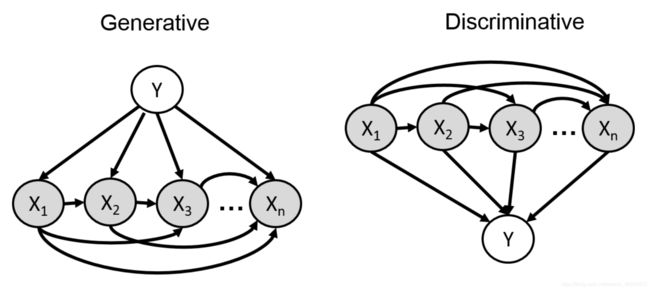
上面从Generative角度解决在Naive Bayes的问题，假设了条件独立性；
如果不加这个假设的一般问题如上左图所示，描述一下：

$$p(Y,X)=p(Y)p(X_1|Y)p(X_2|Y,X_1)\cdots p(X_n|Y,X_1,...,X_{n-1})$$
对于生成式，$p(Y)$很容易建模，但对于$p(X_i|X_{pa(i)},Y)$应该怎么建模比较好？($X_{pa(i)}$指其它指向$X_i$的所有结点施加的条件约束）

判别式描述如下：
$$p(Y,X)=p(X_1)p(X_2|X_1)\cdots p(Y|X_1,X_2,...,X_n)$$

因为$X$是完全可观测的数据，因此只需要把其丢到一个分类器如Logistic Regression就好了，如
$$\begin{gathered} p(Y=1|X_1,X_2,...,X_n)=\sigma ({\alpha }_0+\sum _{i=1}^n{\alpha }_i{X}_i) \\ \sigma (z)=\frac{1}{1-e^{-z}} \end{gathered}$$

那什么时候需要生成式模型？
当观测数据并非完全可观测的时候，即$X=(X_1,X_2,...,X_n)$中可能有些维度如$X_h$是隐藏的，观测不到的，就需要使用生成模型解决问题，只需要把$p(X|Y)$中观测不到的维度求积分或求和去掉就好。

三、不同类型的Network

3.1 Bayes Net

Bayesian Network 由一个有向无环图(Directed Acyclic Graph)确定，即G=(V,E)

• 一个结点node $i\in V$代表一个随机变量$X_i$
• 一个node受到有向edge的约束，其条件概率分布表示为$p(x_i|x_{pa(i)})$，也称为BN factors
• 联合分布为：
  $$p(x_1,...,x_n)=\prod _{i\in V}p(x_i|x_{pa(i)})$$
  
  对于一个具体的有五个随机离散变量的Bayesian Network：
  

$$\begin{array}{rl}由p(x_1,...,x_n)& =\prod _{i\in V}p(x_i|x_{pa(i)})\\ p(x_1,...,x_n)& =p(x_1)p(x_2|x_1)\cdots p(x_n|x_1,...,x_{n-1})\\ 得p(d,i,g,s,l)& =p(d)p(i)p(g|i,d)p(s|i)p(l|g)\\ p(d,i,g,s,l)& =p(d)p(i|d)p(g|d,i)p(s|d,i,g)p(l|d,i,g,s)\end{array}$$

从而知道了Bayesian Network中的条件独立性，即$d\perp i,s\perp \{d,g\}|i,l\perp \{d,i,s\}|g$

3.2 Neural Models

Logistic Regression看成对features的linear transformation，Neural Models看成对features的Nonlinear transformation，是一个判别式模型。假设现在有四个随机变量$X_1,X_2,X_3,X_4$从概率角度看：

• Chain Rule
  $$p(X_1,X_2,X_3,X_4)=p(X_1)p(X_2|X_1)p(X_3|X_1,X_2)p(X_4|X_1,X_2,X_3)$$

链式法则是最General联合分布分解。

• Bayesian Network
  $$p(X_1,X_2,X_3,X_4)\approx p(X_1)p(X_2|X_1)p(X_3|X_1,X_2)p(X_4|X_1,X_2,X_3)$$

贝叶斯网络是对随机变量之间进行了条件假设。

• Neural Models
  $$p(X_1,X_2,X_3,X_4)\approx p(X_1)p(X_2|X_1)p_{Neural}(X_3|X_1,X_2)p_{Neural}(X_4|X_1,X_2,X_3)$$

神经网络则是对条件假设采取了特殊的函数形式近似。

3.3 连续变量的Generative Model

在3.1的Bayes Net中，构建了一个离散随机变量的Bayesian Network。
但当随机变量是连续的时候，就不能用一个表列举了，只能采用概率密度函数进行表示。

• 一个离散随机变量$Z$与一个连续随机变量的联合分布$X$
  • $Z\sim Bernouli(p)$
  • $X|Z=0\sim N(u_0,{\sigma }_0),X|Z=1\sim N(u_1,{\sigma }_1)$
  • p(z,x)=p(z)p(x|z)
• 两个随机变量的联合分布(VAE的形式)
  • $Z\sim N(0,1)$
  • $X|Z=z\sim N(u_{\theta }(z),{\sigma }_{\varphi }(z))$