”AE-OT A NEW GENERATIVE MODEL BASED ON EXTENDED“阅读笔记

"AE-OT A NEW GENERATIVE MODEL BASED ON EXTENDED SEMI-DISCRETE OPTIMAL TRANSPORT”阅读笔记

来源：ICLR 2020

链接：https://openreview.net/pdf?id=HkldyTNYwH

文中图像来自于上述论文及顾险峰微信公众号“老顾谈几何”。

1 论文概述

该论文对GAN和VAE生成图像出现的模式崩塌和模糊问题进行了分析，认为GAN和VAE会产生模式崩塌的直接原因是CNN，因为CNN只能拟合连续分布，而实际上的图像分布是离散的；同时，即使是针对单模态图像分布，假如图像分布的支撑集是非凸的，那CNN也没办法拟合出完整的图像分布，而会产生伪样本：

比如上面这张图，图a表示了在单一模态且支撑集为凸的数据分布上CNN的拟合效果，此时CNN可以正常拟合出数据分布；图b表示单模态且支撑集非凸时CNN的拟合效果，此时CNN会产生不属于数据分布的伪样本；图c显示了拟合多模态数据时的过程，红色虚线表示奇异点集，可以理解为是不同模态数据之间的分界，在理想情况下($f_3$)，只有位于这些奇异点集合上的噪声才会被映射为伪样本（红色×），而实际上CNN会倾向于产生模式崩塌($f_{31}$)和模式混合($f_{32}$)情况。

该论文认为图像生成过程分为流行嵌入和分布匹配两部分，第一部分是将高维/低维流形嵌入/反嵌入到低维/高维流形中，第二部分是实现标准噪声分布到离散图像数据分布的匹配。他们认为流形嵌入这一步可以交给CNN来做，而分布匹配应该由OT来完成。所以本论文将这两部分功能进行拆分，由自编码器实现流形嵌入工作，而设计了一个基于Brenier potential的OT凸优化过程来实现从标准噪声分布到低维嵌入空间的匹配，计算二者之间的最优传输。然后再拓展这个最优传输，使用类似插值的思想实现从噪声分布到生成图像的映射。

2 方法解读

2.1最优传输映射构建

这里的最优传输和传统最优传输的实现方式不太一样，是从几何角度进行逼近和解释的，如有兴趣，可以参阅顾险峰本人写的相关介绍文章。下面的内容尽可能从通俗角度进行解释，本人没有很深的数学功底，如有不严谨之处请见谅！

假定定义在欧氏空间中的一个区域为$\Omega \in {\mathbb{R}}^d$，其上有一个测度$\mu$，也就是我们通常定义的标准噪声分布，这个分布是连续的，同时，另有一个同样定义在$\Omega$上的测度$v$，是图像在$\Omega$上的支撑集，可以理解为图像经编码器提取到的特征嵌入分布。$v$是由若干个数据点构成的离散狄拉克测度：

$\mu$和$v$之间是保测的：

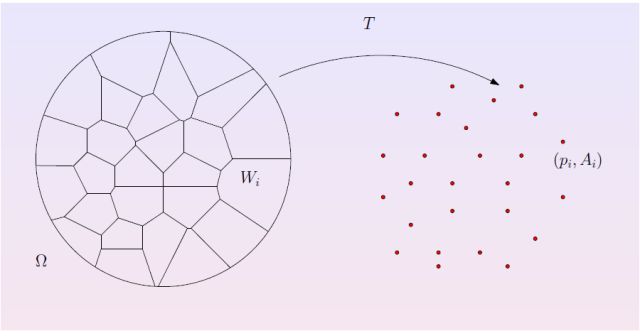
我们希望构建一个传输映射$T$，使得$\mu$可以映射到$v$，使总成本最小的传输映射称为最优传输映射：

从几何角度来看，这个问题相当于将一个平面$\mu$分解为$n$个区域，使得每一个区域$W_i$的面积$w_i=v_i$：

当选择传输损失为

时，最优传输映射是Brenier potential的梯度，在正则点上，Brenier potential是连续且可微的，其梯度也是连续的；而在奇点上，Brenier potential是连续不可微的，因此，在该点处的最优传输映射是不连续的。作者通过这一点，期望通过构建Brenier potential图，并计算梯度得到一个半离散（分段连续）的最优传输映射。从而解决CNN使用连续映射逼近不连续分布的问题。

从几何意义上对Brenier potential进行解释，假如$\mu (\Omega )$已知，其对应的Brenier potential的图是由若干平面${\pi }_i$的围成的开放凸多面体记为$u(x)=ma{x}_i(<x,y_i>+h_i)$，个人认为可以通俗理解为对Brenier potential就是对$x$进行聚类，将其划分到最接近$y_i$的簇，对于某个面${\pi }_i=<x,y_i>+h_i$，其梯度就是$y_i$，$\mu (\Omega )$的胞腔分解就是这若干个${\pi }_i$的投影，通过调整截距$h_i$的大小，我们就可以令$W_i$的面积$w_i=v_i$。

同时，$h$满足${\sum }_i{h}_i=0$。整个问题就转变成了通过求截距$h_i$，最终确定$\mu$的胞腔分解，从而将同属于某个胞腔中的数据映射为$y_i$，这个映射就是最优传输映射。

顾险峰团队提出了使用变分法求解$h$的算法，将胞腔面积记为$w_i(h)$，定义凸面能量函数为：

该函数有唯一的极值点，对$h$求偏导，得：

通过梯度下降法，求得导数为0的点，就是该问题的最优解。

对于该梯度，$v_i$已知，而$w_i(h)$未知，使用蒙特卡洛法进行采样实现估计，具体来说，就是随机从$\mu$中采样$N$个点，根据$u(x)=ma{x}_i(<x,y_i>+h_i)$对$x$进行聚类，$w_i$即为$x$被映射为第$i$类的比例，即$w_i(h)=N_i(x)/N$。

最开始时，令$h_i=0$，算法如下：

2.2 最优传输拓展

上面的最优传输构建出了从标准噪声分布$\mu$到图像嵌入分布$v$之间的映射，实现了从噪声到具体嵌入的变换过程，理论上，我们可以通过$T\cdot f(\mu )$实现图像生成，$f$为解码器。但这一过程无法生成图像样本之外的其他数据，作者提出，将不同胞腔分解的结果中心化，使用蒙特卡洛方法计算每个胞腔的均值$c_i$点，作为胞腔$W_i$的代表。然后，将相邻胞腔的中心点相邻，获得一张图（绿色的边所示），同时，通过边与边的相邻关系，可以得知$\mu$上的奇点集合（红色区域），对$v$上的点也进行相同操作，这样，可以通过插值，生成属于真实图像嵌入分布上的样本。

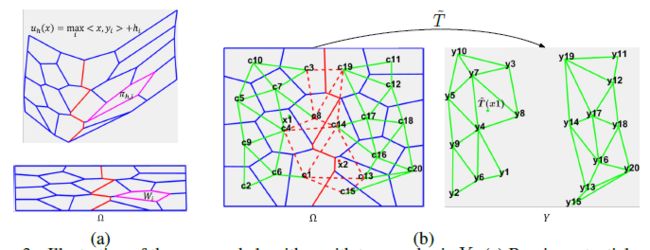
具体实现时，对于某个随机采样点$x$，计算其与所有胞腔中心的距离$d(x,c_i)$，选取距离最大的前$d$个点，将$x$用这$d$个点近似表示，每个点$c$对$x$的贡献权重为：

然后，令$T(x)$为：

为了避免$x$是奇点，需要对$x$在平面中的位置进行判断，但要在高维空间中构建出一张图比较困难，作者使用的方法是，假如两个平面$W_a,W_b$之间不相邻，这两个平面在Brenier potential上对应的平面${\pi }_a,{\pi }_b$的二面角会很大，因此，可以计算我们筛选出来的若干个胞腔中心$c_1,..,c_d$对应的平面${\pi }_1,...,{\pi }_d$两两之间的二面角${\theta }_{ij}$，若所有的二面角都大于某个阈值$\hat{\theta }$，那认为$x$是奇点，不应该生成图像，否则删除备选胞腔中心中不符合条件的所有胞腔中心，重新计算贡献权重，并得到最终的映射$T(x)$：

实际上这个阈值$\hat{\theta }$的选取对于模型性能的影响非常大，但这个选取也没有什么好的方法，只能在实验时一点一点试。

最终的实验结果为：

SEMI-DISCRETE%20OPTIMAL%20TRANSPORT%E2%80%9D%E9%98%85%E8%AF%BB%E7%AC%94%E8%AE%B0/5.png" />