What is torch.nn really?

我们建议在notebook上运行本教程，而不是脚本。

PyTorch提供了经过优雅设计的模块和torch.nn,torch.optim,Dataset,DataLoader类，来帮助你创建及训练神经网络。为了充分地利用它们的力量，并为解决你的问题而定制它们，你需要真正地明白它们是怎样工作的。为了促进你的理解，我们将会先不使用任何这些模块中的功能来在MNIST数据集上训练一个基本神经网络；我们在一开始只会使用PyTorch中最基本的张量功能。随后，我们将会逐步地一次一个地添加torch.nn,torch.optim,Dataset或DataLoader中的功能，来展示每个功能到底是干什么的，以及它到底是怎样让代码变得既简洁又灵活的。

MNIST data setup

我们将会使用经典的MNIST数据集，它包含了黑白的0-9的手写数字。

我们将会使用pathlib来处理路径(Python标准库中的一部分)，并且会使用requests来下载数据集。我们只会在使用模块时才引入它们，所以你可以确切地看到在每个部分上需要什么。

## Python中关于文件操作的库
## 见 https://blog.csdn.net/amanfromearth/article/details/80265843
from pathlib import Path
import requests

## 获得数据集地址
DATA_PATH = Path("data")
PATH = DATA_PATH / "mnist"

## 创建文件夹，parents为True时，则创建缺失的路径文件夹
## exist_ok在True忽略路径存在时的FileExistsError
## 见 https://majing.io/posts/10000007281150
PATH.mkdir(parents = True,exist_ok=True)

URL = "http://deeplearning.net/data/mnist"
FILENAME = "mnist.pkl.gz"

if not (PATH/FILENAME).exists():
    ## .content返回二进制数据，比如图片和文件
    content = requests.get(URL + FILENAME).content
    
    ## 将读取的图片写入路径的文件中
    (PATH / FILENAME).open("wb").write(content)

该数据集的格式为numpy数组，并使用python特有的序列化数据的方法pickle保存。

import pickle

## python的压缩和解压缩模块，可以读写gzip文件
## 见 https://www.cnblogs.com/liuzhang0223/p/7146253.html
import gzip

## open()打开gzip文件，as_posix()将地址的\\转化为/
## 见 https://docs.python.org/3/library/pathlib.html
with gzip.open((PATH / FILENAME).as_posix(),"rb")as f:
    ((x_train,y_train),(x_valid,y_valid),_) = pickle.load(f,encoding="latin-1")

(注：在这里我遇到了问题，这段代码运行后提示f不是gzip文件。于是我去一开始的代码提到的网址上直接下了图像并放在相应的路径上。我的猜测是可能是写入数据的函数有所变化，或gzip文件的格式变化了。)

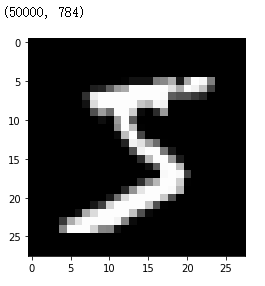
每个图片的大小为28 * 28，并且以一维行的形式存储，其长度为784(= 28 * 28)。我们可以从中挑出一幅图片看一看，不过看之前我们需要把它reshape为二维。

from matplotlib import pyplot
import numpy as np

pyplot.imshow(x_train[0].reshape((28,28)),cmap="grey")
print(x_train.shape)

其结果为：

PyTorch使用torch.tensor，而不是numpy数组，所以我们需要转换我们的数据。

import torch

x_train,y_train,x_valid,y_valid = map(torch.tensor,(x_train,y_train,x_valid,y_valid))
n,c = x_train.shape
x_train,x_train.shape,y_train.min(),y_train.max()

其结果为：

Neural net form scratch(no torch.nn)

让我们首先来创建一个只使用PyTorch的张量操作的模型。我们假设你已经熟悉了神经网络的主要内容。

PyTorch提供了创建由随机数或0填充的张量的方法，我们可以使用它们来创建一个简单的线性模型的权重和偏置。它们只是普通的张量，只有一点很特殊：我们告诉PyTorch它们需要梯度。这将会使PyTorch记录所有在这些张量上的操作，于是它可以在后向传播时自动地计算梯度。

对权重来说，我们在初始化后设置requires_grad，因为我们不想把初始化操作记录到梯度中。(注意_在PyTorch中表明该操作在原地进行。)
(注：原地操作即指用函数结果覆盖对应的值，而不是把结果存储在其它地方。)

import math

weights = torch.randn(784,10) / math.sqrt(784)
weights.requires_grad_()
bias = torch.zeros(10,requires_grad=True)

由于PyTorch自动计算梯度的能力，我们可以使用任何标准Python函数(或可调用的对象)来做模型。因此，接下来我们可以编写一个简单的矩阵乘法和广播加法(broadcasted addition)来创建一个简单的线性模型。我们也需要激活函数，所以我们要写一个log_softmax函数并使用它。记住：尽管PyTorch提供了很多预先写好的损失和激活等函数，但你可以使用简单地python轻松地写出你自己的函数。PyTorch甚至可以为你的函数自动地创建快速GPU或矢量化的CPU代码。

def log_softmax(x):
    
    ## unsqueeze()是squeeze()的逆操作，用于在指定维增加维度
    ## 见 https://blog.csdn.net/flysky_jay/article/details/81607289
    return x - x.exp().sum(-1).log().unsqueeze(-1)

def model(xb):
    return log_softmax(xb @ weights + bias)

上方的@表示点乘操作。我们将会在一批数据上调用我们的函数(在本教程中，为64幅图像)。这是一个前向传播。注意在这种情况下，我们的预测不会比随机猜好多少，因为我们的权重开始是随机值。

bs = 64

xb = x_train[0:bs]
preds = model(xb)
preds[0],preds.shape

其结果为：

如你所见的，preds张量包含的不仅是张量值，还有梯度函数。我们将在之后的后向传播中使用该函数。

接下来我们将部署一个负对数似然函数来作为损失函数(我们依然可以只用标准python来实现这一点)。

## 因为preds每一行的10个数据分别表示了对该行对应的图像属于该列对应的类的概率的对数值
## 而概率属于[0,1]，且每行概率和为1，因此preds中每行对应的图象所属的类对应的列的值(该
## 值为概率的对数值)的负数，能够反映预测值与真实值的偏离大小，即误差的大小。而从整体
## 的角度考虑，再对所有的误差取平均(这里我觉得取和，取乘等也行)。
def nll(input,target):
    return -input[range(target.shape[0]),target].mean()

loss_func = nll

接下来让我们看一下我们的随机模型的误差值，从而使我们明白我们是否能在接下来的后向传播中进行改进。

yb = y_train[0:bs]
print(loss_func(preds,yb))

其结果为：

接下来我们实现一个计算我们模型的预测精度的函数。对preds的每行数据来说(其代表了一幅图像属于每个类的概率的对数值)，如果其最大值所在的列数与该行对应的类相同，我们就可以认为预测正确。

def accuracy(out,yb):
    
    ## 返回每行最大值的index，见 https://www.jianshu.com/p/cf7adeff2a05
    preds = torch.argmax(out,dim=1)
    return (preds == yb).float().mean()

让我们看看我们的随机模型的准确度，这样我们就能知道在改善了误差后，判断的准确度能否提高。

accuracy(prebs,yb)

其结果为：

我们现在可以开始一个循环训练。对每次迭代，我们将会：

• 选择一小批量的数据(大小为bs)。
• 使用模型进行预测。
• 计算损失。
• 使用loss.backward()更新模型的梯度，在该例子中，即更新权重和偏置。

我们现在使用这些梯度来更新权重和偏置。我们在torch.no_grad()上下文管理器中执行此操作，因为我们不希望这些操作被记录到下次梯度的计算中去。

我们随后将梯度设为0，以便于进行下次循环。否则，我们的梯度将会记录已发生的所有操作的运行记录(也就是说，loss.backward()将会把梯度存储到所有保存的操作上去，而不是替换它们)。

TIP:
你可以使用标准python调试器来逐步执行PyTorch代码，这允许您在每一步都检查各种变量的值。取消注释下方代码中的set_trace()来尝试这种做法。

# IPython是一个类似jupyter notebook的交互式shell。有很多强大的功能
# 见 https://www.jianshu.com/p/3fbc3b481d1f
# set_trace()用于设置断点，以便调试
# 见 https://www.jianshu.com/p/0de8fc8c09ed
from IPython.core.debugger import set_trace

lr = 0.5
epochs = 2

for epoch in range(epochs):
    for i in range((n - 1) // bs + 1):
        # set_trace()
        start_i = i * bs
        end_i = start_i + bs
        xb = x_train[start_i:end_i]
        yb = y_train[start_i:end_i]
        pred = model(xb)
        loss = loss_func(pred,yb)
        
        loss.backward()
        with torch.no_grad():
            weights -= weights.grad * lr
            bias -= bias.grad * lr
            weights.grad.zero_()
            bias.grad.zero_()

完成了：我们完全从头开始创造并训练了一个最小的神经网络(在这个例子里，也可以称其为一个逻辑回归模型，因为我们并没有任何隐藏层)。

让我们检查下误差和准确度，并把它们与我们之前的结果相对比。我们希望误差能够下降，而准确度能够提升，结果表明确实是这样的。

loss_func(model(xb),yb),accuracy(model(xb),yb)

其结果为：

使用torch.nn.functional

我们现在要重构我们的代码，使得它能够利用PyTorch的nn类的优点，能够以更简洁和灵活的方式完成我们设定的任务。从这里开始的每一步，我们应当让我们的代码完成至少一项以下的目标：更短，更可理解，以及/或更灵活。

最开始且最容易的步骤是使用torch.nn.functional(一般导入命名空间F)中的激活和误差函数来代替我们手写的函数。该模块包含了所有torch.nn库中的函数(而该库的其他部分包含了类)。除了大量的误差和激活函数，你还能从这里找到一些能够方便地创建神经网络的函数，比如池化函数(还有做卷积、线性层等功能的函数，但是之后我们会提到，最好使用库的其它部分来做这些事)。

之前我们使用的负对数似然误差函数以及log softmax激活函数，PyTorch提供了一个简单的函数F.cross_entropy来将这两个函数统一。所以我们甚至可以将激活函数从我们的模型中移去。

import torch.nn.functional as F

loss_func = F.cross_entropy

def model(xb):
    return xb @ weight + bias

注意我们不会再调用log_softmax函数了。让我们首先确定我们的误差和准确度和之前一样：

loss_func(model(xb),yb),accuracy(model(xb),yb)

其结果为：

使用nn.Module进行重构

接下来，我们将会使用nn.Module和nn.Parameter，来进行更清晰和简洁的迭代训练。我们首先申明一个继承了nn.Module的子类(nn.Module本身是一个类，且它能够跟踪状态)。在这种情况下，我们想要创建一个保有我们的权重、偏置以及前向传播的方法的类。nn.Module有我们能用到的很多属性和方法(比如.parameters()和.zero_grad())。

Note:
nn.Module(注意M是大写)是PyTorch独有的概念，也是我们会频繁使用的类。不要把nn.Module与Python中的模块(m为小写)概念混淆，后者是可被导入的Python代码文件。

from torch import nn

class Mnist_Logistic(nn.Module):
    def __init__(self):
        super().__init__()
        self.weights = nn.Parameter(torch.randn(784,10) / math.sqrt(784))
        self.bias = nn.Parameter(torch.zeros(10))
        
    def forward(self,xb):
        return xb @ self.weights + self.bias

由于我们现在不再直接使用函数，而是使用了对象，我们就必须首先实例化我们的模型：

model = Mnist_Logistic()

现在我们可以使用和之前一样的方法来计算误差了。注意nn.Module对象使用的方法和函数一样(也就是说它们是可调用的)，但在幕后，PyTorch将自动调用我们的forward方法。

loss_func(model(xb),yb)

其结果为：

先前，我们在进行迭代训练时，我们必须按名称更新每个参数的值，并手动分别将每个参数的梯度置零，像这样：

with torch.no_grad():
            weights -= weights.grad * lr
            bias -= bias.grad * lr
            weights.grad.zero_()
            bias.grad.zero_()

但现在我们可以利用model.parameters()和model.zero_grad()(二者均被PyTorch的nn.Module定义)来使得这些步骤更简洁，且让我们更不容易忘记我们的某些参数——当我们有一个非常复杂的模型时，这就很有用了。

with torch.no_grad():
    for p in model.parameters():
        p -= p.grad * lr
    model.zero_grad()

我们将把我们小小的迭代训练放到fit函数里，以便我们后续使用：

def fit():
    for epoch in range(epochs):
        for i in range((n - 1) // bs + 1):
            start_i = i * bs
            end_i = start_i + bs
            xb = x_train[start_i:end_i]
            yb = y_train[start_i:end_i]
            pred = model(xb)
            loss = loss_func(pred,yb)
            
            loss.backward()
            
            with torch.no_grad():
                for p in model.parameters():
                    p -= p.grad * lr
                model.zero_grad()

fit()

让我们仔细检查一下，我们的误差是否已经下降：

loss_func(model(xb),yb)

其结果为：

使用nn.Linear重构

我们继续重构我们的代码。为了取代手动定义和初始化self.weights和self.bias，以及计算xb @ self.weights + self.bias，我们使用PyTorch的nn.Linear类，它能够帮我们完成以上这些工作。PyTorch有很多种能够极大地简化我们程序的预先定义的层，而且往往这些层能够加速运算。

class Mnist_Logistic(nn.Module):
    def __init__(self):
        super().__init__()
        self.lin = nn.Linear(784,10)
        
    def forward(self,xb):
        return self.lin(xb)

我们用与之前一样的方法来实例化我们的模型，以及计算误差：

model = Mnist_Logistic()
loss_func(model(xb),yb)

其结果为：

我们还可以像之前一样使用我们的fit():

fit()
loss_func(model(xb),yb)

其结果为：

使用optim进行重构

PyTorch还有一个有着许多优化算法的包：torch.optim。我们可以使用我们optimizer的step方法来进行前向传播，而不是手动地更新每个参数。

这将让我们取代之前的手动编码优化步骤：

with torch.no_grad():
    for p in model.parameters(): p -= p.grad * lr
    model.zero_grad()

并用以下代码代替：

opt.step()
opt.zero_grad()

（optim.zero_grad()把梯度重设为0，我们必要要在计算下个小批量数据之前调用它。）

from torch import optim

我们将要定义一个小函数来创建我们将来可以重新利用的的模型和optimizer：

def get_model():
    model = Mnist_Logistic()
    return model,optim.SGD(model.parameters(),lr=lr)

model,opt = get_model()
print(loss_func(model(xb),yb))

for epoch in range(epochs):
    for i in range((n - 1) // bs + 1):
        start_i = i * bs
        end_i = start_i + bs
        xb = x_train[start_i:end_i]
        yb = y_train[start_i:end_i]
        pred = model(xb)
        loss = loss_func(pred,yb)
        
        loss.backward()
        opt.step()
        opt.zero_grad()
        
print(loss_func(model(xb),yb))

其结果为：

使用Dataset重构代码

PyTorch有一个抽象的Dataset类。Dataset类有着__len__函数(被Python的标准len函数调用)以及用于按索引取数据的__getitem__函数。Data Loading and Processing教程提供了一个非常好的创建一个通用的Dataset的子类FacialLandmarkDataset的例子。

PyTorch的TensorDataset是一个Dataset包装了的张量。通过定义求长度和索引查找的方式，它也提供了迭代、索引以及沿张量的第一维切片的方法。这将使我们更容易在我们训练的同一行里同时访问独立和非独立变量。

from torch.utils.data import TensorDataset

x_train和y_train可以同时被同一到一个简单的TensorDataset中，以便于迭代和切分。

train_ds = TensorDataset(x_train,y_train)

先前，我们必须分别迭代x和y的minibatch：

xb = x_train[start_i:end_i]
yb = y_train[start_i:end_i]

现在，我们可以把这两个步骤整合为一个：

xb,yb = train_ds[i * bs:i * bs + bs]

model,opt = get_model()
print(loss_func(model(xb),yb))

for epoch in range(epochs):
    for i in range((n - 1) // bs + 1):
        xb,yb = train_ds[i * bs: i * bs + bs]
        pred = model(xb)
        loss = loss_func(pred,yb)
        
        loss.backward()
        opt.step()
        opt.zero_grad()
        
print(loss_func(model(xb),yb))

其结果为：

使用DataLoader重构代码

PyTorch的DataLoader负责管理batch。你可以从任何Dataset中创建DataLoader。DataLoader使得迭代batch更加容易。比起必须使用train_ds[i * bs: i * bs + bs]，DataLoader自动地给我们提供了每个minibatch。

from torch.utils.data import DataLoader

train_ds = TensorDataset(x_train,y_train)
train_dl = DataLoader(train_ds,batch_size=bs)

先前，我们要以如下方式迭代(xb,yb):

for i in range((n-1) // bs + 1):
	xb,yb = train_ds[i * bs: i * bs + bs]
	pred = model(xb)

现在我们的循环变得更干净了，因为(xb,yb)可以自动地从dataloader中加载：

for xb,yb in train_dl:
    pred = model(xb)

model,opt = get_model()

for epoch in range(epochs):
    for xb,yb in train_dl:
        pred = model(xb)
        loss = loss_func(pred,yb)
        loss.backward()
        
        opt.step()
        opt.zero_grad()
        
print(loss_func(model(xb),yb))

其结果为：

多谢PyTorch的nn.Module,nn.Parameter,Dataset和DataLoader，我们的循环训练现在变得更小，且更易理解。现在让我们试着添加在实践中创建有效模型所需的基本功能。

增加验证

在第一节中，我们只是尝试设置合理的训练循环以用于我们的训练数据。但在现实中，你总是应该有一个验证集，以确定你是否过拟合。

洗牌训练数据对于防止batch间的相关性及过拟合来说非常重要。除此之外，无论我们是否对验证集进行洗牌，验证误差都是相同的。由于洗牌花费了额外的时间，因此对验证数据进行洗牌是没有意义的。

我们将会使用batch size作为验证集，其大小为训练集的两倍。这是因为验证集不需要后向传播，因此它们需要更小的存储空间(它们不需要记录梯度)。我们利用了这点，从而可以使用一个更大的batch size，并更快地计算误差。

train_ds = TensorDataset(x_train,y_train)
train_dl = DataLoader(train_ds,batch_size=bs,shuffle=True)

valid_ds = TensorDataset(x_valid,y_valid)
valid_dl = DataLoader(train_ds,batch_size=2*bs,shuffle=False)

我们将会在每个epoch的末尾计算和打印验证集的误差。

(注意我们总是在训练前调用model.train()，在inference前调用model.eval()，因为这两个会被nn.BatchNorm2d和nn.Dropout等层使用来确保后者在不同的阶段(注：指训练和测试)有着更合适的行为。)

model,opt = get_model()

for epoch in range(epochs):
    model.train()
    for xb,yb in train_dl:
        pred = model(xb)
        loss = loss_func(pred,yb)
        
        loss.backward()
        opt.step()
        opt.zero_grad()
        
    model.eval()
    with torch.no_grad():
        valid_loss = sum(loss_func(model(xb),yb) for xb,yb in valid_dl)
    
    print(epoch,valid_loss / len(valid_dl))

其结果为：

创建fit()和get_data()

现在我们将会做一点小小的重构。由于我们经历了两次计算训练集和验证集误差的类似过程，接下来让我们把它放到我们自己的函数loss_batch()里，它可以计算一个batch的误差。

我们为训练集传递一个optimizer，并使用它来执行后向传播。对于训练集，我们不传递任何optimizer，所以该方法并不进行后向传播。

def loss_batch(model,loss_func,xb,yb,opt=None):
    loss = loss_func(model(xb),yb)
    
    if opt is not None:
        loss.backward()
        opt.step()
        opt.zero_grad()
        
    return loss.item(),len(xb)

fit运行了训练我们的模型和计算每个epoch的训练和验证误差的必要操作。

import numpy as np

def fit(epochs,model,loss_func,opt,train_dl,valid_dl):
    for epoch in range(epochs):
        model.train()
        for xb,yb in train_dl:
            loss_batch(model,loss_func,xb,yb,opt)
            
        model.eval()
        with torch.no_grad():
            
            # zip()将可迭代的对象作为参数，将对应的元素打包成元组，并返回
            # 由这些元组构成的列表。当各个迭代器的大小不一致，则按最短的返回。
            # zipped=zip(),*zipped表示将zipped解压回原来的列表。
            # 见 https://www.runoob.com/python/python-func-zip.html
            losses,nums = zip(*[loss_batch(model,loss_func,xb,yb) for xb,yb in valid_dl])
        
        val_loss = np.sum(np.multiply(losses,nums)) / np.sum(nums)
        
        print(epoch,val_loss)

get_data返回训练集和验证集的dataloader。

def get_data(train_ds,valid_ds,bs):
    return(
    DataLoader(train_ds,batch_size=bs,shuffle=True),
    DataLoader(valid_ds,batch_size=bs * 2)
    )

现在，我们获取dataloader和拟合模型的整个过程可以用三行代码运行：

train_dl,valid_dl = get_data(TensorDataset(x_train,y_train),
                             TensorDataset(x_valid,y_valid),bs)
model,opt = get_model()
fit(epochs,model,loss_func,opt,train_dl,valid_dl)

其结果为：

你可以以这三行代码为基础训练很多种模型。要我们看看能否使用它来训练一个卷积神经网络(CNN)。

切换至CNN

我们现在要构建一个有着三个卷积层的神经网络。因为之前章节的函数都没有限定模型的类型，我们可以不做修改地使用它们来训练一个CNN。

我们将会使用PyTorch预先定义的Conv2d类作为我们的卷积层。我们使用三个卷积层来定义CNN。每个卷积后都有一个ReLU。在最后，我们进行均值池化。(注意PyTorch的view就是numpy中的reshape)

class Mnist_CNN(nn.Module):
    def __init__(self):
        super().__init__()
        
        # Conv2d()是nn包的一个设定二维卷积层的函数，kernel_size为卷积核大小
        # stride是卷积的步长，padding是每个维度隐式填充的0。这三个值可以是
        # 元组，也可以是int，此时表示(int,int)。
        # 见 https://pytorch.org/docs/stable/nn.html
        self.conv1 = nn.Conv2d(1,16,kernel_size=3,stride=2,padding=1)
        
        self.conv2 = nn.Conv2d(16,16,kernel_size=3,stride=2,padding=1)
        self.conv3 = nn.Conv2d(16,10,kernel_size=3,stride=2,padding=1)
        
    def forward(self,xb):
        xb = xb.view(-1,1,28,28)
        xb = F.relu(self.conv1(xb))
        xb = F.relu(self.conv2(xb))
        xb = F.relu(self.conv3(xb))
        xb = F.avg_pool2d(xb,4)
        return xb.view(-1,xb.size(1))
    
lr = 0.1

momentum是随机梯度下降(stochastic gradient descent,SGD)的一个变量，它考虑了先前的更新，并通常使得训练更快。

model = Mnist_CNN()
opt = optim.SGD(model.parameters(),lr=lr,momentum=0.9)

fit(epochs,model,loss_func,opt,train_dl,valid_dl)

其结果为：

nn.Sequential

torch.nn还有一个我们能够用来简化我们的代码的便利的类：Sequential。Sequential对象以顺序方式运行它包含的每个模块。这是编写神经网络的一种更简单的方法。

要利用这一点，我们需要能够轻松地使用给定函数定义自定义图层。比如说，PyTorch没有view图层，我们需要自己创建一个。我们可以使用Lambda来创建一个，并在之后使用Sequential定义神经网络时使用它。

class Lambda(nn.Module):
    def __init__(self,func):
        super().__init__()
        self.func = func
        
    def forward(self,x):
        return self.func(x)

def preprocess(x):
        return x.view(-1,1,28,28)

使用Sequential创建的模型非常简单：

model = nn.Sequential(
    Lambda(preprocess),
    nn.Conv2d(1,16,kernel_size=3,stride=2,padding=1),
    nn.ReLU(),
    nn.Conv2d(16,16,kernel_size=3,stride=2,padding=1),
    nn.ReLU(),
    nn.Conv2d(16,10,kernel_size=3,stride=2,padding=1),
    nn.ReLU(),
    nn.AvgPool2d(4),
    Lambda(lambda x:x.view(x.size(0),-1))
)
    
opt = optim.SGD(model.parameters(),lr=lr,momentum=0.9)

fit(epochs,model,loss_func,opt,train_dl,valid_dl)

其结果为：

包装DataLoader

我们的CNN已经足够简洁了，但它只会在MNIST上运行，因为：

• 它假定输入为28 * 28的长向量
• 它假定最终的CNN格网大小是4 * 4(因为我们使用的平均池化核就是这么大)

让我们摆脱这两种假设，来让我们的模型能够运行任何2d单通道图像。首先，我们可以去除初始化Lambda图层，但将数据预处理放到生成器中。

def preprocess(x,y):
    return x.view(-1,1,28,28),y

class WrappedDataLoader:
    def __init__(self,dl,func):
        self.dl = dl
        self.func = func
        
    def __len__(self):
        return len(self.dl)
    
    def __iter__(self):
        batched = iter(self.dl)
        for b in batched:
            
            # yield是一个生成迭代器并返回值的关键字
            # 见 https://blog.csdn.net/mieleizhi0522/article/details/82142856
            yield(self.func(*b))

train_dl,valid_dl = get_data(train_ds,valid_ds,bs)
train_dl = WrappedDataLoader(train_dl,preprocess)
valid_dl = WrappedDataLoader(valid_dl,preprocess)

接下来，我们要用AdaptiveAvgPool2d来代替nn.AvgPool2d，因为它允许我们定义我们想要的output张量的大小，而不必定义我们有的input张量的大小。于是我们的模型可以运行任意大小的输入。

model = nn.Sequential(
    nn.Conv2d(1,16,kernel_size=3,stride=2,padding=1),
    nn.ReLU(),
    nn.Conv2d(16,16,kernel_size=3,stride=2,padding=1),
    nn.ReLU(),
    nn.Conv2d(16,10,kernel_size=3,stride=2,padding=1),
    nn.ReLU(),
    nn.AdaptiveAvgPool2d(1),
    Lambda(lambda x:x.view(x.size(0),-1))
)

opt = optim.SGD(model.parameters(),lr=lr,momentum=0.9)

让我们看看它的结果：

fit(epochs,model,loss_func,opt,train_dl,valid_dl)

其结果为：

使用你的GPU

如果你有能够使用CUDA的GPU(或从云服务商那里以大概3块钱每小时的价格租一个)，你可以使用它来加速你的代码。首先确定你的GPU可以在PyTorch中运行。

print(torch.cuda.is_available())

其结果为：

接着我们创建一个device对象：

dev = torch.device("cuda:0"if torch.cuda.is_available() else "cpu")

让我们更新下preprocess并把它移动到GPU上：

def preprocess(x,y):
    return x.view(-1,1,28,28).to(dev),y.to(dev)

train_dl,valid_dl = get_data(train_ds,valid_ds,bs)
train_dl = WrappedDataLoader(train_dl,preprocess)
valid_dl = WrappedDataLoader(train_dl,preprocess)

最后，让我们把我们的模型放到GPU上：

model = model.to(dev)
opt = optim.SGD(model.parameters(),lr=lr,momentum=0.9)

现在你运行起来应该快多了：

fit(epochs,model,loss_func,opt,train_dl,valid_dl)

我们现在有一个通用的数据管道和循环训练，你可以在PyTorch中使用它们来训练多种模型。要了解现在训练一个模型有多简单，请看mnist_sample示例notebook。

当然，还有很多你想添加的东西，比如说数据增强，超参数调整，监控训练和迁移学习等。这些功能在fastai库中可用，且已被以本教程同样的方法来展示，为希望进一步采用其它模型的从业者提供了自然的下一步。

我们在本教程的开始部分保证我们会逐个举例解释torch.nn,torch.optim,Dataset和DataLoader。下面让我们总结一下我们所学到的。

• torch.nn

  • Module:创建一个像函数一个可调用，但也可以包含状态(比如说神经网络的层权重)的类。它知道它包含哪些参数，并可以将它们的梯度全部归零，在循环中更新它们的权重。除此之外，它还有很多功能。
  • Parameter:张量的包装器，它告诉Module它拥有在后向传播中需要更新的权重。只有requires_grad设为True的张量会在后向传播中被更新。
  • functional:一个包含了激活、误差等函数以及层的模板——如卷积层和线性层，的模块(一般引入到命名空间F中)，

• torch.optim:包含了包括SGD在内的，在后向传播过程中更新Parameter权重的optimizer。

• Dataset:一个有着__len__和__getitem__的对象的抽象接口，包含了PyTorch提供的类，比如TensorDataset。

• DataLoader:将任意的Dataset作为输入，并创建迭代器，并以批次的方式返回数据。