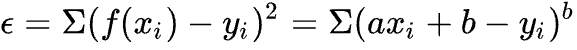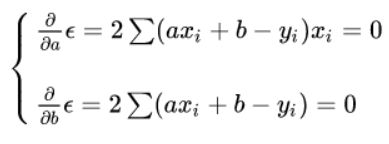CS131专题-4:拟合(最小二乘、RANSAC、霍夫变换)
本专题目的:了解最小二乘、RANSAC、霍夫变换这3个算法的基本原理,能够做到脱口而出,并从零编程实现。
目录
1 前言
2 最小二乘
2.1 基本原理
2.2 求解方法
3 RANSAC 算法
3.1 基本原理
4 霍夫变换
4.1 基本原理——检测直线
4.1.1 极坐标系
4.1.2 找到参数空间中交点密集位置的方法
4.1.3 一些效果图
4.2 基本原理——检测圆
4.3 霍夫变换的其他应用
5 总结
1 前言
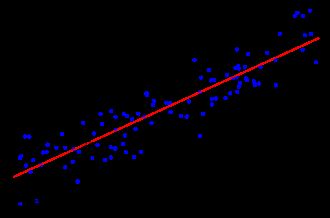
上一专题知道了如何提取图像中边缘像素,本专题我们看看如何从边缘图中,通过‘拟合’技术,来进一步提取一些我们需要的几何形状边缘,如直线、圆、或者其他形状。
当然,从图像中找到我们想要的一些几何特征,存在一些难点:
- 噪声:图像以及预处理会存在各种噪声,影响拟合。
- 外点(无关点):如果我们要找一辆车上的几何形状,那么图像中车之外的像素点都是无关像素,但它们会影响我们程序自动化寻找。
- 遮挡:目标图形部分被遮挡,使几何形状间断。
(备注:机器学习中也有算法可以完成此事,而且效果更好、更鲁棒,所以本专题不做太深入细究,且一些传统视觉算法的延伸优化问题也不介绍了)
2 最小二乘
2.1 基本原理
最小二乘法(least square method)是一种常用的数学优化方法,所谓二乘就是平方的意思。这平方一词指的是在拟合一个函数的时候,通过最小化误差的平方来确定最佳的匹配函数,所以最小二乘指的就是拟合的误差平方达到最小。
假设这种线性关系为:f(x) = ax+b
总误差的平方为:
在误差式子中,不同的 a,b 会导致不同的 E,根据多元微分的知识,当它们的偏微分等于0时,E 可取最小值。
上述方程组为线性方程组,求解上述方程组,得出 a,b 的值后,我们就能找到一条‘最佳’拟合线。(备注:其实这种距离判定方法并不是最优的,具体可见北邮鲁鹏的《计算机视觉》中一些最小二乘的改进方法)
2.2 求解方法
主要利用线性代数相关技巧:
本小节主要参考:http://mangoroom.cn/opencv/least-square-method-line-fit.html
3 RANSAC 算法
一眼就能明白,最小二乘拟合方法有太多局限性。效果受噪音数据、图像遮挡等很大影响。
- 普通最小二乘法是保守派:在现有数据下,如何实现最优。是从一个整体误差最小的角度去考虑,尽量谁也不得罪。
- RANSAC是改革派:首先假设数据具有某种特性(目的),为了达到目的,适当割舍一些现有的数据。
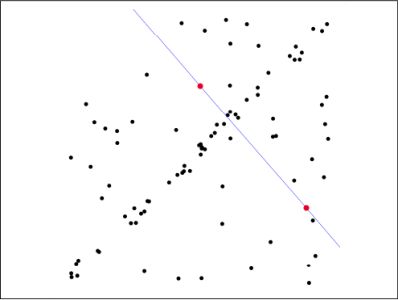
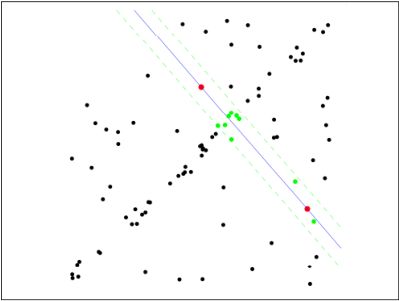
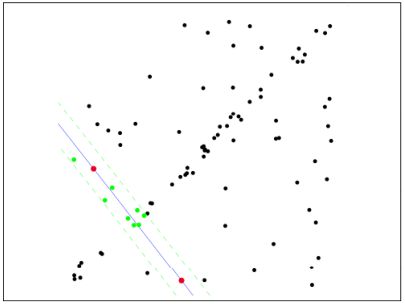
3.1 基本原理
RANSAC简化版的思路就是:
第1步:随机选择几个样本点(如估计一条直线方程需要两个点,其他模型可能不一样)
第2步:拟合出一个模型(即把这个直线方程定下来)
第3步:设置一个门限
第4步:记下门限内囊括的“内点”的数量,重复1~4步,迭代N次
第5步:最后选用那个“内点”最多的拟合模型。
RANSAC算法一个很重要参数是:迭代次数。这个参数有种方法可以估算大概是要多少。
具体原理和过程参考:
- RANSAC算法详解(附Python拟合直线模型代码) - 知乎
- RANSAC算法理解_robinhjwy的博客-CSDN博客
真实应用时,其实需要针对特定问题和情况做更多改进,比如RANSAC最终得到最好的一根线,其实再用最小二乘去拟合这根线周围的点,得到的新直线会更好。
4 霍夫变换
RANSAC不好解决图像中存在大量线的情况。
- 霍夫变换,可以用来检测图像中任意多个直线、圆、椭圆等几何体。它最初被设计成用来检测能够精确地解析定义的形状(即可以用数学公式精确定义的几何体)。后来广义霍夫变换(1972)不要求给出几何体的解析式。
- 它通过将图像坐标空间变换到参数空间,来实现直线与曲线的拟合。
4.1 基本原理——检测直线
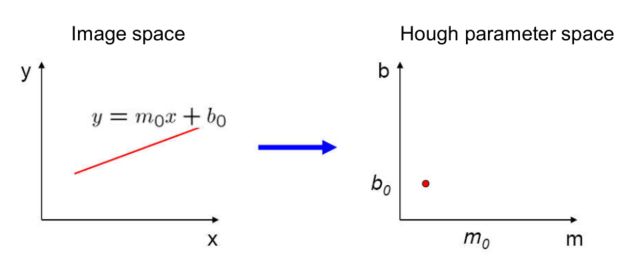
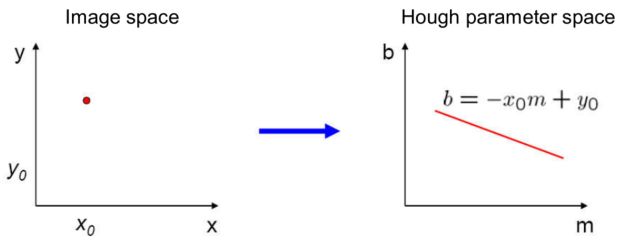
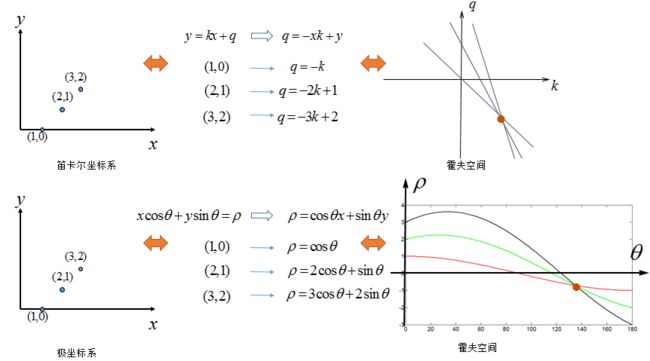
理解第1点:图像中的一条直线在参数空间(霍夫空间)是一个点:
原因:只要确定了m和b值,那么也就在 x,y 空间确定了一条直线。
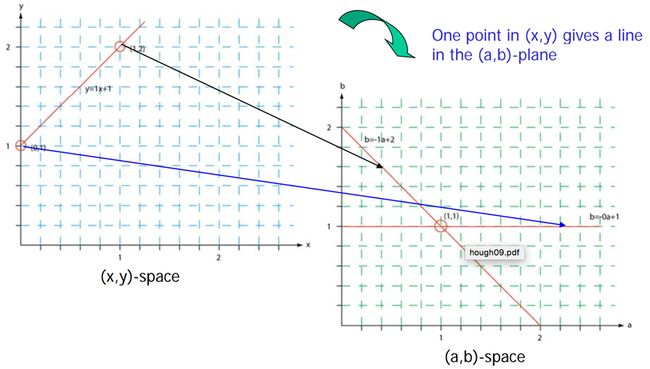
理解第2点:图像中,经过某点的无数条直线,在参数空间里可以用一条直线表示。(或者也可以说,图像空间中一个点,在参数空间中是一条直线)
原因:图像中经过某点的直线公式为 y0 = x0*m+b,而这个公式在参数空间就是一条直线。
理解第3点:参数空间中两条线的交点,代表图像空间中两个点的直线。
原因:参数空间中两条线交点位置的参数,可以在图像空间确定一条直线,而这条这些必定经过参数空间那两条直线所对应图像空间中那两个点。
理解第4点:将图像空间中所有点在参数空间用直线描述,然后将参数空间网格化,统计参数空间每个网格内的直线交点个数(也就是投票),交点数越多的,表示这个网格所对应的参数在图像空间所形成的直线更有可能是图像边缘所形成的直线。
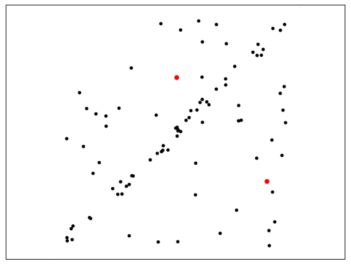
以下是图片中得票率(交点数)最高的20条直线:
理解上面4点,基本也就理解霍夫变换找直线的方法了,其实找圆也类似,只是直线参数空间变成圆方程参数空间。
当然,实际找直线时,并不是用 y = mx + b方程。原因是:
- 图像中垂直的直线,斜率无穷大,在参数空间中此交点位置会离原点无穷远。这导致没法计算了。
4.1.1 极坐标系
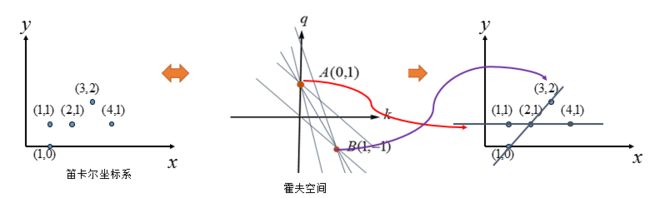
图像坐标是笛卡尔坐标系,我们把参数空间用极坐标中参数表示就能解决上述问题。
如下图,xy坐标系中任意一个点,可以用θ和ρ参数来表示:
要意识到两点:
- θ值仅在180个单位长度内就能完整的与图像空间中所有点进行对应。
- ρ值其实也是有限大的,因为图像尺寸是长宽的,也即xy长度有限,那么根据极坐标转换公式,ρ也不会无限大。
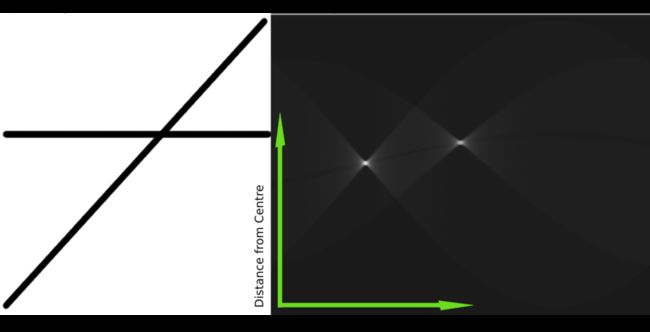
把θ和ρ作为参数,则图像空间中一个点,在参数空间中就变为一条正弦曲线,如下图:
上图,我们的θ在0~180直接,也可以画在-90~90之间。
4.1.2 找到参数空间中交点密集位置的方法
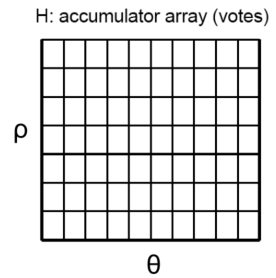
首先我们网格化参数空间,只要统计出每个网格内有多少根线经过,就也算出了该网格所对应的参数值在边缘图像空间中形成的直线,是会经过多少个边缘像素点。
我们用一个二维矩阵 H 来代表参数空间:
具体算法过程如下:
- 将二维数组(作为累加器) H(θ, ρ) 初始化为0
- For 图像空间每个像素点(x, y)
- For θ 0到180
- 计算ρ值:(ρ = x*cosθ + y*cosθ)
- 投票+1(因为此θ和ρ点有条线经过):H(θ, ρ) = H(θ, ρ) + 1
- End
- For θ 0到180
- End
- 寻找H矩阵中,元素值的局部波峰位置,这些位置所对应θ和ρ值,就对应图像中各边缘形成的直线。
注意:
- 由于图像中的直线往往具有一定的像素宽度,这会导致 H 矩阵的局部会有连续几个高投票值位置,因此每找到一个当前最大的峰值点后,需要将该点及其附近点清零,以防算法检测出多条极其邻近的“假”直线。
- 具体使用时,还是要应对噪声问题,也可以借助图像中梯度方向来减少遍历次数等等,具体要用时还是要更深入研究。
4.1.3 一些效果图
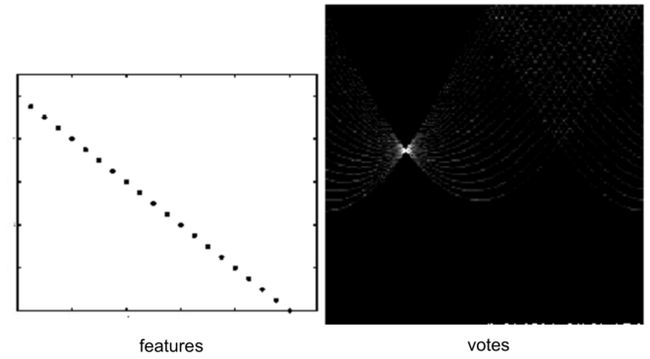
散点线:
有噪声的情况:
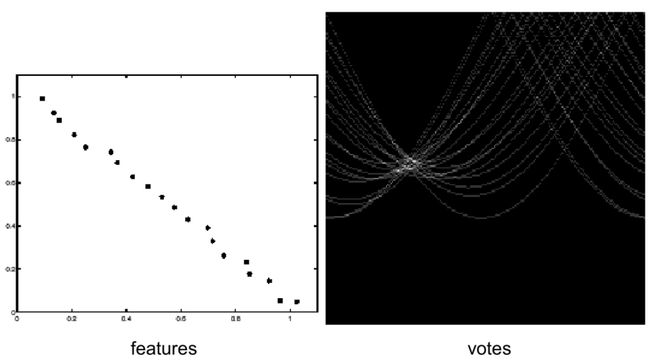
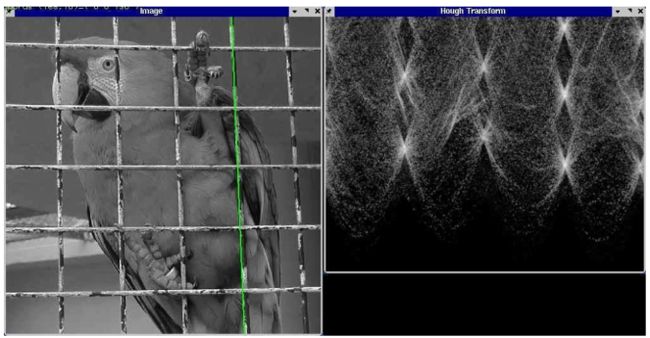
两根粗直线:
上图左边是一个边缘图像,每个像素点通过极坐标映射到霍夫空间后,会有2个密集交汇区,而且这个高亮区宽度还是比较大的(代表边缘图像中大量平行且临近的直线)。
正方形和圆:
上图正方形霍夫空间会有4个交汇点,而圆没有任何密集交汇区(上图亮度只是可视化方式不一样)。
几何图形在一起情况:
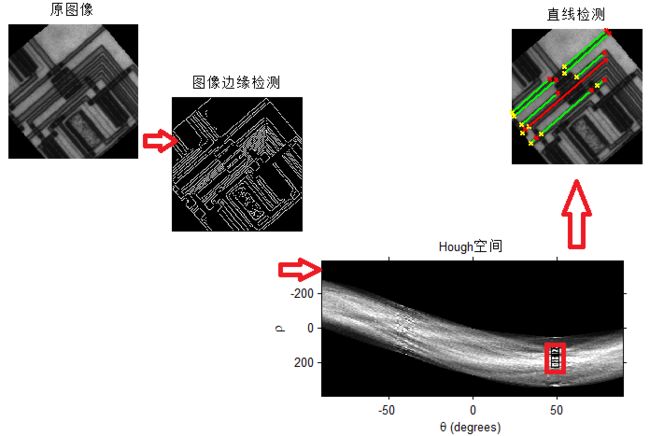
电路板:
网格线:
4.2 基本原理——检测圆
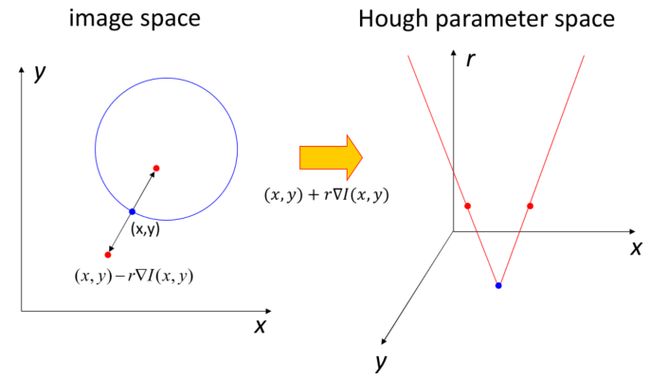
根据下面的图,理解如下几点:
- 图像中一个圆,可以用三个参数表示:圆心坐标(x, y)和半径 r ,所以,图像中一个圆,可以用三维参数空间中一个点来表示。
- 图像中一个点,它如果在图像中的某个圆上,那它和圆心所成的方向,是该点图像梯度的方向!(图像梯度的原理和计算方法见专题2)。这一点很重要,这是理解后续的基础,也是该建模方法可穷举投票的理由。(当然,残缺了一点的圆,这些残缺像素位置梯度可能为0或其他,但并不影响后续投票算法)
- 基于已知的某点图像梯度方向,经过图像中某一个点的所有可能的圆,可以在x,y,r三维空间中用两根直线表示。(如果不考虑该点梯度方向,则笛卡尔坐标系中某一个点,其所有可能的圆,在参数空间中可以用一个立体圆锥曲面表示!)
- 对于图像中某个像素点 (x,y) ,当给定r半径值后,仅有两个可能的圆心位置(这两个潜在可能的圆心位置相对这个像素点互为镜像位置),这两个圆心的位置可以通过x,y,r,以及图像梯度角度值计算出来。
理解上述4点后,遍历图像中每个像素点,再遍历r长度的可能范围,通过投票来找,找到参数空间中密度高亮区,这些位置的参数就锁定了图像中一些圆。算法如下:
- For 图像中每一个边缘像素点
- For r in range( len(最大半径) )(注意:r是可穷举的,因为图像中最大的完整圆,其半径最大为图像高或宽的一半)
- 计算圆心坐标(a, b)
- H(a, b, r) = H(a, b, r) + 1
- End
- For r in range( len(最大半径) )(注意:r是可穷举的,因为图像中最大的完整圆,其半径最大为图像高或宽的一半)
- End
- 找出H(a, b, r) 中局部最大点。
4.3 霍夫变换的其他应用
除了检测出直线、圆等几何体,此算法进一步还能做一些其他事,因为最近几年没什么进展了,就不细研究了。
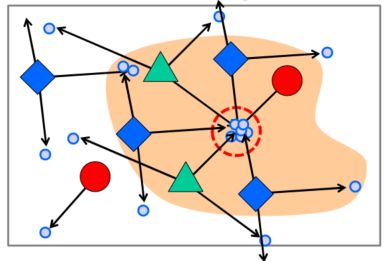
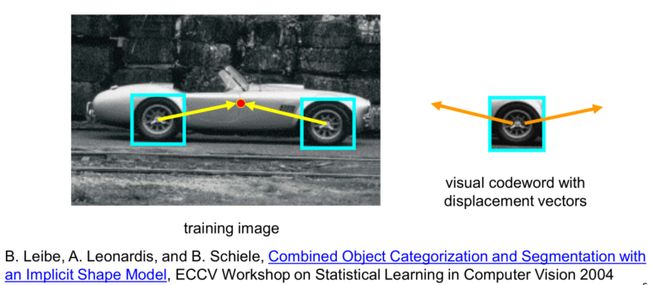
案例:通过检测一些大物体的局部组件相对大物体的位置关系,通过方向投票机制,去锁定图像中某大物体的中心位置。
5 总结
本专题介绍了图像拟合的一些经典计算机视觉方法,虽然这些方法在深度学习时代竞争力已不大,但是其经久考验的算法思想还是很值得学习的。通过本专题整理,收获主要如下:
- 霍夫变换思想,真的让我震惊了,感觉可以和DL技术相结合。
- 投票机制。
- 图像噪声对各种算法的影响,以及应对措施,这方面非常麻烦,效果也要特定问题特定分析,让我更加感受到深度学习技术的潜在威力。