Spark 3.0 - 13.ML Kmeans 聚类理论与实战

目录

一.引言

二.Kmeans 理论

1.算法基础

2.算法示例

三.K-means 实战

1.数据准备

2.构建 K-means 模型

3.模型评估

4.获取聚类中心

四.总结

---

一.引言

聚类是一种数据挖掘领域中常见的无监督学习算法，用于挖掘数据之间的潜在属性。ML 中聚类的算法目前有4种，其中最常用的就是 K-means 算法，在多个领域中应用较为广泛。除此之外，还有高斯混合聚类、快速迭代聚类与隐狄利克雷聚类，后面也会介绍其中的这几个聚类算法。

Tips：

这里同学们要和前面常提到的分类区分开关系。一般来说分类是指有监督的学习，其样本是有标记的，类别是已知的；聚类是指无监督学习，样本没有标记和 Labels，我们只是通过学习一套衡量标准，然后依据无监督学习到的标准将样本聚为 K 类。

二.Kmeans 理论

1.算法基础

K-means 是最为经典的基于划分的聚类方法，是十大经典数据挖掘算法之一。其算法的基本思想是：以空间中 K 个点作为中心进行聚类，对最靠近它们的对象进行归类。通过迭代的方法，逐次更新各个聚类中心的值，直至得到最好的聚类效果。

一般来说，K-means 通过欧氏距离衡量两个样本之间的距离：

其中 x、y 为 K 维样本，这里 K 与要聚类的 K 非同一个 K，需要区分。最后迭代生成多个聚类中心，再新增样本时，判断其与哪个聚类中心的欧氏距离最短，以最短的聚类中心对应类作为该样本的无监督样本类。

2.算法示例

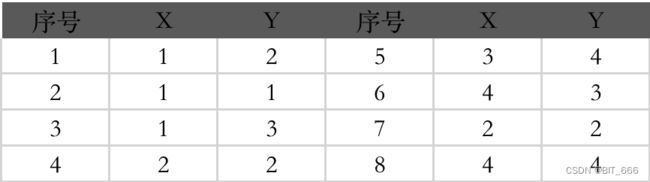
假设当前存在8个二维样本，要将全部样本生成 K=2 类。

A.随机选定两个初始中心点

假设选择序号 2、5 对应的数据作为初始点，分别寻找与其距离近的样本作为聚类数据集。

序号2：[1,2,3,4,7]

序号5：[5,6,8]

B.更新聚类中心

得到新的聚类中心 (1.4,2) 与 (3.666,3.666)

C.重新构造聚类数据集

基于新的数据中心重新选定聚类数据集，如此循环，当中心点数据不再更改或者移动距离相当小时，可以认为聚类达到最优聚类。对于 K-means 而言，如何选择 k(簇个数) 和中心点的选取是影响效果的两个常见的问题，下图显示了随机初始化2个中心点后，不断重复并更新聚类中心，最后达到收敛条件获得聚类中心的过程。

 

三.K-means 实战

1.数据准备

0 1:0.0 2:0.0 3:0.0
1 1:0.1 2:0.1 3:0.1
2 1:0.2 2:0.2 3:0.2
3 1:9.0 2:9.0 3:9.0
4 1:9.1 2:9.1 3:9.1
5 1:9.2 2:9.2 3:9.2

这里简单准备一些3维度数据，同学们也可以使用自己的数据进行聚类测试。

    val spark = SparkSession
      .builder      //创建spark会话
      .master("local")  //设置本地模式
      .appName("K-means")  //设置名称
      .getOrCreate()   //创建会话变量

    // 读取数据
    val dataset = spark.read.format("libsvm").load("./sample_kmeans_data.txt")

 

2.构建 K-means 模型

    // 训练模型，设置参数，载入训练集数据正式训练模型
    val kmeans = new KMeans().setK(3).setSeed(1L)
    val model = kmeans.fit(dataset)

下面简单看下模型参数：

distanceMeasure: 距离度量。支持的选项：“欧氏” - euclidean 和“余弦” - cosine(default: euclidean)
featuresCol: 要素列名称（默认值：要素） (default: features)
initMode: 初始化算法。支持的选项：“random”和“k-means||” (default: k-means||)
initSteps: k-means||初始化模式的步骤数。必须大于0。 (default: 2)
k: 要创建的群集数。必须大于1。 (default: 2, current: 3)
maxIter: 最大迭代次数（>=0） (default: 20)
predictionCol: 预测列名称 (default: prediction)
seed: 随机种子 (default: -1689246527, current: 1)
tol: 迭代算法的收敛公差（>=0） (default: 1.0E-4)
weightCol: 权重列名称。如果未设置或为空，则将所有实例权重视为1.0 (undefined)

这里将数据分为 3 类，通过 setK 方法即可指定最终的聚类中心簇的个数，这是最简单的模型初始化方法。maxIter 和 tol 规定了两种退出训练的方法，一种是迭代达到 maxIter 另一种是迭代算法的收敛公差小于 tol 的值。除此之外，weightCol 可以对指定维度的数据加权，这样计算计算距离时加权样本将更多的影响距离的计算。

除了常规的欧式距离外，这里也可以基于余弦距离进行计算：

夹角余弦值越大代表二者越接近，反之二者距离越大。

3.模型评估

    // 使用测试集作预测
    val predictions = model.transform(dataset)

    // 使用轮廓分评估模型
    val evaluator = new ClusteringEvaluator()

    val silhouette = evaluator.evaluate(predictions)
    println(s"Silhouette with squared euclidean distance = $silhouette")

这里直接使用训练数据预测其无监督分类簇。ClusteringEvaluator 用于计算轮廓分数，它测量一个簇中的每个点与相邻簇中点的接近程度，从而帮助判断簇是否紧凑且间隔良好。时间复杂度 O(tknm)，空间复杂度 O(m(n+k))。其中 t 为迭代次数、k 为簇的数目、n 为样本点数、m 为样本点维度。

Silhouette with squared euclidean distance = 0.6248737134600261

轮廓是验证集群内一致性的一种度量。它的范围在 1 和 -1 之间，其中接近 1 的值意味着集群中的点靠近同一集群中的其他点，而远离其他集群的点。

4.获取聚类中心

    // 展示结果
    println("Cluster Centers: ")
    model.clusterCenters.foreach(println)

    spark.stop()

Cluster Centers: 
[9.1,9.1,9.1]
[0.05,0.05,0.05]
[0.2,0.2,0.2]

基于上述聚类中心，再来新的样本即可通过计算与各个中心点的欧式距离判断该样本距离哪个簇中心更近，从而将簇中心对应的样本类型作为当前样本的类型。

四.总结

K-means 虽然是最基础最简单的无监督聚类算法，但是其在大规模数据状态下对数据的聚类分簇效果很好，得到的分类簇信息也可以用于后续的特征工程，非常好用，大家可以尝试。