基于LSTM的故障诊断
0 引言
很少基于pytorch框架的故障诊断模型搭建,也对自己前期的实验做个总结,欢迎讨论。
框架:pytorch
硬件:Intel(R) Core(TM) i5-10500H CPU @ 2.50GHz 2.50 GHz
1650
1 数据集
数据集:凯斯西储大学(CWRU)滚动轴承数据。
2 实验对象
2.1 数据集说明
故障轴承以激光蚀刻加工制作,人为在轴承上蚀刻单点缺陷模拟轴承的故障,缺陷点的大小设置(7,14,21,28)mils 四种类型。轴承振动数据使用加速度传感器进行信号采集,采样频率为 12000Point/S(12kHz)及 48000point/S(48kHz)。
具体说明可到官网查看。
本实验采用驱动端的轴承振动数据,采样频率选择 12kHz。
2.2 故障标签
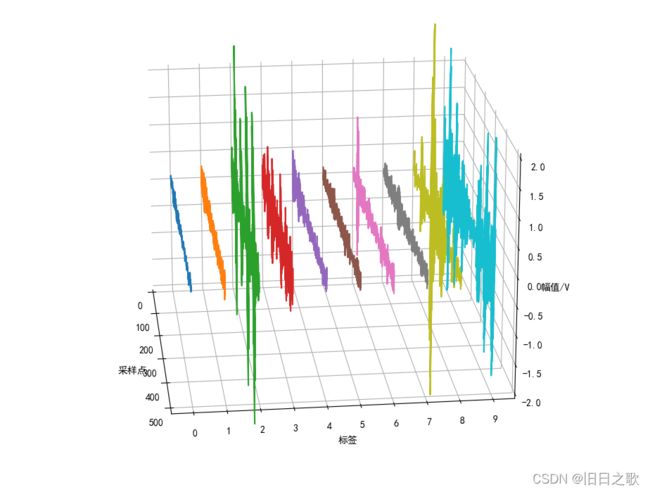
2.3 数据对比
标签太多不好对比 ,感觉用matlab画这个要更直观和方便些,数据提取嫌麻烦就没搞了。
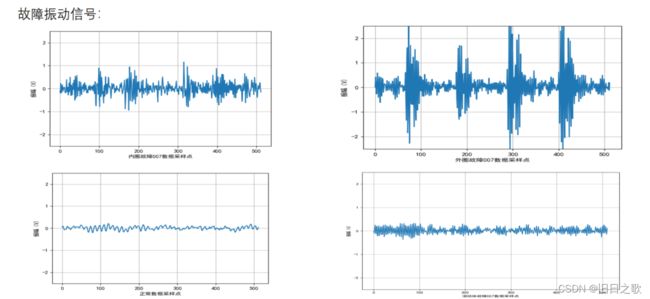
一维查看:
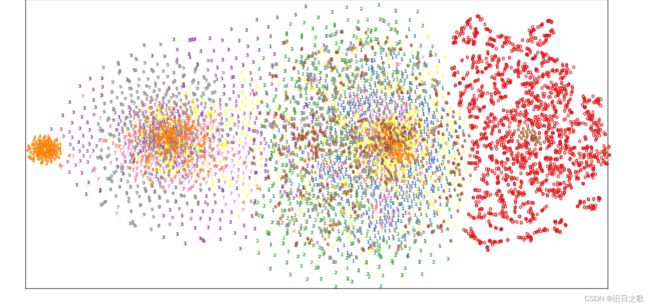
t-sne训练集可视化:
data_sne=data_valid_last #[3385x512] list_target对应的标签
tsne = TSNE(n_components=2,init='pca',learning_rate=200)
X_tsne=tsne.fit_transform(data_sne)
x_min,x_max=X_tsne.min(0),X_tsne.max(0)
X_norm = (X_tsne - x_min) / (x_max - x_min) # 归一化
plt.figure(figsize=(12, 12))
print(X_norm.shape)
for i in range(X_norm.shape[0]):
plt.text(X_norm[i, 0], X_norm[i, 1], str(list_target[i]), color=plt.cm.Set1(list_target[i]),
fontdict={'weight': 'bold', 'size': 6})
plt.xticks([])
plt.yticks([])
time_end=time.time()
time_c=time_end-time_start
print("time cost:{}min{}s".format(int(time_c/60),int(time_c%60)))
plt.show()3 数据处理
3.1 数据预处理
def data_load(path, data_name, cut_num, label):
"""
:param path: 数据地址
:param data_name: 数据名称
:param cut_num: 每份样本数量,cut_length
:param label: 数据标签
:return: data_cut, label_cut
"""
name_str=str(data_name)
data=loadmat(path+name_str+'.mat') #数据加载为字典格式,data为字典
if data_name<100: #如X097_DE_time,数据提取格式
data_name='0'+str(data_name)
else:
data_name=str(data_name)
#原始数据提取
org_DE=data['X'+data_name+'_DE_time']
org_FE=data['X'+data_name+'_FE_time']
# 数据归一化
# 归一化DE
scaler = MinMaxScaler()
list_DE_n = scaler.fit_transform(org_DE)
list_FE_n =scaler.fit_transform(org_FE) #风扇端数据
list_DE = []
for de in list_DE_n:
list_DE.append(de[0])
list_FE = []
for fe in list_FE_n:
list_FE.append(fe[0])
list_r = []
# 分割数据
data_cut = []
label_cut = []
for i in range(0, int(len(list_DE_n) / cut_num)): #分成i个
data_cut.append(list_DE[i * cut_num: (i + 1) * cut_num])
label_cut.append(label)
return data_cut, label_cutdata_97,label_97=data_load('data/Normal Baseline Data/',97,cut_length,0)
data_98,label_98=data_load('data/Normal Baseline Data/',98,cut_length,0)
data_99,label_99=data_load('data/Normal Baseline Data/',99,cut_length,0)
data_100,label_100=data_load('data/Normal Baseline Data/',100,cut_length,0)
# print(np.asarray(data_97,dtype = 'float').shape)
data_normal = data_97 + data_98 + data_99 + data_100
label_normal = label_97 + label_98 + label_99 +label_100
print("处理后正常样本shape:",np.asarray(data_normal,dtype = 'float').shape)
print("label数:",len(label_normal))
notes:其中正常样本是其他单个样本的三倍。
3.2 数据加载、划分及处理
batch_size=128 # 批量大小
train_data_loader=DataLoader(data_train_last,batch_size,drop_last=True)
train_label_loader=DataLoader(data_train_label,batch_size,drop_last=True)
valid_label_loader=DataLoader(valid_label,batch_size,drop_last=True)
valid_data_loader=DataLoader(data_valid_last,batch_size,drop_last=True)3.3 数据打包
4 模型构建
超参数设置:
epoch可以设置的大一些,我平常都是500,写这篇文章为了节约时间才设置的150,在后面正确率还可以浅浅的上升。
loss_n=nn.CrossEntropyLoss()
optimizer=torch.optim.Adam(params=LsTm.parameters(),lr=0.001,betas=(0.9,0.999),eps=1e-08,weight_decay=1e-4)
epoch=1504.1 LSTM
输入大小为:[128,512,1]
class mylstm(nn.Module):
def __init__(self):
super(mylstm, self).__init__()
self.modle1 = nn.LSTM(input_size=1,hidden_size=16,num_layers=2, batch_first=True, dropout=0.2)
self.modle2=nn.Sequential (
nn.Flatten(),
nn.Linear(16*512,256),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(256,10)
)
def forward(self, x):
h_0 = torch.randn(2, 128,16)
c_0 = torch.randn(2,128, 16)
h_0=h_0.cuda()
c_0=c_0.cuda()
x = x.to(torch.float32)
x,(h_0,c_0)=self.modle1(x,(h_0,c_0))
#x=x[:,-1,:]
x=self.modle2(x)
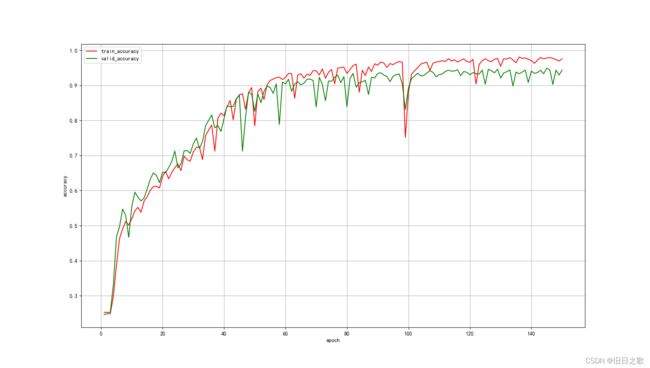
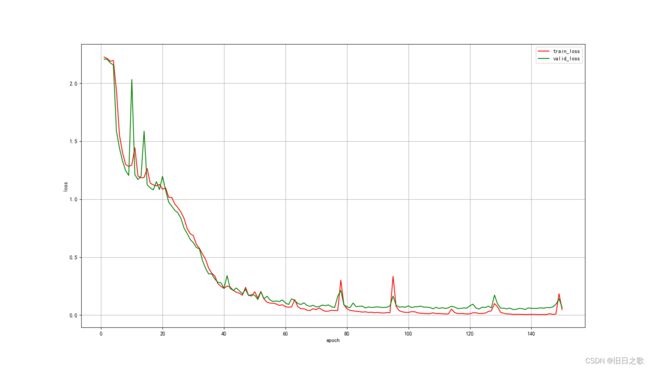
return x4.1.1 结果
train_last_10_epoch_avg_accuracy:0.9739
valid_last_10_epoch_avg_accuracy:0.9356
time cost:8min48s
4.2 LSTM-1DCNN
后面就接了个一维池化层。
class mylstm(nn.Module):
def __init__(self):
super(mylstm, self).__init__()
self.modle1 = nn.LSTM(input_size=1,hidden_size=16,num_layers=2, batch_first=True, dropout=0.2)
self.modle2=nn.Sequential (
nn.AvgPool1d(16),
nn.Flatten(),
nn.Linear(512,256),
nn.ReLU(),
# nn.Dropout(0.2),
nn.Linear(256, 64),
nn.ReLU(),
nn.Linear(64,10)
)
def forward(self, x):
h_0 = torch.randn(2,batch_size,16)
c_0 = torch.randn(2,batch_size, 16)
h_0=h_0.cuda()
c_0=c_0.cuda()
x = x.to(torch.float32)
x,(h_0,c_0)=self.modle1(x,(h_0,c_0))
#print(x.shape)
#x=x[:,-1,:]
x=self.modle2(x)
return x 4.2.1 结果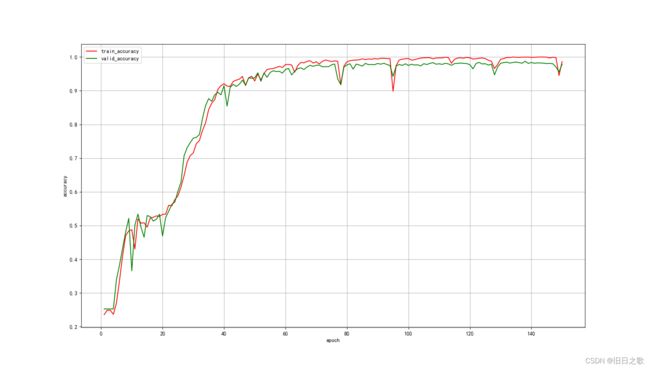
train_last_10_epoch_avg_accuracy:0.9937
valid_last_10_epoch_avg_accuracy:0.9779
time cost:8min36s
5 总结
过拟合和稳定性还有很大的提升。
dropout要慎重,极大可能丢弃掉一些重要的神经元,导致损失值突变。
加入注意力机制后几乎没啥改变。
LSTM后面可以接二维卷积或者一维卷积用大的卷积核,提高感受视野,效果有提升。
怎么花怎么来吧。