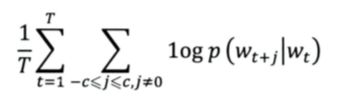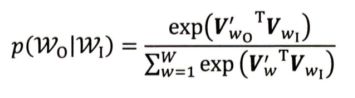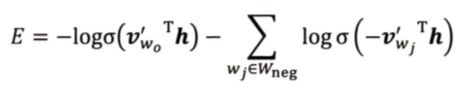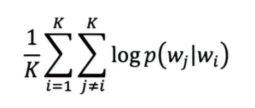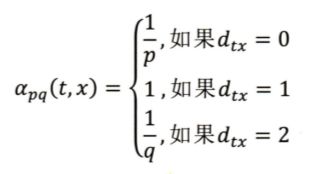推荐系统（Recommender System）笔记 02：Embedding

什么是 Embedding？

我们在之前介绍模型时，不知一次提到了 Embedding 操作，彼时我们主要将它当作 “把稀疏向量转换为稠密向量” 的操作。但事实上，Embedding 操作的作用远不止于此。Embedding 是用一个低维稠密的向量 “表示” 某个对象，该向量能够表达相应对象的某些特征，同时，向量之间的距离可以直接用以度量对象之间的相似性

词向量

熟悉 NLP 的朋友对于 Embedding 这个词一定不陌生，word2vec 就是 Word Embedding 的方法之一。 所谓的 Word Embedding 就是将「不可计算」「非结构化」的词转化为「可计算」「结构化」的向量。这一步解决的是 ”将现实问题转化为数学问题“，是人工智能 NLP 非常关键的一步。

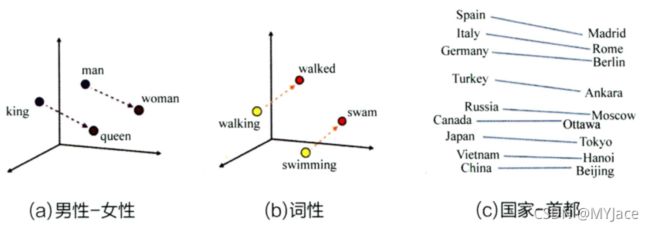
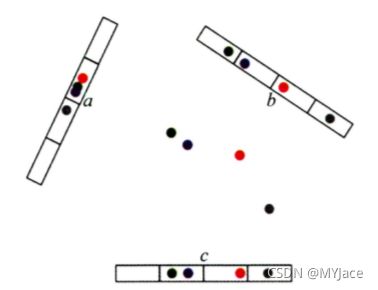
上图 (a) 中是使用了 word2vec 编码的具有 “性别” 特征的 Embedding 向量在 Embedding 向量空间内的位置。可以看到，Embedding (man) 到 Embedding (woman) 的记录向量和从 king 到 queen 的距离向量基本一致，这就表明 Embedding 向量之间的计算甚至可以包含词之间的语义关系。同样，图 (b) 则体现出这一特点。

除此以外，Embedding 技术在语料库充足的情况下甚至可以挖掘出符合通识概念的常识。比如 © 中城市 - 国家向量基本全部一致。如此一来，我们可以得到一个结论：Embedding 就是从其向量空间维度来表达物品，并揭示物品之间关系的方法。

Embedding 对于深度学习的重要性

Embedding 技术对于深度学习有着重要影响的原因主要有三：

1. 推荐场景中如果使用 one-hot 编码对 ID、类别型特征进行编码，会产生大量稀疏向量。而深度学习不利于处理这样的稀疏向量。因此选择使用 Embedding 将这些高维稀疏向量转换为低维稠密向量
2. Embedding 本身就是能够表达更多信息的重要的特征向量。 因此，我们往往会选择将 Embedding 向量与其他推荐系统特征连接后，一同作为模型训练的数据
3. Embedding 对物品、用户的相似度计算是常用的推荐系统的召回技术。 换言之，非常适合对于海量候选对象进行 “初筛”

Word2vec

我们之前已经提到过，Word2vec 是 NLP 中一种常用的 Embedding 方法。Word2vec (Word to vector) 是一个生成对 “词” 的向量表达的模型。这个模型的训练需要一个由大量句子构成的语料库

我们都清楚，一个长度为 T 的句子由众多单词组成 (w₁, w₂, … , w_T)。而每个词都与其最相邻的词关系最亲密，据此，我们可以得到 Word2vec 的 2 种模型：

• CBOW：每个词由相邻的词决定
• Skip-gram：每个词都决定了相邻的词

根据上述的定义和图解，我们能够很轻松地得出这两个模型如下所示的结构图：

可以看到：

• 左侧为 CBOW 模型，它的输入是 w_t 周边的词，预测的输出是 w_t
• 右侧为 Skip-gram 模型，它的输入是 w_t，预测的输出则是其周围的词

我们接下来以 skip-gram 为例子来了解模型的训练过程。（因为从经验上来说，skip-gram 的效果比 CBOW 更理想）

训练过程

首先，要从语料库中获取训练数据集，即一系列的句子。 具体做法是用一个 size 为 2c + 1 （目标词前后各选 c 个词）的 sliding window，从左向右滑动，以此从语料库中生成了一系列句子。

接下来，需要确定优化目标。 因为我们已经知道，每个词 w_t 都决定了相邻的词 w_t+j，所以基于极大似然估计 (Maximum Likelihood) 是很合理的。即希望所有样本的条件概率 p(w_t+j|w_t) 之积是最大的，为了简化计算，将积的形式转换为和的形式，可以使用对数方法。 因此，我们可以得到一个如下所示的目标函数：

作为一个多分类问题，我们可以选择使用 softmax 来定义 p(w_t+j|w_t)。作为一种 Embedding 方法，word2vec 的目标在于能使用一个向量 v_t 来表示单词 w_t，同时向量之间的内积距离 v_i^Tv_j 可以表示两个词之间语义的接近程度。因此，我们可以得出 p(w_t+j|w_t) 的公式如下所示：

这个式子中用 w_I 表示输入词，即 w_t；w_O 表示输出词，即 w_t+j。而这里的 V_wI 和 V_wO 就是词的输入和输出的向量表达。这里就需要结合 word2vec 的网络结构来理解什么是向量表达：

在这个模型中，输入向量表达就是输入层 (Input Layer) 到隐藏层 (Hidden Layer) 的权值矩阵 W_VxN，而输出向量表达就是从隐藏层 (Hidden Layer) 到输出层 (Output Layer) 的权值矩阵 W’_NxV。

我们来具体地看一下，当我们已经获得输入向量矩阵 W_VxN 之后，该矩阵中地每一行对应地权重向量就是所谓的 “词向量”。因此，这个矩阵自然就变为 word2vec 的查找表 (lookup table)。

上图是一个具体的例子，假设我们的输入是 10000 个词组成的 one-hot 向量（换言之，我们的语料库中共有 10000 个单词，如果当前输入的这个词是 orange，这个词在所有词中是第 6257 个，那么，此时的输入向量在第 6257 位为 1，其余位全部为 0，是一个极为稀疏的向量）。隐藏层的维度为 300，如此一来输入层到隐藏层的权值矩阵就是 10000 x 300 维，这个时候，矩阵中的每一行向量就是对应一个词的 Embedding 向量

*这里需要注意一下，上图中的矩阵是同一个矩阵，我们只是改变了看待它的角度，从原本的纵向角度变为横向角度来看而已，并不是生成一个全新的矩阵

“负采样”（Negative Sampling）

上述的 word2vec 常规训练过程会有一个缺陷。还是用上面的那个例子，如果语料库中有 10000 个单词，那么输出层神经元也会有 10000 个，每次进行迭代更新隐藏层到输出层的权值矩阵时，就需要计算所有 10000 个单词的预测误差 (Prediction Error)，这样的计算量是无比巨大的。

因此会采用 “负采样” 的方法。此时就不需要再计算字典中所有词的预测误差，只需要对采样出的几个负样本计算预测误差即可。 此时 word2vec 就从原本的多分类问题近似转换为二分类问题。

**其中 V’_wO 是输出词向量（正样本），h 是隐藏层向量，W_neg 是负样本集合，V’_wj 是负样本词向量。**一般来说负样本集合的规模 k 在小数据集中取 2~5，在大数据集中取 5 ~ 20，所以计算量会大大降低。

Item2vec - Word2vec 在推荐系统中的推广

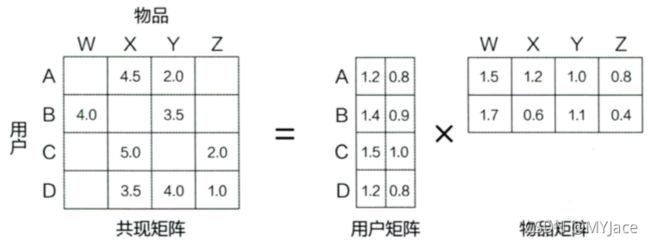
我们在 Word2vec 中已经成功对词序列中的词进行了 Embedding，那么对于用户浏览序列中的一件商品、一部电影应该也能进行 Embedding，这就是 Item2vec 的基本思想。我们这里稍微回顾一下之前介绍过的矩阵分解 (MF)，这个方法会将贡献矩阵分解为用户矩阵 (User Matrix) 和对象矩阵 (Item Matrix)：

此时在这两个矩阵中的用户隐向量以及对象隐向量实际上就是用户 Embedding 向量以及对象 Embedding 向量。

随着 Embedding 方法的发展，对象 Embedding 的生成有着更多的选择，而对于用户 Embedding 来说则可以通过历史浏览的对象的 Embedding 向量平均或者聚类得到。只要有了用户 Embedding 以及对象 Embedding 就能计算两者的相似性，这是在推荐系统中进行召回（获得候选集）以及对最终推荐列表进行排序的重要手段。

现在具体来看 Item2vec。和 Word2vec 一样，我们需要一个 “序列”，Word2vec 使用的是 “句子”，而在 Item2vec 中，我们使用的是 “对象序列”，即特定用户的浏览、购买等行为产生的历史序列。假如我们有一个长度为 K 的用户历史记录：w₁, w₂, w₃, …, w_K。和 Word2vec 一样，我们仍选择最大似然作为优化目标：

与 Word2vec 不同的地方在于，这里我们摒弃了 “时间窗” 概念，我们不再认为每个词只和前后 c 个相邻词相关（时间窗为 2c + 1），而是认为序列中任意两个对象都相关，因此这里不再只是时间窗内物品对数概率之和，而是两两对数概率之和。

在确定优化目标之后，后续的训练流程和 Word2vec 基本一致，最终对象的查找表就对应 Word2vec 中的词查找表。此时在这个对象查找表中的每一行就对应对象的 Embedding 向量。

广义上的 Item2vec 指代的是任何能生成物品向量的方法。比如典型的双塔模型：

我们将广告侧的模型结构称作 “物品塔”，这部分实现的就是对物品（对象）的 Embedding 过程。该侧模型接收物品相关的特征向量。这里的特征向量不再是用户行为序列生成的 one-hot 特征向量，而是包含更多信息的、全面的物品特征向量。该特征向量经过物品塔内的多层神经网络变为一个多维稠密向量，也就是物品的 Embedding 向量。

广义的 Item2vec 就是将对象/物品向量化的方法，可以利用不同的深度学习模型对对象/物品特征进行向量化。但是 Item2vec 也存在其局限性，因为只能序列性数据，所以对于现今大量存在的网络化数据显得力不从心。

Graph Embedding

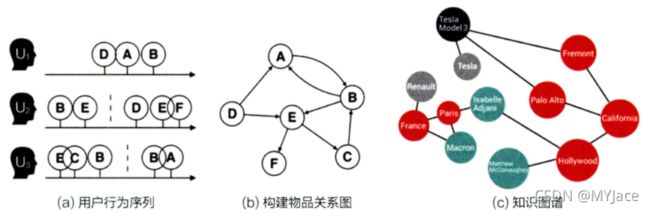
Grapgh Embedding 就是应对网络化数据，引入了更多结构信息的图嵌入技术。所谓的网络化数据，数据之间往往会具备 “图” 的结构，最典型的就是用户行为序列生成的物品关系图，以及由实体 (Entity) 和属性 (Attribute) 生成的知识图谱 (Knowledge Map)：

Graph Embedding 是一种对图中节点 (Node) 进行 Embedding 编码的方法。最终生成的 Embedding 向量一般包含图的结构信息和附近节点的局部相似性信息。

DeepWalk

DeepWalk 是最基础的 Graph Embedding 方法。它的核心思想是在由物品组成的网络上进行随机游走，以此产生大量物品序列，然后用这些序列作为训练样本输入给 Word2vec 进行训练，得到物品的 Embedding。

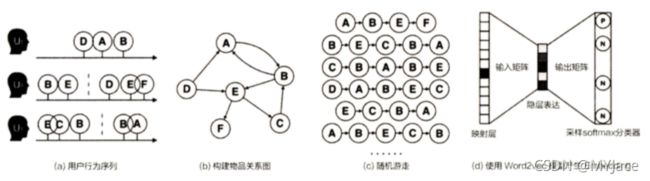
上面的流图就是 DeepWalk 的整个流程：

a). 获取用户的原始序列

b). 使用原始序列构建物品关系图。需要注意的是这张图中的边都是有向边，因为序列表示了 “时序” 特征，因此物品之间也应当体现出这种顺序，比如 U₁ 先买了 A 再买了 B，所以就出现了 A → B，这条边。如果后续多次出现同样的有向边，那么这条边的权值就会增大

c). 随机选择初始点，通过随机游走重新产生物品序列

d). 将这些序列输入给 Word2vec，生成最终的物品 Embedding 向量

在整个随机游走的过程中，我们最需要注意的就是 “如何确定下一步该走到哪个点”。我们可以形式化地将其定义为：到达节点 v_i 之后，下一步遍历相邻点 v_j 的概率。我们之前已经说过，每条有向边有权值，因此可以将这种概率定义为：

在这个式子中，ε 是物品关系图中所有边的集合 ， N₊(V_i) 是节点 V_i 所有的出边集合 ， M_ij 是节点 V_i 到节点巧边的权重。所以，实际上就是根据每一条出边的权值比重来决定走哪个方向，权值越高，走的概率越大。

如果都是无向边，那么此时 N₊(V_i) 是节点 V_i 所有的边集合，且此时 M_ij 为常数 1

Node2vec

同质性 (Homophily) 和结构性 (Structual Equivalence)

Node2vec 主要调整了随机游走的权重机制，使得 Graph Embedding 的结果更能体现网络的结构性 (Structual Equivalence) 以及同质性 (Homophily)：

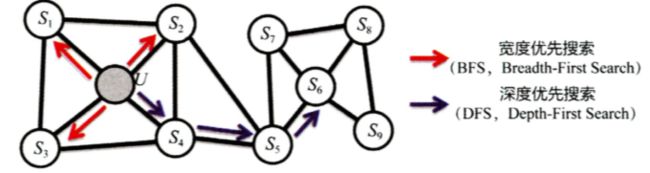
• 同质性 (Homophily)：相邻节点的 Embedding 应当尽量相似。 比如下图中节点 U 与其相邻的 S₁, S₂, S₃, S₄ 的 Embedding 表达应当尽量相似
• 结构性 (Structual Equivalence)：结构上相似的节点，Embedding 应当尽量相似。 比如下图中节点 U 和节点 S₆ 都是各自局域网络的中心点，因此它们在结构上具有相似性，所以它们的 Embedding 应该尽量相似

为了使得 Graph Embeeding 的结果更能表达网络的 结构性 (Structual Equivalence)，应当使随机游走的过程更类似 BFS。这似乎和我们的直觉理解相悖：因为 BFS 更倾向于优先游走到当前节点的相邻节点上，因此会将更多的同质性 (Homophily) 信息包含到生成序列之中，而不是结构性 (Structual Equivalence)。但事实并非如此：

因为 BFS 搜索的范围往往在当前节点（比如节点 U）的邻域。而在 Node2vec 中，是存在返回概率的，所以即便从 U 走到了 S₁，但下一步仍有很高的概率从 S₁ 走回 U，此时 BFS 生成的序列显示出来的结果就是在 U 和其附近节点之间来回震荡，这实际上就是对 U 周围的网络结构进行了局部扫描，得到了当前这一局域网络的结构信息。

再举一个例子，上图中，U 是局部网络的中心点， S₉ 是边缘节点。那么在该网络中进行多次 BFS 随机游走时， 节点 U 必定会被多次遍历，且会与 S₁ - S₄ 等节点发生联系，而边缘节点 S₉ 无论从遍历的次数还是相邻点的数量都不及 U，因此两者的 Embedding 会相差巨大。此时根据这样的 Embedding 就能直观辨别出当前节点是 “局部中心点” 还是 “边缘点”，这其实就是因为包含了更多的结构信息。

而为了表达 同质性 (Homophily)，则应当使用 DFS。同样，我们之前已经说过，根据直觉来说似乎 BFS 更适合表达同质性，但是事实依旧与我们的 “常识” 相悖。

这是因为我们对于同质性 (Homophily) 的理解收到了局限，这里的同质性 (Homophily) 指的是一个社区、集群、聚类的同质性。因此需要借助 DFS 进行更广范围的搜索，如果仍使用 BFS 的局部范围探索，会很首先。所以 DFS 相当于对网络进行了以此宏观扫描 (Macroscope Scan)，从宏观视角，发现更大的社区、集群、聚类中的同质性 (Homophily)

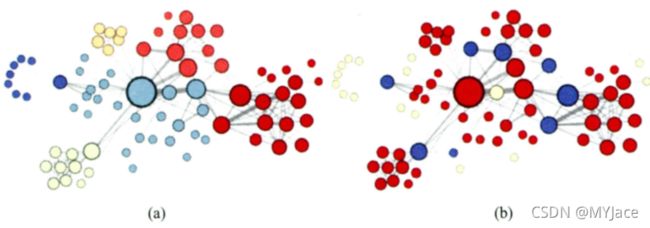
可以用实验的方式去验证这种结论：

上图是在网络中进行 DFS 搜索的结果，下图是 BFS 结果。图中颜色相近的节点表示 Embedding 相似性更强。 可以看到，上图中各聚类的内部节点相似，这是 “同质性” 的体现；而下图中结构类似节点的 Embedding 更相似，体现了 “结构性”。

最后我们结合具体的推荐场景来总结一下：结构性 (Structual Equivalence) 关注特定的节点在网络中的位置，比如是中心点还是边缘点，不关心节点本身的特有属性。类似每个品类的热门商品、热销商品，虽然商品类型不同，但是都是 “热销”。同质性 (Homophily) 相反，更多关注内容本身的相似性，所以同品类、同商铺等内容更容易表现同质性。

切换 BFS 和 DFS 倾向性

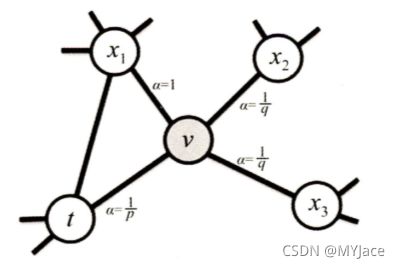
在 Node2vec 中，主要通过节点间的跳转概率来控制 BFS 和 DFS 的倾向性。

上图中显示了从点 t 跳转到点 v 以及从点 v 跳转到周围点的概率。从节点 v 跳转到下一个节点 x 的概率为：

π_vx = α_pq(t, x) * w_v,x

其中 w_v,x 为边 vx 的权重，α_pq(t, x) 的定义如下所示：

这里的 d_tx 就是节点 t 到节点 x 的距离，参数 p 和 q 共同控制着随机游走的倾向性：

• 参数 p 就是返回参数 (return parameter)，p 越小，随机游走回到节点 t 的概率越大，Node2vec 就更偏向于 BFS，换言之更注重网络的结构性 (Structual Equivalence)
• 参数 q 就是进出参数 (in-out parameter)，q 越小，随机游走更可能走向远处，Node2vec 更偏向于 DFS，注重表达网络的同质性 (Homophily)

同质性相同的物品很可能是同品类、同属性或者经常被一起购买的商品，而结构性相同的商品则是各品类的爆款、热销或最佳凑单商品等具有类似趋势和结构性属性的物品。

EGES - 综合性 Graph Embedding

EGES (Enhanced Graph Embedding with Side Information) 的基本思想是在 DeepWalk 生成 Graph Embedding 的基础上引进补充信息。这里引入补充信息主要是为了应对 “冷启动” 问题。

我们在使用用户的行为序列去生成物品 Embedding 会存在一个问题。那就是当有全新的物品加入到内容池，这些新物品由于是新品，可能初期用户很少，用户行为自然就不会多，此时就很难在用户的行为序列中发现这些新物品，因此无法训练出合适的模型去推荐这些新物品。这就是所谓的 “冷启动” 问题

所以，为 “冷启动” 商品赋予一个合适的初始 Embedding 就显得很重要，因此，对于这些没有历史行为记录的商品，使用补充信息去赋予合理的初始 Embedding 就显得很有必要。

在此之前，我们使用用户的行为序列生成了物品关系图，但我们也可以选择基于内容生成知识图谱。 比如我们利用 “相同类别”，“相同属性” 等性质构建物品之间的边。而基于知识图谱生成的物品向量也叫做补充信息 Embedding 向量。因此根据补充信息的不同，同一个物品可能会有多个补充信息 Embedding 向量。

当然，我们最终希望用一个 Embedding 向量就能够表示一个物品，因此，如果一个物品有多个 Embedding 向量，自然是需要合并的。最简单的合并方式就是使用平均，在网络中加入一个平均池化层就能够实现。但是为了避免平均池化导致的有效信息丢失，可以类比 DIN 中的注意力机制，为每个 Embedding 赋予不同的权值

在上图所示的网络结构中，为每个类别特征对应的 Embedding 分别赋予了权值 α₁, α₂, …, α_n 。图中的隐表达层 (Hidden Representation Layer) 所做的工作就是对所有的 Embedding 加权求平均，然后将结果输出给 softmax 层。整个模型通过梯度反向传播进行调参，得到每个 Embedding 的权值 α_i

阿里的 EGES 中，每个 Embedding 对应的权值选择了 e^αj 而不是 α_j。这是因为可以避免 0 权值的出现，同时 e^αj 在梯度下降中有比较好的数学性质

因此，我们可以说 EGES 的主要特征在于它提出了一种在工程上融合多种 Embedding 的方法，降低了某类信息确实造成的 “冷启动” 问题

Embedding 与 DL 的结合

在推荐系统中，Embedding 需要作为一个部件与深度学习网络的其他部分协同完成推荐工作。Embedding 在 DL 中主要有以下三种用途：

1. 作为 Embedding 层，将高维的稀疏输入向量转换为低维的稠密特征向量
2. 作为预训练的 Embedding 特征向量，与其他特征的向量拼接后一同输入深度学习网络进行训练
3. 通过计算用户与物品的 Embedding 向量相似度，Embedding 可以直接作为召回的策略

Embedding 层

Embedding 层我们在之前介绍各类模型时已经有所接触，其使命在于将高维稀疏特征向量转换为低维稠密特征向量，其位置一般位于输入层 (Input Layer) 和全连接层 (Fully Connect Layer) 之间。

比如我们之前介绍过的 Deep Crossing，FNN，Wide&Deep 都具有 Embedding 层：

可以看到，这里所有 Embedding 接受的输入都是类别型特征的 one-hot 向量。根据 Embedding 层的任务，我们实际上可以将其看作是一个从高维向量向低维向量的直接映射。所以，我们可以选择使用矩阵来表示 Embedding 层：

因此对于 Embedding 层的训练和调参，实质上就是求解这个 m x n 维的权值矩阵的过程。这里的 m 就是输入 one-hot 矩阵的维度，n 就是转换后的稠密向量的维度。此时，如果输入就是 one-hot 向量，则该权值矩阵中对应的列向量就是相应维度 one-hot 特征的 Embedding 向量。

但是我们之前说过，由于 Embedding 层的输入往往是高维的稀疏矩阵，这会导致在本层需要训练的参数量极大，因此会拖慢模型的训练速度以及收敛速度。

Embedding 的预训练方法

为了应对直接向模型加入 Embedding 层带来的问题。现在会选择独立于深度学习网络，单独训练 Embedding。使用时，直接将稀疏向量输入给已训练好的 Embedding，把得到稠密向量结合其他特征向量直接输入给神经网络进行训练。在之前介绍的 FNN 模型实际上已经运用了这种思想（将 FM 模型训练得到的各特征隐向量作为 Embedding 的初始权重）。

值得注意的是，在这里我们仅仅将 Embedding 层的初始权值进行设定，也就是说，随着训练的进行，这部分的权值是会不断更新的，我们为其赋予的这批初始权值是为了加快收敛的速度。当然，我们也可以选择 “固定 Embedding 层的权值，只更新上层网络的权重”

Embedding 的本质实际上就是 “从高维向低维的映射”。而实现这种映射不一定需要借助神经网络，也可以使用其他方式，比如之前介绍的 GBDT + LR 模型，它的 GBDT 部分实际上就是预训练 Embedding，然后将 Embedding 输入给单层神经网络的 LR 模型进行 CTR 预测。

使用 Embedding 预训练的好处在于独立的训练过程提高了训练的灵活性。这很好理解，因为用户的兴趣以及商品的信息很少会在短期的一两天内发生翻天覆地的变化，因此我们可以适当降低 Embedding 训练的频率，比如以周为单位。而上层的神经网络为了尽可能多抓取最新的数据特征，需要更高的训练频率，比如以天为单位。

Embedding 作为系统召回的方法

得益于 Embedding 现在可以将各类补充信息融入其中，它的表达能力在不断增强，这就使得直接利用 Embedding 生成推荐列表具备了可行性。

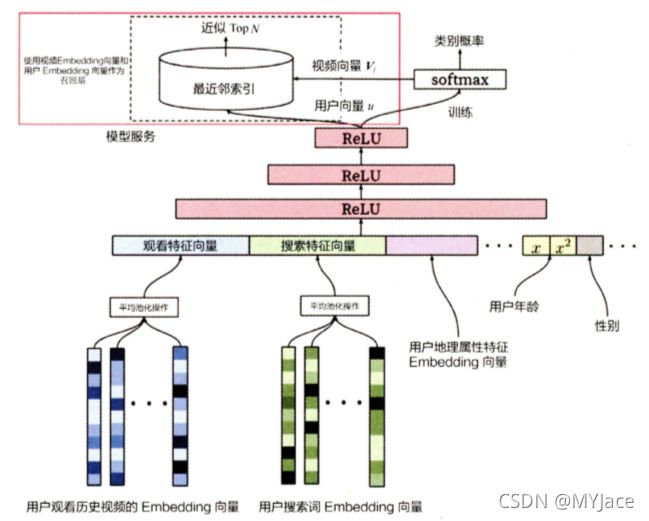
上图是 YouTube 推荐系统的召回模型。该模型的输入层是用户的相关特征，比如：用户观看历史视频的 Embedding 向量，用户搜索历史的 Embedding 向量，用户地理属性特征 Embedding 向量，用户年龄，用户性别等相关特征。

该模型本质上是一个多分类模型，它的输出层是 softmax 层。该层的输入是经过三层 ReLU 的用户 Embedding，它的输出向量是用户观看每个视频的概率分布。这个向量的每个维度对应一个视频，该维度对应的 softmax 层列向量就是视频 Embedding。通过离线训练，可以得到所有用户和视频的 Embedding。

在线上部署中，只需要将所有用户的 Embedding 以及视频 Embedding 保存在线上数据库，然后直接计算用户 Embedding 与视频 Embedding 内积即可得到一个推荐排序，这个排序结果取 Top N 就是召回的结果。也就是推荐漏斗的第一个初始候选集（从千万，百万级的海量物品库中，圈定了几千几百量级的候选集，大大缩小范围并且降低了计算量）。

局部敏感哈希 (LSH - Localicity Sensitive Hashing)

在用 Embedding 作为系统召回方法时，首先需要处理的问题就是在线上进行遍历内积运算时，由于数据量过大，计算时间可能会非常长。

这很好理解，因为在寻找最适合的推荐物品时，需要使用用户 Embedding 与候选集中的所有物品 Embedding 进行遍历，一一进行内积计算。如果 Embedding 空间（向量）维度为 k，共有 n 个物品，那么计算时间复杂度就是 O(kn)。

既然我们已经通过 Embedding 将用户 Embedding 以及物品 Embedding 置于同一个空间之中，那么，寻找最相似结果最直觉的方法就是在这个高维空间中使用最近邻搜索 (NN)。而局部敏感哈希 (LSH) 就是在高维空间中寻找最近邻的主流方法。

LSH 我在之前的笔记 Big Data Management笔记03：High Dimensional Similarity Search_MYJace的博客-CSDN博客 已经介绍过，这里只做简单的介绍：

LSH 的主要思想在于将相邻的点都置于同一个 Bucket 中。实现的方法就是让临近 (相似) 的点高概率有同样的 Hash Key，距离较远 (不相似) 的点高概率有不同的 Hash Key：

• 如果Dist(o₁，o₂) ≤ r₁，即o₁，o₂ 相似，则：

• 如果Dist(o₁，o₂) ＞ r₁ ，即o₁，o₂ 不相似，则：

  

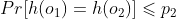
根据使用的距离 (Distance) / 相似度 (Similarity) 度量函数的不同，LSH 函数 h(·) 也会有区别。我们这里主要关注使用欧氏距离 (Euclidean Distance) 的 LSH 函数：P-Stable

在欧式距离中，当我们将高维的点映射到低维空间，会发生一个有趣的现象。原本在高维空间中靠近的点，仍会很近，而原本较远的点则有概率会靠近。

利用这种低维空间会保留高维空间临近距离关系的性质。就可以构造出 P-Satble LSH 函数。

假设 x 是一个高维空间中的 k 维向量，a 是一个随机生成的法向量 (Normal Vextor)。使用内积操作就可以将 x 映射为一个值：h(x) = a · x。此时就可以使用 P-Stable LSH 函数构建 Bucket：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CfP5K9fc-1630558980252)(E:\Deep Learning\推荐系统\Note\LSH.png)]

在这个函数中，a 和 b 都是超参数：

• a 已经说过，是一个随机生成的法向量，它的每个元素服从标准正态分布 a_i ~ N(0, 1)。
• b 服从均匀分布 b ~ U(0, 1)。它用来避免 Bucket 边界固化
• w 是用户定义的参数。表示 Bucket 宽度

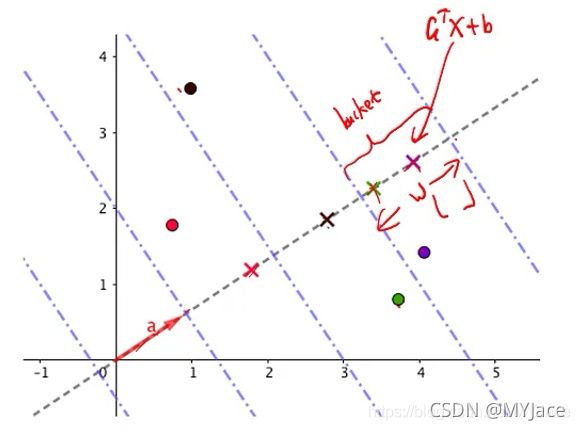
用一个图来理解：

图中的每个点就是一个data point，向量 a 上的 × 就是每个 data point 在其上的投影（projection），即为 a^Tx + b，蓝色虚线则为使用 floor 和 w 计算出的 Bucket，当两个 data points 的投影落在同一个 Bucket 中时，表示它们有相同的 hash key。因此，越接近（相似）的 data points，会有更高的几率被投射在同一个 Bucket 中

为了避免临近点误判，一般会选择使用多个 Hash 函数同时进行计算，在多个 P-Stable 中多次调入同一个 Bucket 的两个点为临近点的概率会大大提高。如此一来，直接在当前用户 Embedding 所在的 Bucket 中寻找最邻近物品 Embedding 即可。但是，在使用多个 Hash 函数时，我们需要权衡使用 “与” 和 “或” 的策略。

“与” 策略：对象 A 和对象 B 对应的点在多个 Hash 函数下，都落在同一个 Bucket 中，才认为二者相似。此时由于限定条件较为严格，因此准确率 (Precision) 会得到保障，同时候选集会相对小一些，减少了内积计算量。但是有可能会遗漏位于 Bucket 边界的对象。

“或” 策略：对象 A 和对象 B 在第一个 Hash 函数下落在同一个 Bucket 中，或在第二个 Hash 函数下落在同一个 Bucket 中。此时由于限定条件比较宽松，因此召回率 (Recall) 最终得到的候选集会比较大，这就意味着内积计算量仍会比较大