线性回归——局部加权线性回归
线性回归虽然简单,但是容易出现问题:就是“欠拟合”和“过拟合”,欠拟合是由于我们并不能很好的拟合我们的训练数据,导致出现较大的训练误差;而过拟合是由于我们过度拟合训练数据,导致我们的模型过度复杂而产生较大的测试误差。
如下图所示:左边的图就是欠拟合,很明显我们用直线是无法很好的拟合训练数据的,最右边的就是产生了过拟合,中间的曲线就是比较好的。
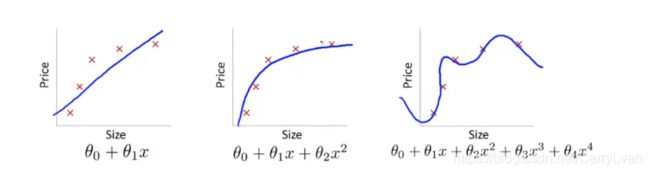
解决欠拟合我们可以增加额外的特征,或者增加多项式(如 x 2 x^2 x2之类的)。
接下来介绍一种解决欠拟合的方法——局部加权线性回归。
1.代价函数:
J ( θ ) = ∑ i = 1 m w ( i , i ) ( f ( x i ) − y i ) 2 J(\theta)=\sum_{i=1}^mw_{(i,i)}(f(x_i)-y_i)^2 J(θ)=i=1∑mw(i,i)(f(xi)−yi)2
其中 f ( x i ) f(x_i) f(xi)是我们的预测值, f ( x i ) = θ T x i f(x_i)=\theta^Tx_i f(xi)=θTxi; w ( i , i ) w_{(i,i)} w(i,i)是权重,它是通过要预测的点i与数据集中点的距离来确定的,距离越近, 权值越大,相应的误差值 ( f ( x i ) − y ) (f(x_i)-y) (f(xi)−y)影响就越大(可以达到增加多项式的效果),反之同理。我们通常使用如下的权重函数:
w ( i , i ) = e x p ( − ( x i − x ) 2 2 k 2 ) w_{(i,i)}=exp(-\frac{(x_i-x)^2}{2k^2}) w(i,i)=exp(−2k2(xi−x)2)
其中,x是我们的要预测的点,k是我们需要指定的参数,他控制了权值随距离变化的速率。
接下来我们可以通过梯度下降或者正规方程的方法来求解我们的 θ \theta θ,这里使用正规方程的解法,首先将我们的上面的代价函数写成矩阵的形式:
J ( θ ) = ( X θ − y ) T W ( X θ − y ) J(\theta)=(X\theta-y)^TW(X\theta-y) J(θ)=(Xθ−y)TW(Xθ−y)
其中X是我们的训练集,每一行是一个样本,y是我们的真实值,W是m大小的方阵,并且只有对角线上有值,其他地方都为0,(这里不懂得可以随便去一个样本大小为例子乘以下就知道了)。
最后我们就用对 J ( θ ) J(\theta) J(θ)关于 θ \theta θ求导,并令其为0求出我们的 θ \theta θ等于:
θ = ( X T W X ) − 1 X T W y \theta=(X^TWX)^{-1}X^TWy θ=(XTWX)−1XTWy
2.代码实现:
这里直接用了机器学习实战上面的实现代码
2.1算法实现:
from numpy import *
def lwlr(testPoint,xArr,yArr,k=1.0):
xMat = mat(xArr); yMat = mat(yArr).T
m = shape(xMat)[0]
weights = mat(eye((m))) #创建一个单位矩阵
for j in range(m):
diffMat = testPoint - xMat[j,:] #计算与数据集中其他点的距离
weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2)) #计算权重
xTx = xMat.T * (weights * xMat)
if linalg.det(xTx) == 0.0:
print("This matrix is singular, cannot do inverse")
return
ws = xTx.I * (xMat.T * (weights * yMat))
return testPoint * ws
def lwlrTest(testArr,xArr,yArr,k=1.0): #testArr是我们要预测的所有点的矩阵
m = shape(testArr)[0]
yHat = zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k) #对于每一个要预测的点都要重新计算权值
return yHat
2.2绘制结果:
from numpy import *
import matplotlib.pyplot as plt
import regression
xArr, yArr = regression.loadDataSet('data/Ch08/ex0.txt')
yHat = regression.lwlrTest(xArr,xArr,yArr,1.0)
xMat = mat(xArr)
srtInd = xMat[:,1].argsort(0)
xSort = xMat[srtInd][:,0,:]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xSort[:,1],yHat[srtInd])
ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0],s=2,c='red')
plt.show()
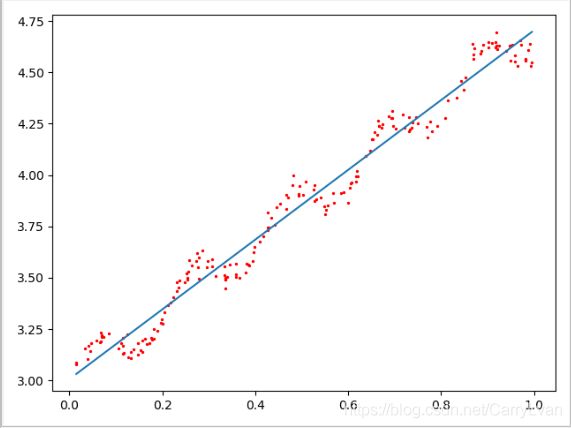
3.运行结果:
k=1.0(欠拟合):
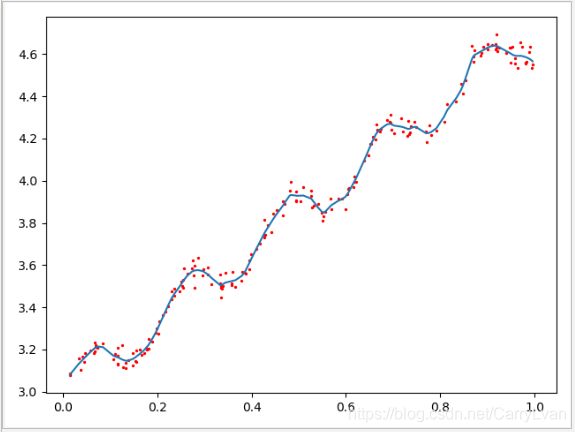
k=0.01(拟合的比较好):
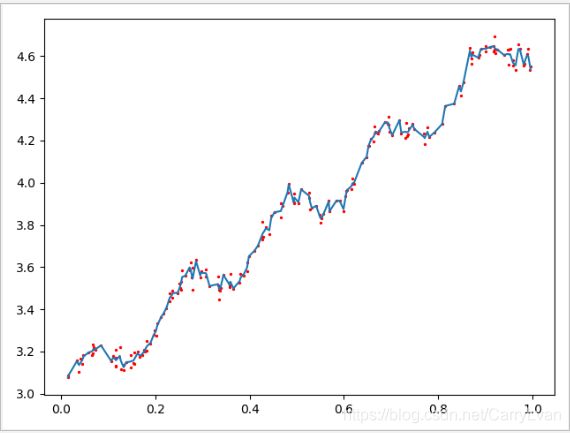
k=0.003(过拟合):
在调用上面代码时,我们通过会选取不同的k值,以获得最佳效果。
通过上面我们也知道每预测一个点,我们都要重新计算权重W矩阵,增加了我们的计算量。