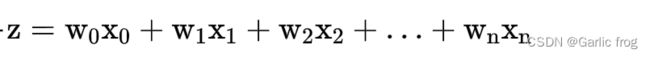Logistic回归

什么叫回归？

假设有一些数据点，我们用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就叫做回归。

Logistic回归的一般过程

​收集数据：采用任意方法收集数据
准备数据：由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳
分析数据：采用任意方法对数据进行分析
训练算法：计算不同独立特征的条件概率
测试算法：一旦训练步骤完成，分类将会很快
使用算法：首先需要输入一些数据，并将其转化成对应的结构化数值；接着，基于训练好的的回归系数就可以对这些数值进行简单的回归计算，判定他们属于哪个类别；
之后就可以在输出的类别上做出一些其他的分析工作。

基于Logistic回归和Sigmoid函数的分类

优点：计算代价不高，易于理解和实现
缺点：容易欠拟合，分类精度可能不高
适用数据类型：数值型和标称型数据

我们想要的函数，能接受所有的输入然后预测出类别。Sigmoid函数具有输出0或1的这种性质，而且在数学上容易处理。因此为了实现Logistic回归分类器，我们可以在每一个特征上都乘以一个回归系统，然后将所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。Sigmoid函数定义：

任何大于0.5的数据被分入1类，小于0.5的数据被归入0类。所以Logistic回归也可以看成是一种概率估计。

 基于最优化方法的最佳回归系数确定

Sigmoid函数的输入记为z，公式为：

上述公式可简化为z=W^T*X它表示数值向量对应元素相乘然后全部相加起来即得到z值。其中的向量x是分类器的输入数据，向量w是要求的最佳参数（系数），使分类器尽可能的精确。

 梯度上升法

梯度上升法基于的思想是要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。如果梯度记为∇，则函数f ( x , y )的梯度有下式表示：

这个梯度意味着要沿x的方向移动 ∂f(x,y)/∂x，沿y的方向移动∂f(x,y)/∂y，其中，函数f ( x , y )必须要在待计算的点上有定义并且可微。

上图中，梯度上升算法到达每个点后都会重新估计移动的方向。从 P0 开始，计算完该点的梯度，函数就根据梯度移动到下一点 P1。在 P1 点，梯度再次被重新计算，并沿着新的梯度方向移动到 P2 。如此循环迭代，直到满足停止条件。迭代过程中，梯度算子总是保证我们能选取到最佳的移动方向。
上图中的梯度上升算法沿梯度方向移动了一步。可以看到，梯度算子总是指向函数值增长最快的方向，这里说的是移动方向，而没有提到移动量的大小。该量值称为步长，记作α。用向量来表示梯度上升算法：

该公式将一直被迭代执行，直到达到某一停止条件为止。 

                                  梯度下降算法
我们最经常听到梯度下降算法，它与梯度上升算法是一样的，只是公式中加法变成减法。因此，公式为
                                  w:=w−α∇wf(w)
梯度上升算法用来求函数的最大值，而梯度下降算法用来求函数的最小值。

 代码实现：

数据集准备：

新建一个名叫testSet.txt的记事本存放数据集，第一列表示本部食堂堂食次数，第二列表示诚毅食堂堂食次数，第三列1表示学生宿舍在本部，0表示学生宿舍在诚毅。

训练算法：

from matplotlib import pyplot as plt
import numpy as ny
 
def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open('C:/Users/Administrator/Desktop/testSet.txt')
    for line in fr.readlines():                                 
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat
# sigmoid函数
def sigmoid(inX):
    return 1.0 / (1 + ny.exp(-inX))
 
# 梯度上升算法
def gradAscent(dataMatIn, classLabels):
    dataMatrix = ny.mat(dataMatIn)                                    
    labelMat = ny.mat(classLabels).transpose()                 
    m, n = ny.shape(dataMatrix)                               
    alpha = 0.01                                                 
    maxCycles = 500                                          
    weights = ny.ones((n, 1))                                      
    for k in range(maxCycles):                                 
        h = sigmoid(dataMatrix * weights)                        
        error = (labelMat - h)                                     
        weights = weights + alpha * dataMatrix.transpose() * error 
    return weights

 分析数据：画出决策边界

def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()                      
    dataArr = ny.array(dataMat)                              
    n = ny.shape(dataArr)[0]                                  
    xcord1 = []; ycord1 = []                            
    xcord2 = []; ycord2 = []                               
    for i in range(n):                                     
        if int(labelMat[i]) == 1:                         
            xcord1.append(dataArr[i, 1]); ycord1.append(dataArr[i, 2])
        else:                                              
            xcord2.append(dataArr[i, 1]); ycord2.append(dataArr[i, 2])
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=20, c='blue', marker='s')  
    ax.scatter(xcord2, ycord2, s=20, c='green')          
    x = ny.arange(1.0, 20.0, 0.01)                        
    y = (-weights[0] - weights[1] * x) / weights[2]    
    ax.plot(x, y)
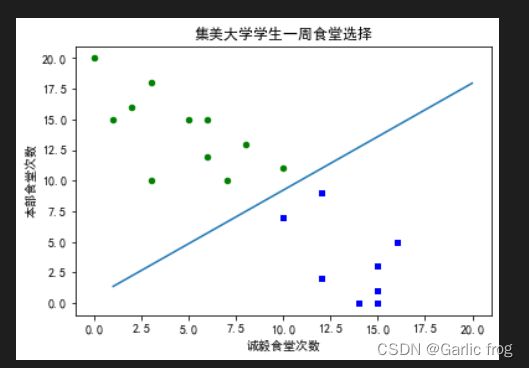
    plt.title('集美大学学生一周食堂选择')                                 
    plt.xlabel('诚毅食堂次数'); plt.ylabel('本部食堂次数')          
    plt.show()
dataMat, labelMat = loadDataSet()
weigths = gradAscent(dataMat, labelMat)
showData()
plotBestFit(weigths.getA())

运行结果：