【计算机图像处理】综合复习和习题
知识点及例题总结
- 一、导论
-
- 1.图像处理与图像分析
- 2.数字图像处理相关概念
- 二、数字图像处理基础
-
- 1.图像数字化的概念
- 2.点处理、局部处理、大局(全局)处理的相关算法
- 3.直方图的概念和性质
- 三、图像变换
-
- 1.图像平滑(低通滤波)的用途和缺点
- 2.图像锐化(高通滤波)的用途和缺点
- 3.伪彩色变换的概念及一种常用方法
- 4.假彩色变换的概念及一种变换方法
- 5.图像的噪声
- 四、图像增强
-
- 1.均值滤波和中值滤波的相同点和不同点
- 2.图像的加法和减法的应用
- 3.灰度变换
- 4.例题
- 五、图像复原与重建
-
- 1.例题
- 六、图像的编码与压缩
-
- 1.图像文件数据存储结构的种类及说明
- 2.图像的压缩标准
- 3.例题
- 七、图像分割
-
- 1.例题
- 八、二值图像处理与形状分析
-
- 1.标记
- 2.膨胀和收缩
- 3.边界跟踪
- 4.链码
- 5.例题
一、导论
1.图像处理与图像分析
(1)根据抽象程度与研究方法不同,可分为三个层次:图像处理、图像分析和图像理解。
(2)狭义上的图像处理:对图像进行加工以改善图像的视觉效果或突出有用的信息,或编码以减少对其所存储空间、传输时间或传输带宽的要求。特征:输入是图像,输出是图像,即图像间的变换。
(3)图像分析:对图像中感兴趣的目标进行检测(或分割)和测量,获得它们的客观信息,从而建立对图像的描述。特征:输入的是图像,输出的是数据。
2.数字图像处理相关概念
(1)概念:用计算机对数字图像进行系列操作,从而获得某种预期结果的技术,叫做数字图像处理。
(2)内容:图像的数字化、图像变换、图像增强、图像的恢复与重建、二值图像的处理与分析、纹理分析、图像识别
(3)数字图像处理系统的组成:采集、显示、存储、通信、主机、图像处理软件。
(4)数字图像处理系统的特点:精度高,再现性好,通用性、灵活性强。
(5)数字图像处理的应用:生物医学、遥感、工业、军事、通信、公安等领域。
二、数字图像处理基础
1.图像数字化的概念
(1)定义:将一幅画面转化为计算机能处理的形式——数字图像的过程。
(2)过程:
①采样:将空间上连续的图像变换成离散的点的操作。
②量化:将采样图像被分割成空间上离散的像素,但其灰度是连续的,还不能用计算机进行处理,将像素灰度转化为离散的整数值的过程叫做量化。
(3)采样和量化的分析(从质量和数据量两方面分析)
①采样间隔大的图像像素数少,空间分辨率低,质量差、严重时呈现块状国际棋盘效应,但数据量小。采样间隔小的图像像素数多,空间分辨率高,质量好,但数据量大。
②量化等级少的图像层次欠丰富、灰度分辨率低、有假轮廓现象,但数据量小。量化等级多的图像层次丰富、灰度分辨率高、质量好,但数据量大。
2.点处理、局部处理、大局(全局)处理的相关算法
(1)点处理:线性灰度变换、分段线性灰度变换、直方图修正法。
(2)局部处理:局部平滑法、灰度最相近的K个邻点平均法、超限像素平滑法、中值滤波法、空间低通滤波法。
(3)全局处理:傅里叶变换。
3.直方图的概念和性质
(1)概念:反映一幅图像中各灰度级像素出现的频率之间的关系。
(2)性质:
①灰度直方图只能反映图像的灰度分布情况,不能反映图像的像素位置,即丢失了像素的位置信息。
②一幅图像对应唯一的灰度直方图,反之不成立。不同的图像可以对应相同的直方图。
③一幅图像分成了多个区域,多个区域的直方图之和即为原图像的直方图。
三、图像变换
1.图像平滑(低通滤波)的用途和缺点
(1)用途:图像平滑的主要用途是消除图像中的噪声。
(2)负面影响:由于平滑算子实质上是一种低通滤波器,且图像中的边缘反映的是图像中的细节和高频信息,所以在利用邻域平均法进行图像平滑或利用低通滤波进行图像消噪的同时,会使边缘变得模糊。并且,进行图像平滑的模板大小与图像平滑的效果密切相关,模板尺寸越大,平滑后的图像越模糊。
2.图像锐化(高通滤波)的用途和缺点
(1)用途:图像锐化主要用于突出和加强图像中景物的边缘和轮廓。
(2)负面影响:由于锐化算子是一种高通滤波器,通过图像锐化在增强图像边界和细节的同时,也使噪声得到加强,另外,各向异性算子由算子中间一行一列两边元素的相反值特征,会使锐化后的图像的边缘比较粗,因此进行图像锐化处理应有较高的信噪比,否则经锐化后的图像质量会进一步降低。
3.伪彩色变换的概念及一种常用方法
(1)伪彩色变换:把一幅灰度图像的各个不同灰度级按照线性或非线性的影射函数变换成不同彩色,得到一幅彩色图像的技术。
(2)密度分割法:把图像灰度级从黑到白分成N个区间,给每个区间指定一种颜色得到灰度颜色对照表,然后按表查询颜色值。
4.假彩色变换的概念及一种变换方法
(1)假彩色变换:通过映射函数将彩色图像或多光谱图像变换成新的三基色分量,经彩色合成在增强图像中的各目标呈现出与原图像中不同彩色的技术。
(2)线性假彩色映射法:将原来的三基色转变为另一种三基色分量。

上述例子中,绿色将变为红色,蓝色将变为绿色,红色将变为蓝色。
5.图像的噪声
(1)图像两种典型的噪声是:椒盐噪声和高斯噪声
(2)椒盐噪声:由图像传感器、传输信道、解码处理等产生黑白相间的亮暗点噪声幅值相同,出现点随机,用中值滤波效果好,不属于加性或乘性噪声。
(3)高斯噪声:图像上每一点都存在噪声、但噪声位置是随机分布的,用均值滤波的效果好,属于加性噪声。
四、图像增强
1.均值滤波和中值滤波的相同点和不同点
(1)相同点:都可以起到平滑图像、滤去噪声的功能。
(2)不同点:
①均值滤波:线性方法,但不能很好的保护图像的细节,会使图像变得模糊,对高斯噪声表现好。
②中值滤波:非线性方法,平滑脉冲噪声有效,保护图像边缘,但可能使边缘较粗,对椒盐噪声表现好
2.图像的加法和减法的应用
(1)加法:叠加高斯噪声灰度图像用多图像平均分法消除随机噪声
(2)减法:测变化及运动的物体、背景消除、目标识别、动态监测、运动目标检测和跟踪。
3.灰度变换
灰度变换可调整的图像的灰度动态范围或图像的对比度,是图像增强的重要手段之一。
4.例题
(1)某像素5×5邻域的灰度分布如图,经计算9个掩模区的
均值和方差为
| 均值 | 4 | 4 | 3 | 2 | 3 | 4 | 2 | 3 | 3 |
|---|---|---|---|---|---|---|---|---|---|
| 均值对应的方差 | 54 | 7 | 17 | 17 | 28 | 31 | 23 | 26 | 0 |

若采用有选择保边缘平滑法,该像素的输出值为(3)
解:最小方差为0,对应的灰度均值3,采用有选择保边缘平滑,该像素的输出值为3。
(2)采用有选择保边缘平滑法抑制噪声,对于像素点(5,4),经计算9个掩模区的均值和方差如下:
| 均值 | 4 | 4 | 3 | 2 | 3 | 4 | 5 | 3 | 3 |
|---|---|---|---|---|---|---|---|---|---|
| 均值对应的方差 | 54 | 7 | 17 | 17 | 28 | 31 | 1 | 26 | 25 |
该点的输出值为(5)
解:最小方差为1,对应的灰度均值5,采用有选择保边缘平滑,该像素的输出值为5。

(3)1.下图是一副噪声图像,请用以下方法对其进行处理,要求简述个方法原理,并写出结果。
①.4-邻域平滑法。
解:
80(2,2)的值是4-邻域的均值即:(12+21+86+80)/4=49.75≈50
80(2,3)的值是4-邻域的均值即:(8+10+88+80)/4=46.5≈47
86(3,2)的值是4-邻域的均值即:(28+26+88+80)/4=55.5≈56
88(3,3)的值是4-邻域的均值即:(80+25+30+86)/4=55.25≈55
得到的结果是:
| 12 | 12 | 10 | 10 |
|---|---|---|---|
| 21 | 50 | 47 | 8 |
| 26 | 56 | 55 | 25 |
| 28 | 28 | 30 | 26 |
②.超限像素平滑法,T=20。
解:
80(2,2)的4-邻域的均值即:(12+21+86+80)/4=49.75≈50
80-50=30 > 20 取均值
80(2,3)的4-邻域的均值即:(8+10+88+80)/4=46.5≈47
80-47=33 > 20 取均值
86(3,2)的4-邻域的均值即:(28+26+88+80)/4=55.5≈56
86-56=30 > 20 取均值
88(3,3)的4-邻域的均值即:(80+25+30+86)/4=55.25≈55
88-55=33 > 20 取均值
得到的结果是:
| 12 | 12 | 10 | 10 |
|---|---|---|---|
| 21 | 50 | 47 | 8 |
| 26 | 56 | 55 | 25 |
| 28 | 28 | 30 | 26 |
③.灰度最相近的K个邻点平均法,其中采用3*3邻域,K=5。
解:
80(2,2)的值是5个相近值的均值即:(26+21+88+86+80)/5=60.2≈60
80(2,3)的值是5个相近值的均值即:(25+86+88+80+12)/5=58.2≈59
86(3,2)的值是5个相近值的均值即:(28+30+88+80+80)/5=61.2≈61
88(3,3)的值是5个相近值的均值即:(80+80+28+30+86)/5=60.8≈61
得到的结果是:
| 12 | 12 | 10 | 10 |
|---|---|---|---|
| 21 | 60 | 59 | 8 |
| 26 | 61 | 61 | 25 |
| 28 | 28 | 30 | 26 |
④3*3模板中值滤波
解:
80(2,2)的值是3x3网格内的中值即:10 12 12 21 26 80 80 86 88
80(2,3)的值是3x3网格内的中值即:8 10 10 12 25 80 80 86 88
86(3,2)的值是3x3网格内的中值即:21 26 28 28 30 80 80 86 88
88(3,3)的值是3x3网格内的中值即:8 25 26 28 30 80 80 86 88
得到的结果是:
| 12 | 12 | 10 | 10 |
|---|---|---|---|
| 21 | 26 | 25 | 8 |
| 26 | 30 | 30 | 25 |
| 28 | 28 | 30 | 26 |
(4)假定有64x64大小的图像,灰度级为16级,概率分布如下表,试进行直方图均衡化。
| r | nk | pr(pk) |
|---|---|---|
| r0=0 | 800 | 0.195 |
| r1=1/15 | 650 | 0.160 |
| r2=2/15 | 600 | 0.174 |
| r3=3/15 | 430 | 0.106 |
| r4=4/15 | 300 | 0.073 |
| r5=5/15 | 230 | 0.056 |
| r6=6/15 | 200 | 0.049 |
| r7=7/15 | 170 | 0.041 |
| r8=8/15 | 150 | 0.037 |
| r9=9/15 | 130 | 0.031 |
| r10=10/15 | 110 | 0.027 |
| r11=11/15 | 96 | 0.023 |
| r12=12/15 | 80 | 0.019 |
| r13=13/15 | 70 | 0.017 |
| r14=14/15 | 50 | 0.012 |
| r15=1 | 30 | 0.007 |
(5)假定有64x64的8bit数字图像,灰度级出现频率如表1,要求将此幅图像进行直方图变换,使其变换后具有表2的灰度分布。
| 表1 f(x,y) | nk | pr(pk) |
|---|---|---|
| 0 | 560 | 0.14 |
| 1 | 920 | 0.22 |
| 2 | 1046 | 0.26 |
| 3 | 705 | 0.17 |
| 4 | 356 | 0.09 |
| 5 | 267 | 0.06 |
| 6 | 170 | 0.04 |
| 7 | 72 | 0.02 |
| 表2 g(x,y) | nk | pr(pk) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 2 | 0 | 0 |
| 3 | 790 | 0.19 |
| 4 | 1023 | 0.25 |
| 5 | 850 | 0.21 |
| 6 | 985 | 0.24 |
| 7 | 448 | 0.11 |
五、图像复原与重建
1.例题
(1)若f(31,46)=18、f(31,47)=26、f(32,46)=20、f(32,47)=10, g(25, 26)和f(31.4,46.8)是对应点,按双线性插值法确定g(25, 26)的灰度值为(19)。按最近邻元法确定f(31.4,46.8)的灰度值为(26) 。
解:
双线性插值法确定g(25,26)=(1-u)(1-v) f (i, j) +(1-u)vf (i, j +1) +u(1- v) f (i +1, j) +uvf (i +1, j +1),其中,u=31.4-31=0.4,v=46.8-46=0.8,因此g(25,26)=0.6x0.2x18+0.6x0.8x26+0.4x0.2x20+0.4x0.8x10=19.44≈19
最近邻元法是将在待求点的四邻像素中,将距离这点最近的相邻像素,灰度赋给该待求点。距离f(31.4,46.8)最近的灰度值为f(31,47)=26.
六、图像的编码与压缩
1.图像文件数据存储结构的种类及说明
(1)组合方式:一个字长存放多个像素值的方式。
(2)比特面方式:按比特位存取像素,即将所有像素的相同比特位用一个二维数组表示,形成比面。
(3)分层结构:由原始图像开始依次构成像素数越来越少的一幅幅图像,就能使数据结构表示具有分层性。
(4)树结构:对于一幅二值图像的行、列接连不断的不断二等分,如果图像被分割部分中,全体像素都变成具有相同的特征时,这一部分则不再分割。
(5)多重图像数据存储:①逐波段存储;②逐行处处;③逐像素存储。
2.图像的压缩标准
(1)静态图像压缩标准:JPEG(Joint Picture Expert Group)格式即联合图像专家组, 是由ISO和CCITT为静态图像所建立的第一个国际数字图像压缩标准,1991年开始使用。
(2)动态图像压缩标准:MPEG(Moving Pictures Experts Group)的任务是制定用于数字存储媒质中活动图像及伴音的编码标准。MPEG与JPEG算法在概念上类似,只不过它还利用了相继图像之间的冗余信息。
(3)二值图像压缩标准:JBIG(Joint Bilevel Imaging Group)的任务是研究制定用于二值图像的编码标准。该标准主要是为二值传真图像应用而设计的。
3.例题
(1)已知一幅图有8个灰度等级,分别用符号a0、a1、a2、…、a7表示,它们在图中出现的频率依次是0.07、0.24、0.1、0.40、0.03、0.06、0.02、0.08,请对这组符号分别按以下要求进行编码:
①霍夫曼(Huffman)编码,并计算平均码长;
②费诺-香农(Fano-Shannon)编码,并计算压缩比。

(2)对一信号源进行解码,已知字符a的概率为0.3,区间为[0.0,0.3),字符b的概率为 0.5,区间为[0.3, 0.8),字符c的概率为 0.2,区间为[0.8,1.0),若可用0.5表示该长度为2的信号源,则该信号源为(B)。
A. ba B. bb C. ab D.ca
(3)第2题中,若前提相同,此时用0.5表示长度为3的信号源,则该信
号源为(B)。
A. bab B. bba C. abc D.cab

(4)列举多重图像数据存储常用的三种存储方式,该三种方式分别对以下图1的RGB彩色图像进行存储。

第一种方式:逐波段存储
存储结果:128 220 70 95 10 20 30 40 100 110 120 130
第二种方式:逐行存储
存储结果:128 220 10 20 100 110 70 95 30 40 120 130
第三种方式:逐像素存储
存储结果:128 10 100 220 20 110 70 30 120 95 40 130
(5)有一信源X,其中:P1=0.20,P2=0.09,P3=0.11,P4=0.13,P5=0.07,P6=0.12,P7=0.08,P8=0.20,试将其进行霍夫曼编码,并计算信源的熵、平均码长、编码效率及冗余度,若采用二叉树编码,请画出二叉树。

七、图像分割
1.例题
1.【阈值分割】黑色背景上有两个没有接触的白色正方体A和B,在其正上方进行拍摄,获取的图像用16级灰度图像表示,该图像的直方图如下所示,设像素间距是1mm,已知A的体积是B的体积的8倍,试问A、B的体积各为多少? 要求写出计算和分析过程。[0 100 500 2000 0 137 225 375 700 1626 700 375 225 137 0 0]
解:立方体的上面投影图类似于下图,观察直方图分布,可以找到波谷且靠近灰度级较高的部分是白色的正方体,因此,白色像素总和可估计为:137+225+375+700+1626+700+375+225+137=4500px,A的体积是B体积的8倍,正方体体积公式为V=a3,因此RA:RB=2:1,SA:SB=4:1,因此SA=3600px,SB=900px,RA=60px,RB=30px,已知像素间距为1mm,VA=216cm3,VB=27cm3

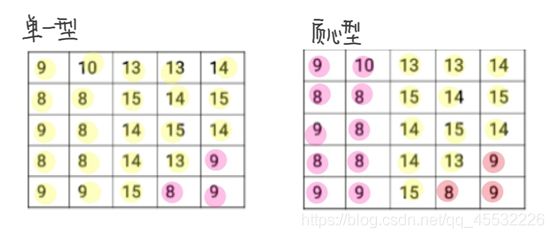
2.【区域划分】对下列图像采用单一型和质心型两种方法进行处理,T=3.5。

八、二值图像处理与形状分析
1.标记
为区分连接成分,求得连接成分的个数,连接成分的标记必不可少。对属于同一个1像素连接成分的所有像素分配相同的编号,对不同的连接成分分配不同编号的处理,叫做连接成分的标记。
2.膨胀和收缩
(1)膨胀:把二值图像各1像素连接成分的边界扩大一层的处理。像元f(i,j)或其4-/8-邻域的一个像素为1时,g(i,j)=1.
(2)收缩(腐蚀):把二值图像各1像素连接成分的边界点去掉从而缩小1层的处理。像元f(i,j)或其4-/8-邻域的一个像素为0时,g(i,j)=0.
3.边界跟踪
为了求区域间的连接关系,必须沿区域的边界点跟踪像素,称之为边界(或边缘)跟踪。
4.链码
5.例题
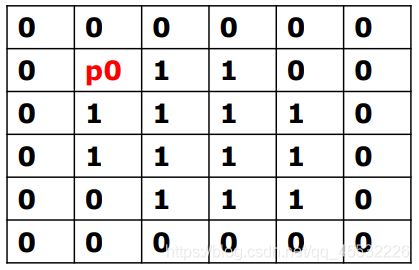
(2)对下图进行边界跟踪,并从P0点开始写出边界的链码,计算链码的长度。若将边界的像素总和作为周长,求图像的周长和面积。
解:

根据链码的定义,表示出从P1 的链码为6670022344,其中偶数8个,奇数有2个,链码长度为8+2√2.
将边界的像素总和作为周长,则周长为:10,面积为:14
(3)绘出链码为22222255500的曲线,计算该曲线长度
解:

根据链码的定义,表示出从P1 的链码为22222255500,其中偶数8个,奇数有3个,链码长度为8+3√2。