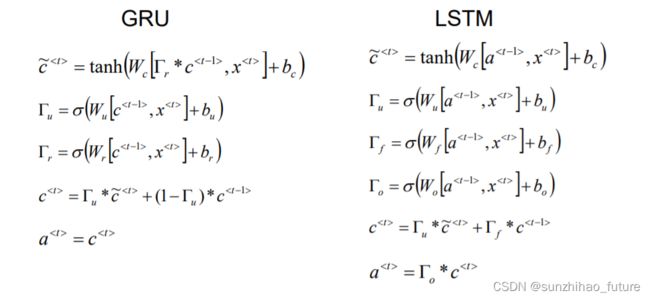高级人工智能(国科大2021-2022秋季学期课程)-基础概念及算法
高级人工智能-沈华伟-国科大2021-2022秋季学期课程
- 连接主义(神经网络、深度学习)
-
- 搜索问题
-
- 启发式算法
-
- 贪婪最佳优先搜索
- A*搜索
-
- A*树搜索
- A*图搜索
- 传教士和野人问题
- 归结原理中的应用
- 神经网络
-
- 传统神经网络
-
- 多层感知机(Multi-Layer Perceptron)
- 计算机视觉的深度学习模型
-
- 残差网络(Residual Networks, ResNets)
- 序列数据的深度学习模型
-
- 循环神经网络(Recurrent Neural Networks, RNN)
- GRU and Long Short Term Memory(LSTM)
- 生成式对抗网络(Generative adversarial networks, GAN)
- 图神经网络
- 符号主义(数理逻辑)
-
- 命题逻辑(Propositional Logic)
-
- 语法与逻辑推导(Syntax and Derivation)
- 语义与形式推演(Semantics and Deduction)
-
- 形式推演的11条规则(一种形式推演系统)
- 归结原理(Resolution)
-
- 转化为CNF合取范式
- 可靠性(Soundness)
- 完备性(Completeness)
- Modus Ponens规则
-
- 前向推理(Forward chaining)
- 后向推理(Backward Chaining)
- 可靠性(Soundness)
- 完备性(Completeness)
- 一阶谓词逻辑(First-order Logic)
-
- 语法与逻辑推导(Syntax and Derivation)
- 语义与形式推演(Semantics and Deduction)
-
- 合一化算子(Unification)
- 归结原理(Resolution)
-
- 转化为CNF合取范式
- 归结策略:广度优先
- 归结策略:删除策略与限制策略
- Generalized Modus Ponens (GMP) 规则
-
- 前向推理与后向推理
- 模糊逻辑
-
- 模糊集
-
- 模糊集的表示
- 模糊集的运算
- 模糊关系
- 模糊逻辑
- 行为主义(强化学习)
-
- 群体智能
-
- 蚁群算法
- 粒子群算法
- 强化学习
-
- 格子游戏
- 博弈
-
- 基本概念
- 田忌赛马
声明: 部分图片来自于课程讲义,(沈华伟,罗平)
连接主义(神经网络、深度学习)
搜索问题
启发式算法
启发式搜索(Heuristically Search)是利用问题拥有的启发信息来引导搜索,达到减少搜索范围、降低问题复杂度的目的,这种利用启发信息的搜索过程称为启发式搜索。其代表算法为:贪婪最佳优先搜索(Greedy Best-First Search)和A*搜索。
评价函数f(n)描述的是从当前节点出发,根据评价函数来选择后续节点。
启发函数h(n)描述的是从计算节点到目标节点之间所形成路径(耗散)的最小代价值。
贪婪最佳优先搜索
在贪婪最佳优先搜索算法里面,评价函数f(n)等于启发函数h(n)。贪婪最佳优先搜索不是最优的,也不是完备的。
A*搜索
A*树搜索
启发函数 h ( n ) h(n) h(n)是可采纳的,那么
0 ≤ h ( n ) ≤ h ⋆ ( n ) 0 \leq h(n) \leq h^{\star}(n) 0≤h(n)≤h⋆(n)
其中 h ⋆ ( n ) h^{\star}(n) h⋆(n)是到最近目标的真实耗散,即估计的耗散小于到最近目标的实际耗散。
A*树搜索算法最优性的条件是启发函数 h ( n ) h(n) h(n)是可采纳的,证明如下:
令A为最优目标节点,B为次优目标节点,并且 h ( n ) h(n) h(n)是可采纳的,要证明A在B之前离开边缘集合。
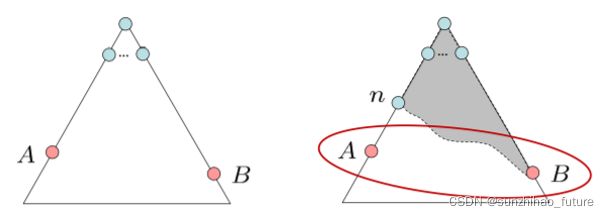
假设B在边缘集合中,A的某个祖先节点n(可能包括A)也在边缘集合中,
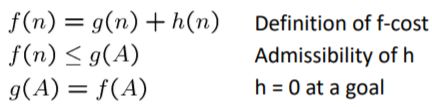
所以 f ( n ) ≤ f ( A ) f(n) \leq f(A) f(n)≤f(A),

所以 f ( n ) ≤ f ( A ) < f ( B ) f(n) \leq f(A) < f(B) f(n)≤f(A)<f(B),
所以A的所有祖先在B之前扩展,A在B之前扩展,因此A*树搜索算法是最优的。
通常,可采纳启发函数是松弛问题的解的耗散。
A*图搜索
启发函数 h ( n ) h(n) h(n)是一致的,那么
h ( A ) − h ( C ) ≤ h(A) - h(C) \leq h(A)−h(C)≤ actual cost(A to C)
即对于图中的每一条弧,估计的耗散都小于实际的耗散。
A*图搜索算法最优性的条件是启发函数 h ( n ) h(n) h(n)是一致的,证明如下:


实话说,这些证明我没看懂,我的问题,老师上课也是读了一遍slide,与我无关……
启发函数的一致性暗示了可采纳性,通常天然的可采纳启发函数是倾向于一致的,特别是从松弛问题中获得的启发函数。
传教士和野人问题
[例题]
传教士missionary和野人caveman问题通常描述如下: 三个传教士和三个野人在河的一边,还有一条能载一个人或者两个人的船,找到一个方法让所有的人都渡到河的另一岸,要求在任何地方野人数都不能多于传教士的人数,可以只有野人没有传教士。
(1) 精确地形式化该问题,只描述确保该问题有解所必须的特性,画出该问题的完全状态图.
(2) 用一个合适的算法实现和最优地求解该问题,检查重复状态是个好主意嘛?
(3) 这个问题的状态空间如此简单,为什么求解却很困难?
本题答案部分来源于网络,有待确定!

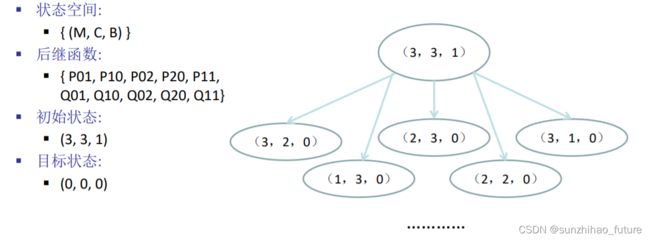
完全状态图:
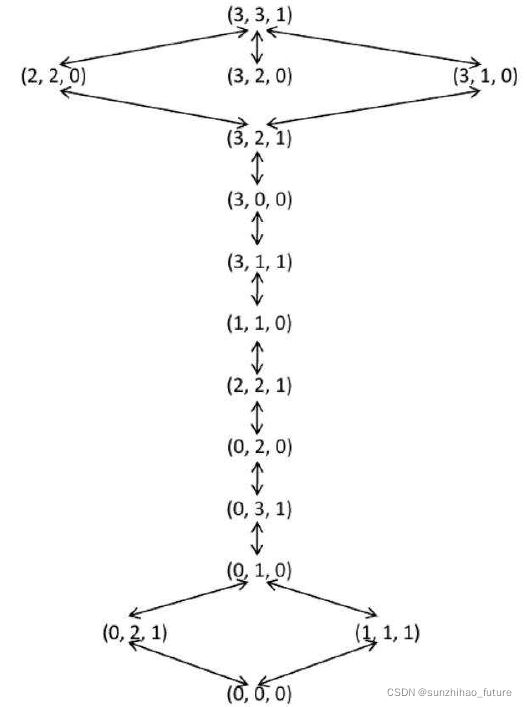

应该注意检查重复状态,能够避免进入死循环。
虽然状态空间比较简单,但是检查重复状态是一项困难的工作;并且列举当前状态所有合法的后继状态也很困难,包括无合法后继状态后的回溯问题。
归结原理中的应用
[例题]
应该如何设计A*启发式函数使得归结次数最少?
h ( n ) h(n) h(n) = minimal length of clause in this set.
神经网络
传统神经网络
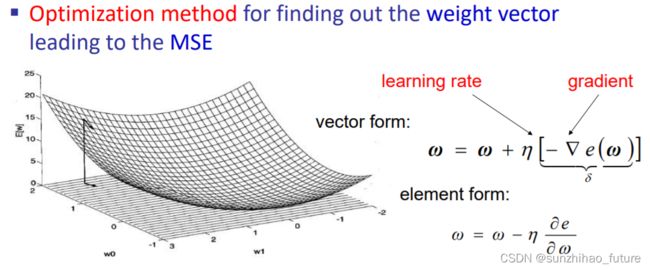
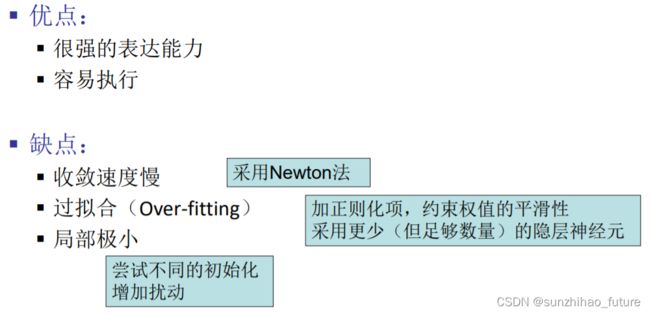
多层感知机(Multi-Layer Perceptron)
多层感知机特性:
- 多层感知机层间神经元全连接。
- Can represent AND, OR, NOT, etc., but not XOR.
- 若训练数据集是线性可分的,则感知机模型收敛。
计算机视觉的深度学习模型
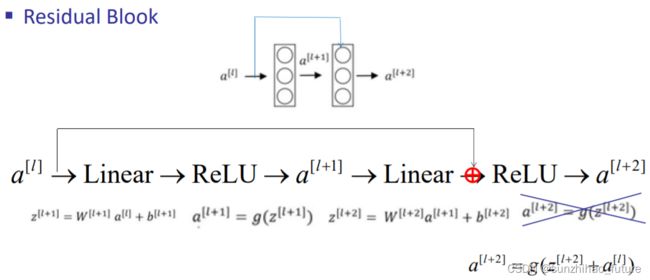
残差网络(Residual Networks, ResNets)
序列数据的深度学习模型
循环神经网络(Recurrent Neural Networks, RNN)
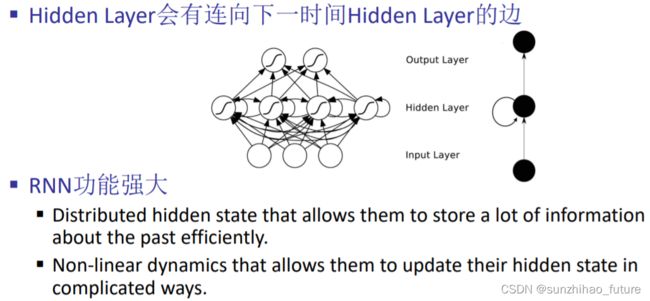
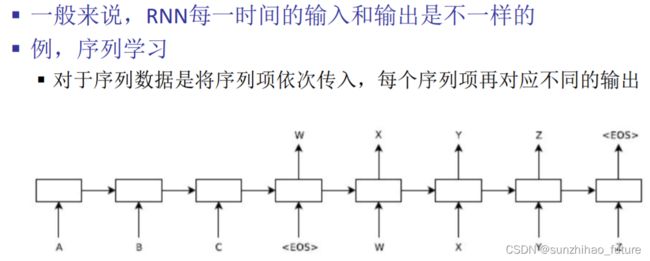
使用BPTT(Back Propagation Through Time)算法训练循环神经网络RNN。
GRU and Long Short Term Memory(LSTM)
生成式对抗网络(Generative adversarial networks, GAN)
GAN的核心思想来源于博弈论的纳什均衡。GAN包括一个生成器(Generator)和一个判别器(Discriminator),生成器的目的是尽量去学习真实的数据分布,判别器的目的是尽量正确判别输入数据是来自真实数据还是来自生成器生成的数据。


图神经网络
符号主义(数理逻辑)
逻辑研究的内容:
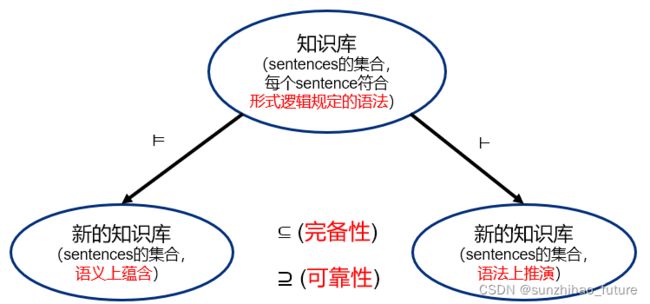

KB ⊨ α \text{KB} \models \alpha KB⊨α的等价描述:
- M o d e l ( KB ) ⊆ M o d e l ( α ) Model(\text{KB}) \subseteq Model(\alpha) Model(KB)⊆Model(α)
- KB ⇒ α \text{KB} \Rightarrow \alpha KB⇒α is valid(永真)
- KB ∧ ¬ α \text{KB} \land \lnot \alpha KB∧¬α is unsatisfiable(不可满足)
命题逻辑(Propositional Logic)
语法与逻辑推导(Syntax and Derivation)
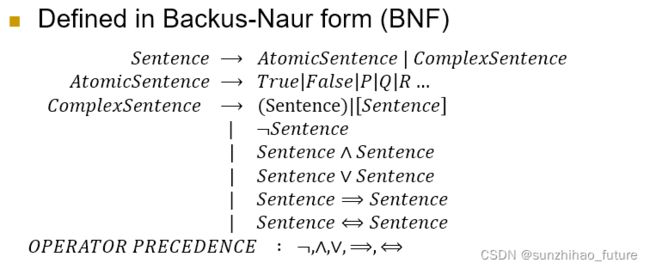
Entailment以及Implication的区别: Entailment是逻辑上的概念,刻画两组sentence之间的关系;Implication是命题proposition之间的一种算子,使用真值表刻画其语义。


命题逻辑中的知识库KB为满足命题逻辑语法的sentence的集合,假设在这组sentence中,一共有n个原子命题,对每个原子命题赋值称为真值指派,一共有 2 n 2^n 2n种真值指派,其中:使得KB中的每个sentence都为真的真值指派,就是KB的model。在此基础上,在命题逻辑中,可以明确的定义KB ⊨ α \models \alpha ⊨α。

语义与形式推演(Semantics and Deduction)
形式推演的11条规则(一种形式推演系统)
归结原理(Resolution)
转化为CNF合取范式

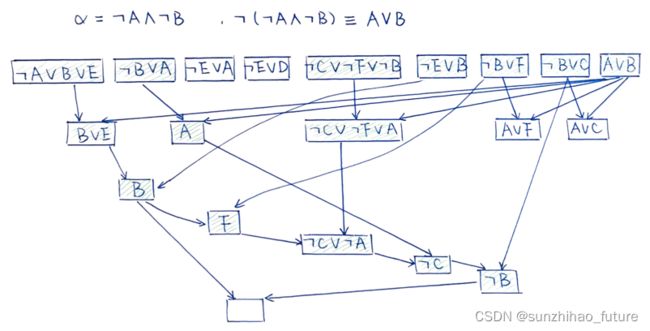
Resolution归结原理证明KB ⊢ α \vdash \alpha ⊢α:


证明KB ⊢ α \vdash \alpha ⊢α举例:
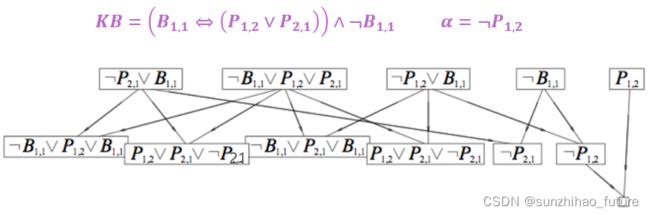
需要注意:两个子句根据归结原理可以推出多个不同的子句。
可靠性(Soundness)
在研究可靠性与完备性问题时,应当把语法层面的知识理解为Groundtruth,因此可靠性可以大概表述为:语义上推演得到的知识在语法上正确。因此要证明归结原理的可靠性,即证明:
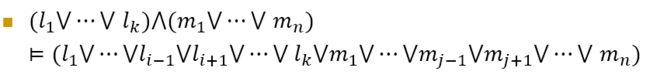
可靠性的证明使用真值表即可。
完备性(Completeness)
完备性可以大概表述为:如果语法上能够推理得到的,那么语义上正确。



Modus Ponens规则
上述提到的归结原理具有完备性,这是很好的性质,对于许多现实世界的应用,如果添加一些限制,可以实现更高效的推理。为了换取更好的inference的时间效率,缩小命题逻辑propositional logic的表达范围,得到适用于Horn Form的Modus Ponens规则,是另外一种形式的归结原理。

Modus Ponens规则可以使用Forward Chaining or Backward Chaining,这些算法易于理解,并且时间复杂度为线性时间。
前向推理(Forward chaining)
前向推理的核心思想是:触发所有前提(前件)存在于知识库中的规则,将其结论(后件)添加到知识库中,直到完成查询query。

前向推理算法执行过程举例如下:
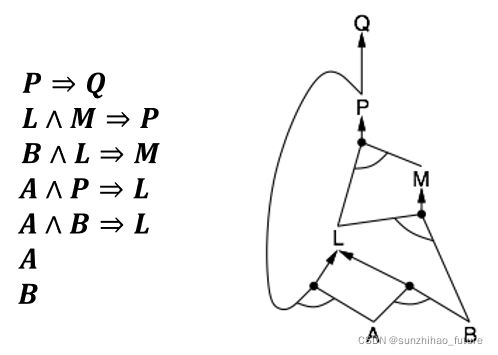
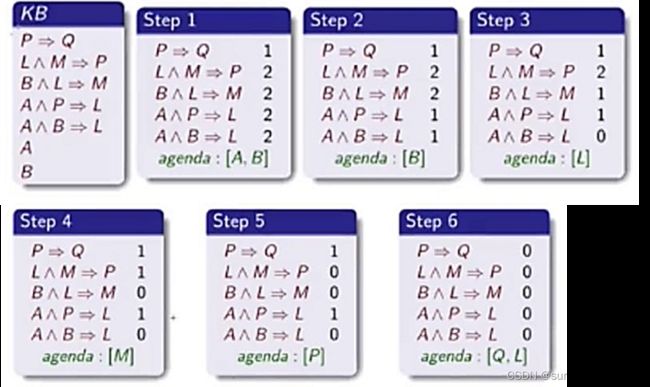
后向推理(Backward Chaining)

Forward Chaining以及Backward Chaining的比较:

可靠性(Soundness)
完备性(Completeness)
一阶谓词逻辑(First-order Logic)
语法与逻辑推导(Syntax and Derivation)
语义与形式推演(Semantics and Deduction)
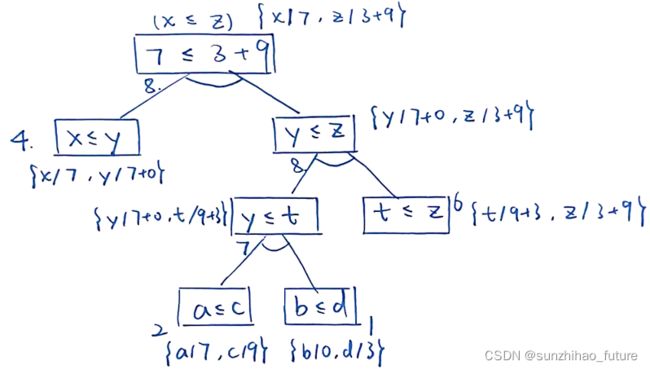
合一化算子(Unification)
归结原理(Resolution)
转化为CNF合取范式
归结策略:广度优先
广度优先策略的优点:当问题有解时保证能找到最短归结路径;是一种完备的归结策略。
广度优先策略的缺点:归结出了许多无用的子句;既浪费时间,又浪费空间。
广度优先对大问题的归结容易产生组合爆炸,但对小问题却仍是一种比较好的归结策略。
归结策略:删除策略与限制策略
删除策略是通过删除某些无用的子句来缩小归结范围。限制策略是通过对参加归结的子句进行某些限制,来减少归结的盲目性,以尽快得到空子句。
Generalized Modus Ponens (GMP) 规则
前向推理与后向推理
模糊逻辑
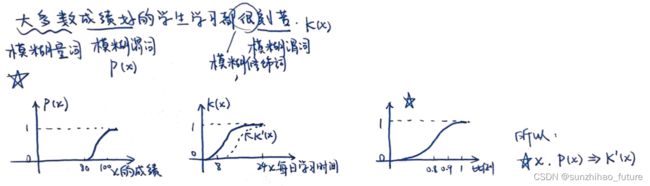
首先需要明确,模糊性的概念为对象从属的界限是模糊的,随判断人的思维而定。模糊性描述的是事件发生的程度,而不是一个事件是否发生;而随机性描述的是事件发生的不确定性,即一个事件发生与否。
模糊集
模糊集的表示
模糊集的运算
模糊关系
模糊逻辑
行为主义(强化学习)
群体智能
蚁群算法
粒子群算法
强化学习
格子游戏
[例题]
假如玩家采用的策略是在每个格子以等概率选择上下左右四个方向进行移动,每移动一步的收益是-1,移动到出口时游戏结束,如果当前移动会导致出界,那么移动后位置不变.
(1) 策略评估: 请使用动态规划方法计算出当前策略下每个格子对应的状态估值.
(2) 策略提升: 写出上述估值函数对应的贪心策略.
(3) 最优策略: 求解该问题的最优策略以及相应的状态估值.



[例题]
更正:下面的贝尔曼方程中的符号有错误,但是结果正确,方程形式以上题为准!

博弈
基本概念
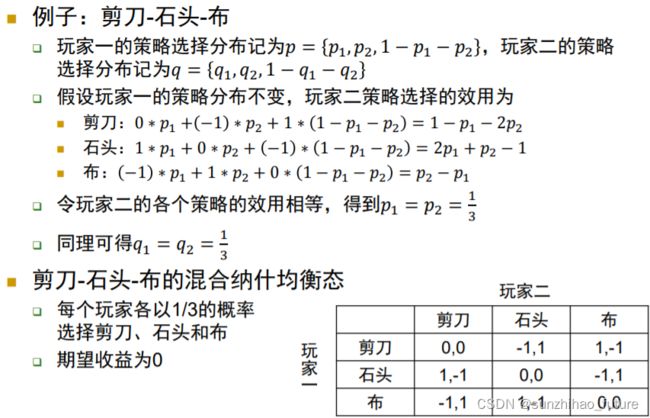
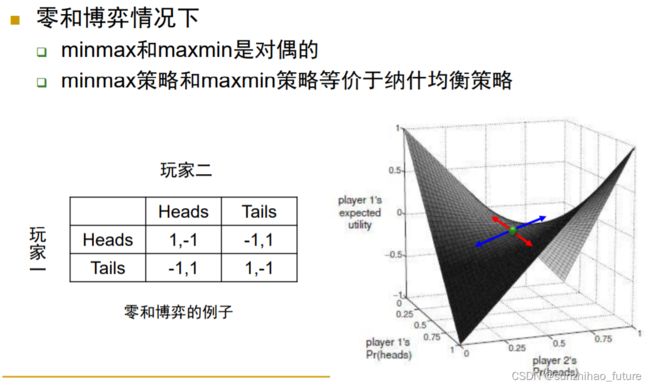
任何有限博弈都至少存在一个纳什均衡:不一定是纯策略纳什均衡,例如剪刀-石头-布;寻找博弈的纳什均衡是困难的,至少从算法角度来讲是这样。

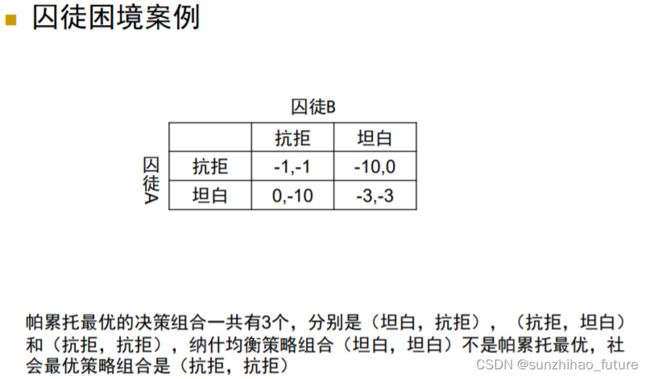
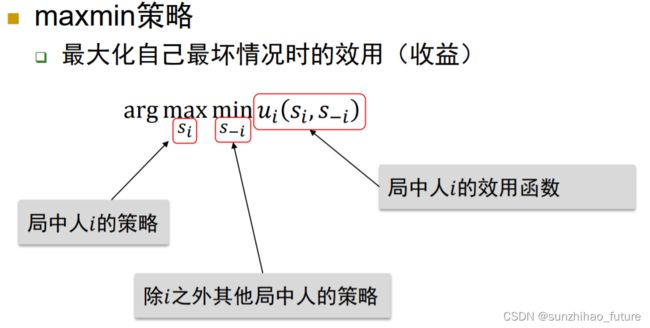
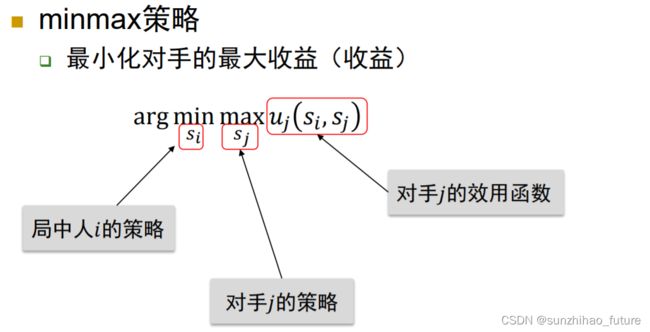
其思想是最小化损失,控制风险;预防其它局中人的不理性给自己带来损失。
田忌赛马
[例题]
田忌和齐王赛马,每人有上、中、下三个等级的马各一匹,上等马优于中等马,中等马优于下等马,同一等级的马中齐王的马优于田忌的马. 比赛共进行三局,每局的胜者得1 分,负者的-1分,比赛结果为三局得分之和。
(1) 请写出田忌赛马这场博弈中的局中人、策略集合和效用矩阵。
(2) 请给出田忌赛马的任意一种混合策略纳什均衡解,并计算此时双方的期望得分。