机器学习__04__朴素贝叶斯算法

朴素贝叶斯

历史解读：

​   18世纪英国业余数学家托马斯·贝叶斯(Thomas Bayes，1702～1761)提出过一种看似显而易见的观点：

​   “用客观的新信息更新我们最初关于某个事物的信念后，我们就会得到一个新的、改进了的信念。”

​   这个研究成果由于简单显得平淡无奇，直至他死后两年才于1763年由他的朋友理查德·普莱斯帮助发表。它的数学原理很容易理解，简单说就是，如果你看到一个人总是做一些好事，则会推断那个人多半会是一个好人。这就是说，当你不能准确知悉一个事物的本质时，你可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。

​   用数学语言表达就是：支持某项属性的事件发生得愈多，则该属性成立的可能性就愈大。

​   与其他统计学方法不同，贝叶斯方法建立在主观判断的基础上，你可以先估计一个值，然后根据客观事实不断修正。

​   1774年，法国数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace，1749-1827)独立地再次发现了贝叶斯公式。拉普拉斯关心的问题是：当存在着大量数据，但数据又可能有各种各样的错误和遗漏的时候，我们如何才能从中找到真实的规律。拉普拉斯研究了男孩和女孩的生育比例。有人观察到，似乎男孩的出生数量比女孩更高。

这一假说到底成立不成立呢?

​   拉普拉斯不断地搜集新增的出生记录，并用之推断原有的概率是否准确。每一个新的记录都减少了不确定性的范围。拉普拉斯给出了我们现在所用的贝叶斯公式的表达：

​ P(A/B)=P(B/A)∗P(A)/P(B)

​   该公式表示在B事件发生的条件下A事件发生的条件概率，等于A事件发生条件下B事件发生的条件概率乘以A事件的概率，再除以B事件发生的概率。公式中，P(A)也叫做先验概率，P(A/B)叫做后验概率。严格地讲，贝叶斯公式至少应被称为“贝叶斯-拉普拉斯公式”。

1.0 概述

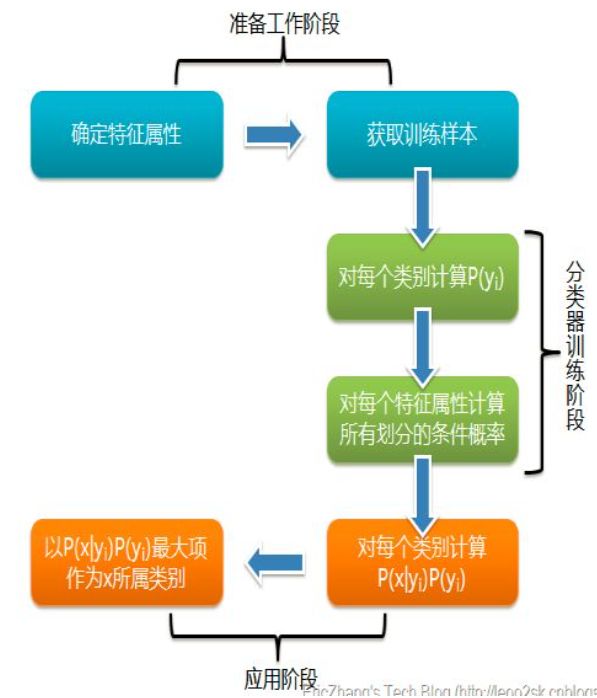
​   朴素贝叶斯是一个基于贝叶斯定理和特征条件独立假设的分类的方法，属于生成模型。朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法。

​   朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素。朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。举个例子，如果一种水果其具有红，圆，直径大概3英寸等特征，该水果可以被判定为是苹果。尽管这些特征相互依赖或者有些特征由其他特征决定，然而朴素贝叶斯分类器认为这些属性在判定该水果是否为苹果的概率分布上独立的。对于某些类型的概率模型，在监督式学习的样本集中能获取得非常好的分类效果。在许多实际应用中，朴素贝叶斯模型参数估计使用最大似然估计方法；换而言之，在不用到贝叶斯概率贝叶斯概率或者任何贝叶斯模型的情况下，朴素贝叶斯模型也能奏效

2.0 相关原理

• P(B|A) 为在事件 A 发生的条件下事件 B 发生的概率（条件概率）
• P(A|B) 为在事件 B 发生的条件下事件 A 发生的概率（条件概率）
• P(A, B) 是事件 A 和事件 B 都发生的概率（联合概率）
• P(B) 和 P(A) 分别是事件 B 和事件 A 发生的概率（边缘概率

贝叶斯公式告诉我们，通过事件 A 的概率，事件 B 的概率和在 B 的情况下事件 A 的概率，可以求得在 A 的情况下事件 B 的概率。

2.1后验概率最大化含义

​   朴素贝叶斯最大化后验概率其实相当于最小期望风险原则，这进一步验证了朴素贝叶斯方法的合理性。

2.2拉普拉斯平滑

​    零概率问题：在计算事件的概率时，如果某个事件在观察样本库（训练集）中没有出现过，会导致该事件的概率结果是0。这是不合理的，不能因为一个事件没有观察到，就被认为该事件一定不可能发生（即该事件的概率为0）。

​    拉普拉斯平滑(Laplacian smoothing) 是为了解决零概率的问题。

​   法国数学家 拉普拉斯 最早提出用 加1 的方法，估计没有出现过的现象的概率。
​ 理论假设：假定训练样本很大时，每个分量x的计数加1造成的估计概率变化可以忽略不计，但可以方便有效的避免零概率问题

​   假设在文本分类中，有3个类：C1、C2、C3。
​ 在指定的训练样本中，某个词语K1，在各个类中观测计数分别为0，990，10。
​ 则对应K1的概率为0，0.99，0.01。

​ 显然C1类中概率为0，不符合实际。

​ 于是对这三个量使用拉普拉斯平滑的计算方法如下：
　　1/1003 = 0.001，991/1003=0.988，11/1003=0.011
​ 在实际的使用中也经常使用加 λ（0≤λ≤1）来代替简单加1。如果对N个计数都加上λ，这时分母也要记得加上N*λ

3.0 朴素贝叶斯的三种形式和实现

3.1高斯型

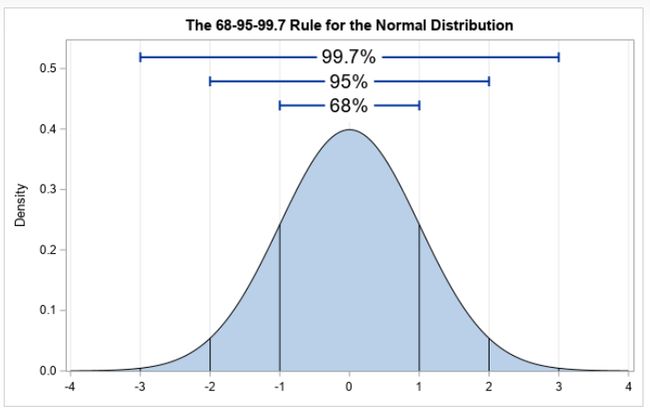
高斯型朴素贝叶斯分类器假设特征的条件概率服从高斯分布

高斯分布(Gaussian Distribution)又称正态分布(Normal Distribution)。

scikit–learn实现如下：

class.sklearn.naive_bayes.GaussianNB()

高斯型朴素贝叶斯分类器没有输入参数。

属性:

​ class_prior_：数组形式，存放训练集数据中各个类别的概率。

​ class_count_:数组形式，存放训练集数据中各个类别包含的训练样本数目

​ theta：各个类别上各个特征的均值。

​ sigma_：各个类别上各个特征的标准差。

方法:

​ fit(X train,y_train):在训练集(X train,.y train)上训练模型。

​ partial_fit((X_train,y_train):当训练数据集规模较大时，可以将其划分为多个小数据集，然后在这些小数据集上连续调用该方法来多次训练模型。

​ score(X_test,y_test):返回模型在测试集(X_test,y_test0)上的预测准确率。

​ predict(X)：用训练好的模型来预测待预测数据集X,返回数据为预测集对应的结果标签y。

​ predict proba(X:返回一个数组，数组的元素依次是预测集X属于各个类别的概率。

​ predict_log_proba(X):返回一个数组，数组的元素依次是预测集X属于各个类别的对数概率。

3.2多项式型

多项式型朴素贝叶斯分类器假设特征的条件概率分步满足多项式分布

​ 多项式分布（Multinomial Distribution）是二项式分布的推广。二项分布的典型例子是扔硬币，硬币正面朝上概率为p, 重复扔n次硬币，k次为正面的概率即为一个二项分布概率。把二项分布公式推广至多种状态，就得到了多项分布。

​ 与高斯型朴素贝叶斯分类器不同，多项式型只适合处理离散特征的情况

scikit-leam实现如下：

class sklearn.naive_bayes.MultinomialNB(alpha=0.01,fit prior=True)

参数:

alpha:指定平滑因子a的值，如a=0.01。

fit_prior:指定是否计算P(Y=ck),默认为True,表示不计算P(Y=cx),而直接用均匀分布代替；如果为False,则表示计算实际的P(Y=ck)。

属性:

class count:数组形式，存放训练集数据中各个类别包含的训练样本数目。

feature_count：数组形式，存放训练集数据中各个特征包含的训练样本数目。

方法与高斯型相同，不再赘述。

3.3伯努利型

伯努利型朴素贝叶斯分类器假设特征的条件概率分步满足二项分布

​ 伯努利分布指的是对于随机变量X有, 参数为p(0是N=1时二项分布的特殊情况。

scikit-leam实现如下：

class sklearn.naive bayes.BernoulliNB(alpha=0.01,binarize=0.0,fit_prior=True)

参数
**alpha:**指定平滑因子α的值，如=0.01。

**binarize:**默认为一个浮点数0.0，表示以该数值为界，将特征取值大于它的编码为1，小于它的编码为0，从而实现对数据集的二值化。当使用binarize=-None时，

​ 模型会假定你已经先将数据集二值化了。

**fit_prior:**指定是否计算P(Y=ck),默认为True,表示不计算P(Y=ck),而直接用均匀分布代替：如果为False,则表示计算实际的P(Y=ck)。

​ 属性与多项式型相同，不再赘述。

​ 方法与高斯型相同，不再赘述。

4.0 中文文本分类项目

4.1项目简介

​ 中文文本分类是文本处理中的一个基本问题，后面涉及的文本情感分析，利用文本内容进行用户画像等更高层次的项目都可以转化为一个文本分类项目。

​ 文本分类器有多种方式可以做，既可以是有监督的，又可以是无监督的，本节主要基于朴素贝叶斯模型的中文文本分类器，因此用的是一种有监督的模型

4.2项目过程

第一步：训练集文本预处理

​   通常，我们拿到的文本数据是含有很多噪声的，比如我们用爬虫从网上爬取的文本数据，可能会包含一些 HT肌1L标签和特殊符号等噪声，因此一般在进行分词之前，需要对其进行预处理。由于本节主要目标是讲解用朴素贝叶斯做文本分类项目的整个过程，因此暂时不考虑数据预处理的事情 ，后期的 综合项目中我们再来详细讲解 。这里先使用别人已经处理好的训练集语料库。

​   网上比较好的中文文本分类语料是搜狗新闻分类语料库，但是因完整版数据量过大，所以这里使用"复旦大学计算机信息与技术系国际数据库中心自然语言处理小组"提供的小样本中文文本分类语料，语料包和程序可直接在本书相关的 GitHub上下载

第二步：中文文本分词

import jieba

content = "中文文本分类是文本处理中的一个基本问题。"

seg_list1 = jieba.cut(content, cut_all=False)
print("默认切分模式")
print(" ".join(seg_list1))

seg_list2 = jieba.cut(content, cut_all=True)
print("全切分模式")
print(" ".join(seg_list2))

seg_list3 = jieba.cut_for_search(content)
print("搜索引擎分词模式")
print(" ".join(seg_list3))

  实际应用中可根据具体的业务情况选择分词模式，本书涉及的分词，采用的都是默认切分模式

第三步：统计文本词频并计算TF-IDF

​    通过分词后的结果，对文本中的单词进行词频统计。

​    如果将文本看做一个对象，那么分词结果就是这个对象的特征，某个词的词频数量越大，说明这个特征越具有代表性（简单理解）。
​    但是你可能会问，像“的”，“是”，这样的常用词哪里具有代表性？
​    因此，我们需要降低这类普遍出现具有较低意义的词的特殊性，这类词的特性就是在大量的文本集合中都有出现，不论是这类文本具有什么样的主题。
​    TF-IDF值就是针对这一问题进行词频统计的。
​    TF是指某一给定词语该文档中的出现次数。
​    IDF是指含有某一指定词在文档集合中出现的次数的倒数再取对数，越多的文档包含该词，值越接近0。
​    TF-IDF值就是 TF*IDF。

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
# 分类好的语料
corpus = ["中文 文本 分类 是 自然语言 处理 中 的 一个 基本 问题",
          "我 爱 自然语言 处理",
          "这 是 一个 问题 以前 我 从来 没有 遇到 过"]
# 词频统计
vectorizer = CountVectorizer()
# 计算TF-IDF
transformer = TfidfTransformer()

tfidf = transformer.fit_transform(vectorizer.fit_transform(corpus))

word = vectorizer.get_feature_names()
for i in word:
    print(i)

weight = tfidf.toarray()
print(weight)

for i in range(len(weight)):
    print("第{}篇文档的词语TF-IDF权重：".format(i))
    for j in range(len(word)):
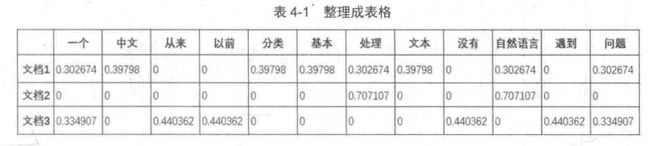
        print(word[j]+":"+str(weight[i][j]))

​    从表中可以清晰地看出整个训练集词袋中所包含的词语情况及其所对应的TF-IDF 值，后期的模型训练就是基于这一文档的 TF-ID 矩阵来进行的。

python 的 sklearn 工具提供了各种模型，包括了朴素贝叶斯模型：

#这里是假设有训练文本和对应的类别标签的代码,仅供参考，无法运行
from sklearn.cross_validation import train_test_split
# 数据集7/3分
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
from sklearn.naive_bayes import MultinomialNB
from sklearn import metrics
# 训练
bayes_clf = MultinomialNB(alpha=0.01,fit_prior=True)
bayes_clf.fit(X_train,y_train)
# 预测
y_pred = bayes_clf.predict(X_test)
y_predprob = bayes_clf.predict_proba(X_test)[:,1]
# 测试集验证模型
precision = metrics.precision_score(y_test,y_pred)
recall = metrics.recall_score(y_test,y_pred)
F1 = metrics.f1_score(y_test,y_pred)
# 交叉验证
from sklearn.cross_validation import cross_val_score
cross_result = cross_val_score(bayes_clf,X_test,y_test,cv=5)

print("模型在测试集上的预测情况如下：")
print("准确率：%0.6f".format(cross_result))
print("查全率：%0.6f".format(precision))
print("查准率：%0.6f".format(recall))
print("F1值：%0.6f".format(F1))

4.3完整程序实现

这里我们使用复旦大学的语料包进行一次分析和预测

# coding = utf-8
import os
import jieba
from numpy.lib.function_base import vectorize

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import cross_val_score
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix


def readfile(path):
    with open(path, 'r', encoding='utf8', errors="ignore") as f:
        return f.read()


def processData(corpus_path):
    train_corpus = []
    train_label = []
    cate_list = os.listdir(corpus_path)
    for mydir in cate_list:
        class_path = corpus_path + mydir + "/"
        file_list = os.listdir(class_path)
        for file_path in file_list:
            fullname = class_path + file_path
            content = readfile(fullname)
            # 对文本进行处理
            content.strip()
            content.replace('\r\n', '').strip()
            content_seg = jieba.cut(content)
            train_corpus.append(" ".join(content_seg))
            train_label.append(mydir)
    print("分词结束...")
    return train_corpus, train_label


def train(train_corpus, train_label, stpwrdlst):
    vectorizer = CountVectorizer(stop_words=stpwrdlst, max_df=0.5)
    transformer = TfidfTransformer()
    tfidf = transformer.fit_transform(vectorizer.fit_transform(train_corpus))
    weight = tfidf.toarray()
    print(weight)
    print("生成TF-IDF矩阵结束...")

    # 7/3分划分为训练集和验证集
    X_train, X_test, y_train, y_test = train_test_split(tfidf, train_label, test_size=0.3)
    # 训练
    bayse_clf = MultinomialNB(alpha=0.01, fit_prior=True)
    bayse_clf.fit(X_train, y_train)
    print("模型训练结束...")
    print("在验证集上的预测情况如下：")
    y_pred = bayse_clf.predict(X_test)
    print("交叉验证：")
    print(cross_val_score(bayse_clf, X_test, y_test, cv=5))
    print(classification_report(y_test, y_pred, target_names=None))
    print("混淆矩阵：")
    print(confusion_matrix(y_test, y_pred))


if __name__ == "__main__":
    # 数据处理
    corpus_path = "中文文本分类项目数据集/train_corpus/"
    train_corpus, train_label = processData(corpus_path)
    # 读取停用词
    stopword_path = "中文文本分类项目数据集/hlt_stop_words.txt"
    stpwrdlst = readfile(stopword_path).splitlines()
    # 开始训练
    train(train_corpus, train_label, stpwrdlst)