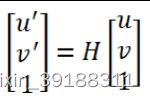基于机器学习的视频防抖处理

视频防抖动

一、图像质量评估指标PSNR和SSIM

PSNR（Peak Signal-to-Noise Ratio）峰值信噪比

定义原始图像（干净图像）I和噪声图像K,则有

---

二、Hybrid Neural Fusion for Full-frame Video Stabilization用于全帧视频稳定的混合神经融合

---

三、Deep Online Fused Video Stablization 深度在线融合视频稳定

gyroscope陀螺仪

• 放在前面的知识

  • 什么是陀螺仪？
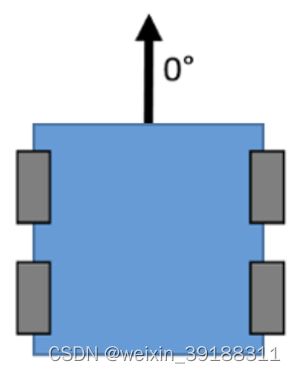
    陀螺仪说白了就是指示角度偏移的传感器，一般在机器人等设备中处于核心传感器，每一个陀螺仪均在每一秒产生一个输出，单位就是度/秒，表示特定时间内旋转速率的度量，度量越大代表机器人的旋转越快，机器人不会每一秒就输出一个旋转度数，而是输出一段时间内的数百个读数，计算得到角度变化，如下图所示：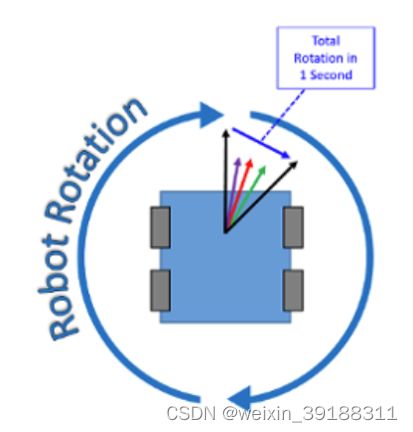

  而机器人通电启动时候放置的方向将作为0度，如下图所示：
  

  随着时间的推移，机器人将会获得一个实际的偏移角度，对这种漂移影响最大的因素是陀螺仪的偏置稳定度规格，这是衡量陀螺仪在长时间段内测量结果稳定性的一个指标。如果将机器人开启一个小时并且不移动它，陀螺仪在一个小时结束时读取的数值就不是零。也就是说如果开电一个小时，机器人放置静止，一个小时后可能机器人会产生20-30度的偏转角度，而开电十分钟之内可能会产生3度左右的偏转，这些偏移角度都将是机器人前进方向相比较之前产生的偏转。这就是陀螺仪的漂移。

• 陀螺仪数据校准

  零点偏移量，这个概念主要是飞控中对陀螺仪进行数据的校准必须掌握的概念。什么叫陀螺仪的数据校准：飞控所获得的数据减去零点偏移量集可，而零点偏移量就是采集到的数据的平均值。

• 陀螺仪数据校准的目的

  根据陀螺仪计算得到的零点偏差对于水平稳定有着重要的作用，例如X轴产生0.2度/秒的零偏，那么通过X轴计算得到的角度也不会从0度开始，直接会导致姿态角产生一定的偏差，飞行过程中会很难控制水平。

• 校准方法

  上电会自动校准，产生零偏，每次上电得到的零偏量是不同的。

  注意 陀螺仪上电校准需要静止一段时间，否则是一段错误的数值，这是因为陀螺仪的校准需要识别静止状态（两次采集到的数据差的和是否超过阈值，超过阈值则说明处于运动状态），否则代码将一直处于待机循环状态直至静止状态符合。

• 陀螺仪的误差分析
  误差主要是两类:

  • 系统性误差

    本质上就是有规律的误差，可以实时补偿，常值偏移、轴安装误差、比例因子等

  • 随机误差

    本质上就是随机产生的噪声，一般情况下比较难拟合，没有固定的函数去拟合产生的噪声项，一般采用时间分析法对误差进行建模分析，再通过卡尔曼滤波等算法去减小噪声项的影响。（注卡尔曼滤波，也就是通过前一时刻以及以往产生的误差来预计下一时刻物体的最佳位置或者可能出现位置）

• 从物理意义以及误差来源可以将误差分为如下几种陀螺仪的误差：

  • 常值漂移 ： 长时间不随时间变化的测试数据的均值（0偏移量）
  • 角度随机游走（Angle Rate Random Walk, ARRW）: 光学陀螺具有速率积分的特性，由角速率随机白噪声积分引起的误差角增量具有随机游动的特性，这一误差被称为光学陀螺的角度随机游走(陀螺角随机游走（Angular Random Walk）是表征陀螺仪角速度输出白噪声大小的一项技术指标，ARW)。 这一误差的主要来源是：光子的自发辐射、探测器的散粒噪声、机械抖动；另外，其它相关时间比采样时间短得多的高频噪声，也引起光学陀螺的角度随机游走。对于采用抖动偏频的激光陀螺来说，由于交变偏频使激光陀螺频繁通过锁区，产生较大的角度随机游走误差，该误差成为激光陀螺的主要误差源。 角度随机游走噪声的带宽一般低于10Hz，处于大多数姿态控制系统的带宽之内。因此，若不能精确确定角度随机游走，它有可能成为限制姿态控制系统精度的主要误差源。
  • 速率随机游走
  • 量化噪声
  • 速率斜坡

---

四、图像防抖的算法本质

1. $运动分析$，视频抖动的本质是图像存在着微小、方向随机、频率较高的运动。首先要检测到图像帧与帧之间的运动方向

2. $角点预测$，图像中的任何一个物体都通常含有独特的特征，但往往由大量的像素点构成。角点是能够准确描述这个物体的一个数量较少的点集。角点检测算法可以分析出图像最明显的特征点，用于物件识别和跟踪。

3. $光流/opticalflow$, 由于目标对象或者摄像机的移动造成的图像对象在连续两帧图像中的移动被称为光流。它是一个2D向量场，可以用来显示一个点从第一帧图像到第二帧图像之间的移动。

4. $RANSAC/随机数一致$, 它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数。两帧连续图像有各自的角点集合，RANSAC可以从含有噪声的数据中发现相互匹配的点集，进而计算出两帧图像的变换矩阵。

5. $运动平滑$

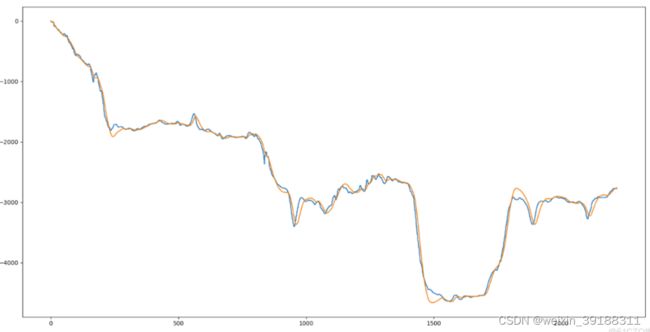
5.1 $维度选择$ **利用图像匹配算法，我们可以获得两幅图像之间的变换矩阵，矩阵包含了大量的信息。但在视频防抖需求中，我们需要关心的只有3个信息：水平位移、竖直位移和旋转角度。从矩阵中抽出相应的值，可以得到如下运动轨迹曲线。曲线中大量的“毛刺”就是我们要消除的抖动：

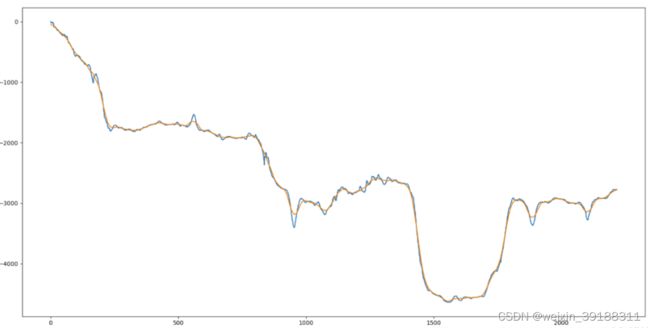
5.2 $轨迹平滑$。 这里一般使用滤波、拟合或最优化等方法来对曲线进行平滑

5.2.1 $卡尔曼滤波$，Kalman滤波在控制类场景中运用较多，使用前面的运动来预测下一个运动，消除采样噪声。由于Kalman只依赖前面的数据，所以更适合$\text{软件实时防抖}$。在后期防抖中，得出的结果往往会有一些“惯性”，效果并非最佳。

5.2.2 $中值滤波$，一种最简单但有效的滤波方式。在防抖场景中的缺点是对结果缺乏掌控。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3H998oYw-1662002826701)(./images/中值.png)]

5.3 $修复运动计算$。 平滑轨迹与原始轨迹做差即可获得修复运动参数。

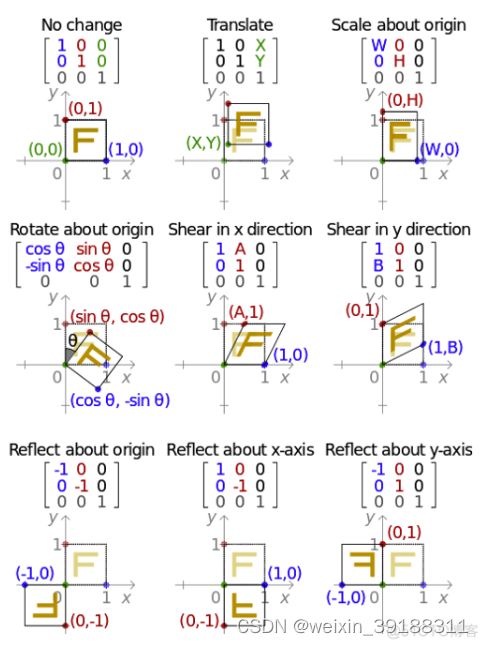
6. $图像变换$，$\text{仿射变换}$（Affine Transformation或 Affine Map）是一种二维坐标到二维坐标之间的线性变换，它可以保持图像的平直性和平行性。变换方式与矩阵参数的一些基本形式如下图。

---

五、MeshFlow: Minimum Latency Online Video Stabilization 最小延迟在线视频稳定

本质上是$\text{图像对齐}$的任务。视频稳定通过两种方式，离线和在线，离线方式就是诸如premire类似的后处理工具；在线视频稳定通过两种方式：单一运动参数模型（仿射、单适应性等）或者陀螺仪传感器。meshflow是一个空间平滑稀疏运动场，空间矢量只存在于空间网格的顶点，特别是，匹配特征点上的运动矢量被转移到其相应的附近网格顶点。网格流是通过两个中值滤波器为每个顶点指定一个唯一的运动矢量来生成的。
MeshFlow方法可以概括如下：在视频帧上放置一个规则的2D网格。我们会跟踪连续帧之间的图像特征角点，在每个特征角点位置处会生成一个运动矢量。接下来，将这些运动矢量转移到其相应的附近网格顶点，以便每个顶点从其周围特征累积若干运动。meshflow是由所有网格顶点运动组成的一个稀疏2D阵列

5.1 MeshFlow获取

(1) $网格$。首先在每一帧的图像上形成16x16的网格

(2) $获取motionvector(MV)$。特征提取图像，一般是获取到图像的特征角点集合（通过具体的方法函数获得FAST或者SIFT或者ORB特征角点集合），相邻帧匹配到的特征位置的差作为MV，特征差也就是运动矢量，反映后面的帧在前一帧上面的运动趋势。针对一对特征匹配点$P$和$\hat{P}$，有运动矢量$V_P=P-\hat{P}$

(3) $得到MeshFlow$，将MV关联到相邻的网格顶点，可以在下图中看出，$p$点以及$p^{\prime }$分别表示当前帧以及上一帧上的某一个图像特征点位置，然后在当前帧上形成了16 $\times$ 16的网格，进一步在当前特征点所在的位置上形成一个椭圆区域，该区域包含了n个网格区域，将每一个网格区域的顶点均赋予特征点所在的运动矢量。

下述的流程表示了上述的三个步骤:

(4) $第一个中值滤波器F1进行过滤$。一个网格顶点会关联到多个特征匹配的MV，用F1进行平滑处理得到规则化的meshflow。如图所示：

(5) $第二个中值滤波器F2进行过滤$。在3 $\times$ 3的中值滤波器处理之后，去除离群点噪声，产生空间稀疏运动场。$黄色箭头$就是噪声流，而$橙色箭头$则是我们想要的网格顶点流，如图所示：

两个中值滤波器提供了必要的空间平滑，对于噪声流也就是不一致流的处理至关重要，噪声流上的运动补偿一般会造成空间视觉中不连续边界的渲染虚伪影，

(6) $顶点profile$。每一个顶点MV路径内数据。

5.2 鲁棒估计

每一个网格产生多个MV，而角点响应了全局阈值的大小，阈值容易受到高纹理区域的偏移，因此，全局角点响应阈值->划分为小区域的局部响应阈值，旨在避免在语义信息少的区域（纹理较差的区域）采集不到MV，例如天空地面就很容易采集不到MV。根据网格划分，设置局部阈值，避免部分网格内检测不到合适数量的特征点的问题。

5.3 去除异常值 $

原图划分为4x4的子图，使用局部RANSAC排除离群点。由误匹配和动态目标产生的运动背离可以被成功去除，由深度变化和镜头rolling影响产生的小变化点可以被保留。中值滤波和RANSAC都对鲁棒的去处离群点很重要，前者局部作用，后者在更全局的范围作用。

5.4 pre-warping

在MehFlow之前，用全部匹配后的特征点计算出一个全局的单应性矩阵$F_t$用以表征全图的运动向量$V_t$，并用$F_t$对$\hat{P}$的坐标进行预矫正，即该点的局部运动向量为$\widehat{V_P}=P-F_t\hat{P}$，该点的全部运动向量为$V_P=V_t+\widehat{V_P}$。warping 操作得到最后组合的全局和局部的组合图像帧。

计算一个基准速度

5.5 PAPS（Predicted Adaptive Path Smoothing）

5.5.1 离线自适应性平滑

$\mathcal{O}(\mathbf{P}(t))={\sum }_t\left(\Vert \mathbf{P}(t)-\mathbf{C}(t){\Vert }^2+{\lambda }_t{\sum }_{r\in {\Omega }_t}{w}_{t,r}\Vert \mathbf{P}(t)-\mathbf{P}(r){\Vert }^2\right)$

上述的等式中，$\mathbf{P}(t)$是优化路径，而$\mathbf{C}(t)$则是原始路径，${\lambda }_t$是平衡参数也是最重要的参数，它如果值为0，表示视频帧没有发生任何的裁剪和抖动，因此设置它的值越小表示视频帧的裁剪和抖动程度将会越少。${\omega }_t$是时序半径，$w_{t,r}$是高斯分布权重。前项约束优化path与原始path一致，后项约束序列窗口之间每一帧的平滑，离线场景依赖前后帧，每一帧求解一个最优解${\lambda }_t$。

5.5.2 预测${\lambda }_t$。

使用离线视频，预测出场景下适用的λt。使用两个相关标志元素，转移元素Tv（适合快速镜头移动），仿射组成元素Fa（适合复杂景深变换），两个都从相邻帧的全局homography中提取。其中，Tv转移元素的计算方式是计算前后帧之间的移，计算方式如下：

$T_v=\sqrt{\left(v_x^2+v_y^2\right)}$

Fa由homography中两个最大的特征值比值计算。视频数据集离线优化，拟合与λt线性关系：

${\lambda }_t^{\prime }=-1.93\ast T_v+0.95$

${\lambda }_t^{\prime \prime }=5.83\ast F_a+4.88$

最终的${\lambda }_t$通过$max(min({\lambda }_t\prime ,{\lambda }_t\prime \prime ),0)$取得，越小的${\lambda }_t$越可以拟合两者，

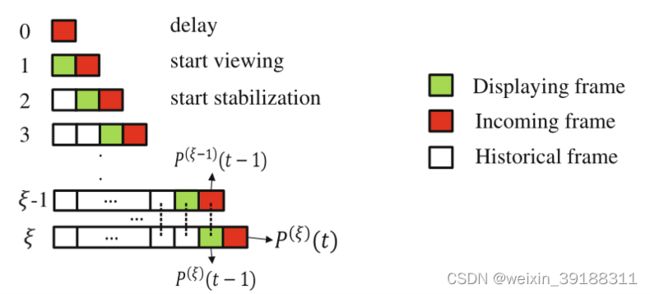
5.5.3 在线平滑处理

下图展示的是我们可视化在线视频稳定的一个流程直观图：

其中，红色的是未来帧，会在初始的时候延迟一帧的间隔，而绿色是展示的我们所看到的视频帧，白色的是过去帧。
采用一个移动的缓存窗口用来缓存过去帧，丢弃最旧的视频帧保留较新的视频帧，这个buffer初始设置很小并逐步增加大小。
40帧前向缓存buffer，增加第三项约束
$\begin{array}{rl}\mathcal{O}({\mathbf{P}}^{(\xi )}(t))& =\sum _{t\in \Phi }(\Vert {\mathbf{P}}^{(\xi )}(t)-\mathbf{C}(t){\Vert }^2+{\lambda }_t\sum _{t\in \Phi ,r\in {\Omega }_t}{w}_{t,r}\Vert {\mathbf{P}}^{(\xi )}(t)-{\mathbf{P}}^{(\xi )}(r){\Vert }^2)\\ & +\beta \sum _{t\in \Phi }\Vert {\mathbf{P}}^{(\xi )}(t-1)-{\mathbf{P}}^{(\xi -1)}(t-1){\Vert }^2\end{array}$

5.6 视觉修复

U = P-C

优化网格顶点运动P减去原始网格顶点运动C，得到更新运动向量U，也就是更新运动网格。依据更新运动网格对原图warp

六、 评估指标

三项评估指标越接近于1说明效果越好

6.1 裁剪比（cropping ratio）

去掉黑色边界区域之后的视频图像比例，比例越大说明裁剪越少，视频的质量效果越好。在输入和输出视频之间的每一帧处都安装了单应性Bt。每个帧的裁剪比可以从单应性的比例分量中提取。我们对所有帧的所有比率进行平均，以得出裁剪比率。

6.2 失真得分（distortion score）

该项指标同样由Bt产生，Bt中的两项最大的特征值比值作为失真得分的估计，该比值同样作为了求平衡参数时候的Fa的计算方式。每一个帧都会产生一个失真得分，选择最差的作为最终的失真得分

6.3 稳定性分数（stability score）

我们使用从稳定视频中提取的顶点轮廓进行评估。我们在频域中分析每个顶点轮廓。我们取几个最低频率的结果并计算全频率上的能量百分比（直流分量除外）。从所有配置文件中取平均值得出最终分数

6.3

七、图像对齐

7.1 图像对齐的步骤

对于两个图像A和B，首先提起各自的图像特征，然后匹配A与B图像中的特征，然后求解A与B的对齐矩阵，这个对齐矩阵就是求变换矩阵的过程，之前是最小二乘法现在是随机数一致方法，其基本思想如图：

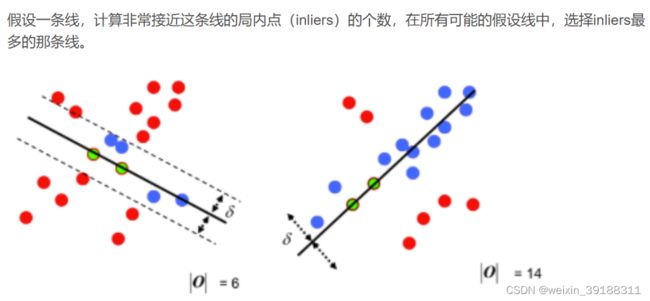
即————随机选取S个样本点，生成一个模型，这个模型会对对这些样本点的局内点进行计数，重复N次之后选取样本点最多的模型

八、透视变换（homograpgy）

homography也被称为H矩阵 它就是一个3 $\times$ 3的矩阵，一般使用单应性矩阵关联同一个场景下的两个图片，从而实现全景拼接。如图

具体有如下不同2D仿射变换类型：

• 投影变换8dof —将图像转换为不同的投影。

• 仿射变换6dof —转换将保留原图像平行线的图像。

• 欧几里得变换3dof —旋转原图像。

• 相似变换4dof —旋转和缩放原图像

我们用下图中的公式表示仿射变换，

也就是$X^{\prime }=H(X)$，而原始图像就是$X$，变换后的图像就是$X^{\prime }$

$\text{注意}$

利用单应性矩阵做图像拼接的时候，如果只在二维的空间中处理，要求相机的中心不能有$平移$，因为这样可以在不知道场景深度信息的条件下就可以完成图像的拼接;有一种情况，就算相机中心有移动，也可以利用单应性矩阵对图像拼接。就是拍摄的场景是平面的时候。
下面先尝试着理解下面的式子，这个是单应性矩阵的完整定义：
$\mathbf{H}⟹\{\mathbf{R},\mathbf{t},\mathbf{n}\}$
，其中R是旋转矩阵，t是平移矩阵，n是法向量

$H=s\left[\begin{array}{ccc}{f}_x& \gamma & u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{lll}{r}_1& r_2& t\end{array}\right]=sM\left[\begin{array}{lll}{r}_1& r_2& t\end{array}\right]$

即

$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=s\left[\begin{array}{ccc}{f}_x& \gamma & u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{lll}{r}_1& r_2& t\end{array}\right]\left[\begin{array}{c}{x}_W\\ y_W\\ 1\end{array}\right]$，其中，$M=\left[\begin{array}{ccc}{f}_x& \gamma & u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]$ 表示内参矩阵

我们定义如下：u和v分别是转换之后的坐标，可以表示为(u,v)，而s是尺度因子，M中的五个量是相机生产过程中产生的误差，相当于相机内参，通常影响很小，{R,t}则是相机外参，xw和yw分别代表原始图像中的坐标。

下面我们看两个案例巩固H矩阵：H矩阵默认最少是4对匹配点，多则更加准确。
如下是两个图片的放射变换，主要是变换的是球场位置：

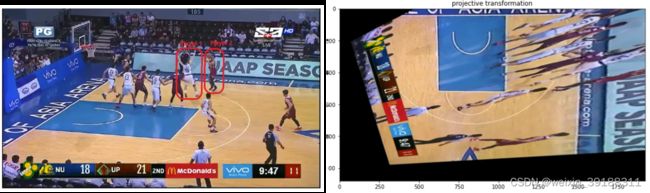
具体的代码实现如下：

import numpy as np
import matplotlib.pyplot as plt
from skimage.io import imread, imshow
from skimage import transform
still1 = imread('still1.png')
src = np.array([(608, 641),
                (683, 553),
                (1841, 678),
                (1750, 579)])
dst = np.array([(800, 339),
                (1273, 339),
                (800, 1000),
                (1310, 1000)])
tform = transform.estimate_transform('projective', src, dst)
tf_still1 = transform.warp(still1, tform.inverse)
fig, ax = plt.subplots(figsize=(20, 6))
ax.imshow(tf_still1)
ax.set_title('projective transformation')

下面是另一个案例转正比萨斜塔：

tower = imread('tower_pisa.jpeg')
src = np.array([(291, 329),
                (537, 344),
                (230, 868),
                (507, 891)])
dst = np.array([(220, 320),
                (462, 320),
                (220, 870),
                (462, 870)])
tform = transform.estimate_transform('euclidean', src, dst)
tf_still1 = transform.warp(tower, tform.inverse)
fig, (ax0, ax1) = plt.subplots(1, 2, figsize=(12, 8))
ax0.imshow(tower)
ax0.set_title('Leaning tower of Pisa')
ax0.set_axis_off()
ax1.imshow(tf_still1)
ax1.set_title('Euclidean transformation')
ax1.set_axis_off()
plt.tight_layout()

如何找到单应性矩阵（homography）

理论上只要获知大于等于四对匹配的特征点就可以使用opencv中的homography方法——findhomography(),找到图片中的对应关键点或者称之为角点特征可以使用opencv中的sift、surf或者orb，一般sift和surf都是收费的，而orb是免费的

ORB本质是带方向的FAST特征点和BRIEF描述子，其中FAST是定位器，找寻图片中具有图片特征的x和y的坐标；而BRIEF是获取到不同图片同一个位置相同的外观编码

以下是一个具体的案例：

title: 基于特征的图像对齐

content：

1. 读取图片到内存，通过cv.imread()方法或者视频的读取方式
2. 获取检测特征点， 计算两幅图像的orb，一般四个足矣，但是检测方法本身会得到图像上成百上千的特征点，通过MAX_FEATURES控制特征点的数量，通过detectandcompute函数得到特征点并进行描述子的计算
3. 特征匹配，有了描述子计算得到了诸多的外观编码，接下来对诸多特征编码进行匹配，可以通过汉明距离等方式度量特征点之间的相似程度，一次找到两图中匹配的特征点，并按照匹配程度进行排列，保留最匹配的小部分，并将匹配的特征点画出来（可能只有20%-30%是匹配正确的）
4. 计算单应性矩阵，基于匹配得到的特征点，里面虽然有大量的误差以及噪声，但是依然通过findHomography()函数中的随机数一致得到H矩阵或者叫做变换矩阵，随机数一致本身就可以在大量错误存在的情况下得到单应性矩阵。
5. 扭转图片，通过warpperspective函数进行图像对应像素的扭转操作等完成最终的图像的对齐

from __future__ import print_function
import cv2
import numpy as np


MAX_FEATURES = 500 #定义最大匹配的特征检测点的数量，这里定义500
GOOD_MATCH_PERCENT = 0.15 #定义保留15%的存好率

#返回图像和h矩阵
def alignImages(im1, im2):

  # 转换图像为灰度图像
  im1Gray = cv2.cvtColor(im1, cv2.COLOR_BGR2GRAY)
  im2Gray = cv2.cvtColor(im2, cv2.COLOR_BGR2GRAY)

  # ORB计算FAST和BRIEF
  orb = cv2.ORB_create(MAX_FEATURES)
  # 得到两幅图像的两组FAST和BRIEF
  keypoints1, descriptors1 = orb.detectAndCompute(im1Gray, None) 
  keypoints2, descriptors2 = orb.detectAndCompute(im2Gray, None)

  # 匹配特征，方法通过汉明距离进行检测匹配，首先定义一个检测器，然后使用这个检测器对具体的两幅图像进行匹配
  matcher = cv2.DescriptorMatcher_create(cv2.DESCRIPTOR_MATCHER_BRUTEFORCE_HAMMING)
  matches = matcher.match(descriptors1, descriptors2, None)

  # 按照匹配度排序
  matches.sort(key=lambda x: x.distance, reverse=False)

  # 去除匹配度不好的组合，保留较好的组合
  numGoodMatches = int(len(matches) * GOOD_MATCH_PERCENT)
  matches = matches[:numGoodMatches]

  # 画包含有匹配线条的图像，这一步可有可无
  imMatches = cv2.drawMatches(im1, keypoints1, im2, keypoints2, matches, None)
  cv2.imwrite("matches.jpg", imMatches)

  # 提取匹配组合的位置，这里相当于定于了n行2列的坐标
  points1 = np.zeros((len(matches), 2), dtype=np.float32)
  points2 = np.zeros((len(matches), 2), dtype=np.float32)

#查找单应性矩阵并给予坐标的匹配
  for i, match in enumerate(matches):
    points1[i, :] = keypoints1[match.queryIdx].pt
    points2[i, :] = keypoints2[match.trainIdx].pt

  # 使用homography方法得到h矩阵
  h, mask = cv2.findHomography(points1, points2, cv2.RANSAC)

  # Use homography
  height, width, channels = im2.shape
  im1Reg = cv2.warpPerspective(im1, h, (width, height))

  return im1Reg, h


if __name__ == '__main__':

  # Read reference image
  refFilename = "form.jpg"
  print("Reading reference image : ", refFilename)
  imReference = cv2.imread(refFilename, cv2.IMREAD_COLOR)

  # Read image to be aligned
  imFilename = "scanned-form.jpg"
  print("Reading image to align : ", imFilename);  
  im = cv2.imread(imFilename, cv2.IMREAD_COLOR)

  print("Aligning images ...")
  # Registered image will be resotred in imReg. 
  # The estimated homography will be stored in h. 
  imReg, h = alignImages(im, imReference)

  # Write aligned image to disk. 
  outFilename = "aligned.jpg"
  print("Saving aligned image : ", outFilename); 
  cv2.imwrite(outFilename, imReg)

  # Print estimated homography
  print("Estimated homography : \n",  h)

---

另外一个案例的写法：

import os
import cv2
import numpy as np

#读取图片和缩放图片
img1=cv2.imread('images/img1.jpg')
img1=cv2.resize(src=img1,dsize=(450,450))
gray1=cv2.cvtColor(src=img1,code=cv2.COLOR_BGR2GRAY)

img2=cv2.imread('images/img2.jpg')
img2=cv2.resize(src=img2,dsize=(450,450))
gray2=cv2.cvtColor(src=img2,code=cv2.COLOR_BGR2GRAY)

#创建SIFT（老版本中的方法是这么弄，新版本中不是这么弄的）
#sift=cv2.xfeatures2d.SIFT_create()
sift = cv2.SIFT_create()
#计算特征点和描述点
kp1,des1=sift.detectAndCompute(gray1,None)
kp2,des2=sift.detectAndCompute(gray2,None)

#使用KDTREE算法，树的层级使用5
index_params=dict(algorithm=1,trees=5)
search_params=dict(checks=50)
#创建匹配器
flann=cv2.FlannBasedMatcher(index_params,search_params)
#特征点匹配
match=flann.knnMatch(des1,des2,k=2)
print('mathc: {}'.format(match))
#绘制匹配特征点
good=[]
for i ,(m,n) in enumerate(match):
    if m.distance<0.7*n.distance:
        good.append(m)

#当匹配项大于4时
if len(good)>=4:
    #查找单应性矩阵
    srcPoints=np.float32([kp1[m.queryIdx].pt for m in good]).reshape(-1,1,2)#转换为n行的元素，每一行一个元素，并且这个元素由两个值组成
    dstPoints=np.float32([kp2[m.trainIdx].pt for m in good]).reshape(-1,1,2)
    #获取单应性矩阵
    H,_=cv2.findHomography(srcPoints=srcPoints,dstPoints=dstPoints,method=cv2.RANSAC,ransacReprojThreshold=5.0)

    #要搜索的图的四个角点
    h,w=np.shape(img1)[0],np.shape(img1)[1]
    pts=np.float32([[0,0],[0,h-1],[w-1,h-1],[w-1,0]]).reshape(-1,1,2)
    dst=cv2.perspectiveTransform(src=pts,m=H)
    #绘制多边形
    cv2.polylines(img=img2,pts=[np.int32(dst)],isClosed=True,color=(0,255,0))
dest=cv2.drawMatchesKnn(img1=img1,keypoints1=kp1,img2=img2,keypoints2=kp2,matches1to2=[good],outImg=None,matchColor=(0,255,0))
cv2.waitKey(0)
cv2.destroyAllWindows()

if __name__ == '__main__':
    print('Pycharm')

---

OpticalFlow 光流场

光流场反映前一帧和当前帧之间的运动关系，具体就是反映每一个像素点的运动矢量。光流可以分为两种：稠密光流和稀疏光流。

• 稠密光流（图像上所有像素点的光流都计算出来）
  • calcOpticalFlowFarneBack()
  • calcOpticalFlowHS()
  • calcOpticalFlowBM()
  • calcOpticalFlowSF()
• 稀疏光流（计算某些点集的光流）
  • calcOpticalFlowPyrLK()

稠密光流需要使用某种插值方法在比较容易跟踪的像素之间进行插值,从而解决那些运动不明确的像素，所以它的计算开销是相当大的。而对于稀疏光流来说，计算时需要在被跟踪之前指定一组点（容易跟踪的点，例如角点），因此在使用LK方法之前我们需要配合使用cvGoodFeatureToTrack()来寻找角点，然后利用金字塔LK光流算法，对运动进行跟踪。但个人感觉，对于少纹理的目标，例如人手，LK稀疏光流就比较容易跟丢

光流的案例A：

import numpy as np
import cv2
import argparse
parser = argparse.ArgumentParser(description='传入的一段视频的名字为slow_traffic_small.mp4')
parser.add_argument('xxxvideo', type=str, help='path to image file')
args = parser.parse_args()
#opencv中获取视频流的写法
cap = cv2.VideoCapture(args.xxxvideo)
w = int(cap.get(cv2.CAP_PROP_FRAME_WIDTH)) #获取到视频的宽
h = int(cap.get(cv2.CAP_PROP_FRAME_HEIGHT)) #获取到视频的高
writer = cv2.VideoWriter('demo.mp4', cv2.VideoWriter_fourcc(*'mp4v'),
        30, (w, h))
# params for ShiTomasi corner detection
# 定义参数字典
feature_params = dict( maxCorners = 100,
                       qualityLevel = 0.3,
                       minDistance = 7,
                       blockSize = 7 )
# lucas kanade 光流的参数设置
lk_params = dict( winSize  = (15,15),
                  maxLevel = 2,
                  criteria = (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 0.03))
# Create some random colors
color = np.random.randint(0,255,(100,3))
# Take first frame and find corners in it
ret, old_frame = cap.read()
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
#goodfeaturetotrack()函数是用来找到光流估计的角点，参数说明：old_gray表示输入图片，mask表示掩模，feature_params:maxCorners=100角点的最大个数,qualityLevel=0.3角点品质,minDistance=7即在这个范围内只存在一个品质最好的角点
p0 = cv2.goodFeaturesToTrack(old_gray, mask = None, **feature_params)
# Create a mask image for drawing purposes
mask = np.zeros_like(old_frame)
while ret:
    ret, frame = cap.read()
    if not ret:
        break
    frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
    # calculate optical flow
    #参数说明：pl表示光流检测后的角点位置，st表示是否是运动的角点，err表示是否出错，old_gray表示输入前一帧图片，frame_gray表示后一帧图片，p0表示需要检测的角点，lk_params：winSize表示选择多少个点进行u和v的求解，maxLevel表示空间金字塔的层数
    p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)
    # Select good points
    if p1 is not None:
        good_new = p1[st==1]
        good_old = p0[st==1]
    # draw the tracks
    for i,(new,old) in enumerate(zip(good_new, good_old)):
        a,b = new.ravel()
        c,d = old.ravel()
        mask = cv2.line(mask, (int(a),int(b)),(int(c),int(d)), color[i].tolist(), 2)
        frame = cv2.circle(frame,(int(a),int(b)),5,color[i].tolist(),-1)
    img = cv2.add(frame, mask)
    # cv.imshow('frame',img)
    writer.write(img)
    # Now update the previous frame and previous points
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1,1,2)

光流案例B：

import numpy as np
import cv2


# 第一步：视频的读入
cap = cv2.VideoCapture('test.avi')

# 第二步：构建角点检测所需参数
feature_params = dict(maxCorners=100,
                      qualityLevel=0.3,
                      minDistance=7)

# lucas kanade参数
lk_params = dict(winSize=(15, 15),
                 maxLevel=2)

# 随机颜色条
color = np.random.randint(0, 255, (100, 3))

# 第三步：拿到第一帧图像并灰度化作为前一帧图片
ret, old_frame = cap.read()
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
# 第四步:返回所有检测特征点，需要输入图片，角点的最大数量，品质因子，minDistance=7如果这个角点里有比这个强的就不要这个弱的
p0 = cv2.goodFeaturesToTrack(old_gray, mask=None, **feature_params)

# 第五步:创建一个mask, 用于进行横线的绘制
mask = np.zeros_like(old_frame)

while(True):
    # 第六步：读取图片灰度化作为后一张图片的输入
    ret, frame = cap.read()
    frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

    # 第七步：进行光流检测需要输入前一帧和当前图像及前一帧检测到的角点
    pl, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)

    # 第八步：读取运动了的角点st == 1表示检测到的运动物体，即v和u表示为0
    good_new = pl[st==1]
    good_old = p0[st==1]

    # # 第九步：绘制轨迹
    for i, (new, old) in enumerate(zip(good_new, good_old)):
        a, b = new.ravel()
        c, d = old.ravel()
        mask = cv2.line(mask, (a, b), (c, d), color[i].tolist(), 2)
        frame = cv2.circle(frame, (a, b), 5, color[i].tolist(), -1)
    # 第十步：将两个图片进行结合，并进行图片展示
    img = cv2.add(frame, mask)

    cv2.imshow('frame', img)
    k = cv2.waitKey(150) & 0xff
    if k == 27:
        break

    # 第十一步：更新前一帧图片和角点的位置
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1, 1, 2)
    # p0 = cv2.goodFeaturesToTrack(old_gray, mask=None, **feature_params)

cv2.destroyAllWindows()
cap.release()

---

九、Real-time Video Stitching

摘要

核心成分就是两个：一个初始的视频帧间的homography（between-camera，BC），每一帧中都存在的相机路径homography（CP）用于估计BC。BC homography通过使用块匹配来调整估计CP的误差来细化（单应性细化）。为了快速处理，我们使用强度差提取特征，并使用光流估计摄像机运动（CM）homography，将其与之前的CMs相乘以计算CP homography。

介绍

视频拼接是缝合在移动摄像机上捕捉到的多帧视频技术。
经典的工作方法是采用相机路径（CP），它是连续帧中的homograpgy的乘积，但是不依赖于homography的直接计算。这种方法性能还是可观的，主要有两项不足：
1）需要过多的处理时间，不适合用于实时系统的处理，传统电脑需要3-4秒的时间去缝合分辨率为1280x720的视频的两帧。 2）连续的复合误差将会导致不对齐的现象，因此在出现cp误差的情况下会出现空间伪影
主要为了解决上述两个大问题，本文提出了相机路径估计（CP）和单应性矩阵细化，

相关工作

图像拼接

核心问题是如何消除视差产生的错位，解决方式主要是两种：1）接缝 2）warping

视频拼接

核心问题是如何将错位进行消除以及尽可能的缩短处理时间

本文方法

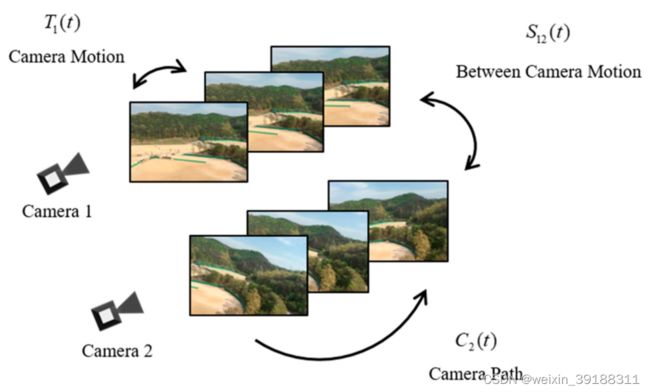
运动模型：空间运动模型和时间运动模型，单应性矩阵用于获取运动模型。空间运动模型是相机间的单应性矩阵，表示在同一帧中多个输入之间的单应性矩阵，$S_{nm}(t)$是帧t中相机n到相机m的相机间homography（BC）;时间运动模型是由连续的CMs和CPs组成，CMs是相同相机在相邻帧之间的单应性矩阵，$T_n(t)$是帧t-1到帧t之间的相机n的相机运动（CM）,即$T_n(t)=CM$;相机路径CP是由多个相机运动CM累积得到，即$CP=\prod C{M}_s={\prod }_{t=1}^t{T}_n(t)$其中，相机路径CPs对于精准视频拼接来说是重要的组件成分，CP可以写为$C_n(t)$：帧t中的相机n，表达式如下：

$$\begin{gathered} CP=C_n(t)=T_n(t)C_n(t-1) \\ =T_n(t)\cdots T_n(2)T_n(1)=C{M}_t\cdots C{M}_{2}C{M}_1 \end{gathered}$$

如下是各种运动模型的示意图：

如下探究CP和BC之间的联系，下面等式展示了对应的描述：

$S_{12}(t)=C_1(t)S_{12}(0)C_2^{-1}(t)$

其中，$C_1(t)$和$C_2(t)$是相机1和相机2的CP；$S_{12}(0)$是初始帧的BC homography，$S_{12}(t)$可以将摄像机1捕获到的图像坐标转换到摄像机2的坐标。
下图展示了几者之间的联系：

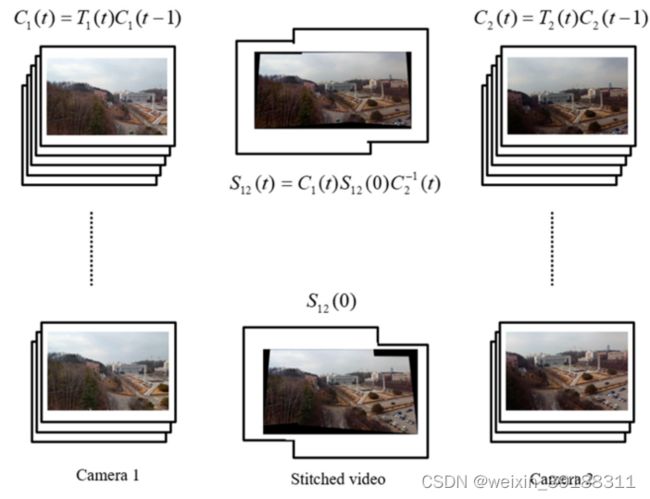
然而，BC $S_{12}(t)$不用于帧之间的坐标变换。由于参考帧发生了显著变化，因此变换帧的运动可能会变得更剧烈。因此，将参考帧设置为第一帧，以获得使用固定摄像机拍摄的稳定结果。对于这项工作，我们需要扭曲运动warping motions（$WMs$），将矩阵从第一帧的参考帧映射到当前帧。我们将$WM$表示为$W_n(t)$，其中的摄像机n位于帧t处。$WMs$是由初始BC homography和相机路径CP组成，下图是上述几种运动模型之间的关系，其中，每个输入由$WM$在摄像机1的第一帧的基础上进行变换。

表示WM的方程可以写成:

$W_1(t)=C_1^{-1}(t)$

$W_2(t)=S_{12}(0)C_2^{-1}(t)$

其中$W_1(t)$和$W_2(t)$分别是摄像机1和2的$W{M}_s$，$C_1(t)$和$C_2(t)$是CP，$S_{12}(0)$是摄像机1和2在第一帧处的初始BC。

算法框架

第一步

获取多个摄像机的输入，进行粗略的同步

第二步

估计相机路径CP，应用网格上的帧的强度提取特征，利用光流法跟踪特征生成匹配点

第三步

第三步是细化BCs。由于CP不准确，有时会在结果中观察到错位。为了消除错位，我们使用块匹配重复估计误差运动。然后，将误差运动的倒数乘以当前BC。

第四步

最后一步执行warping和混合。对于warping阶段，我们使用$CP$和$B{C}_s$估计$W{M}_s$，并通过将$W{M}_s$乘以帧来生成warping图像。在混合阶段，我们去除了由两幅图像之间的强度差异产生的视觉接缝。在我们的框架中，采用多波段混合作为混合方法。

CP 估计

提出的CP估计方法对该领域的贡献主要有两个原因：（1）均匀特征提取，（2）快速特征匹配。第一种方法是基于网格的均匀特征提取。CP估计受特征分布的敏感影响。例如，假设特征在某个区域上密集聚集；创建局部单应性，而不是全局单应性。该局部单应性产生的结果包括错位伪影。因此，特征应均匀分布。对于均匀分布，使用网格提取特征。该方法的第二个贡献是使用光流进行快速特征匹配。传统上，在匹配特征时，计算描述符需要很长的处理时间。因此，我们需要定义一种没有描述符的新特征匹配方法。在该方法中，通过使用光流跟踪特征来获得匹配点。下图显示了CP估计方法的流程图。

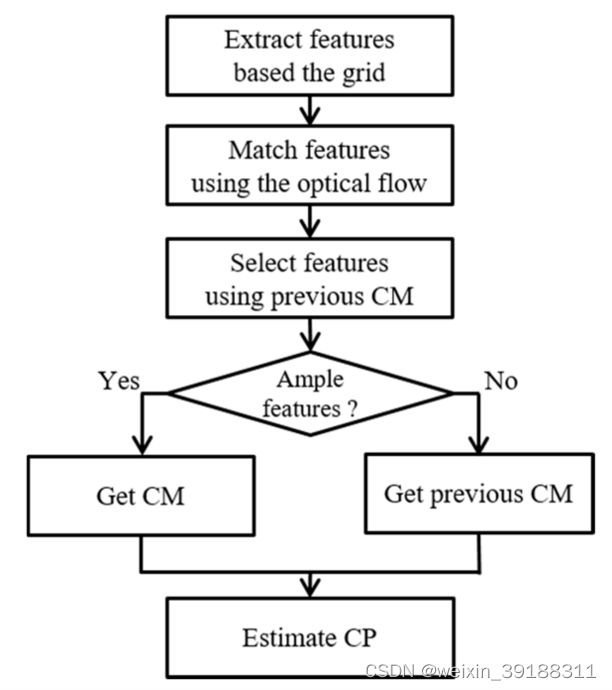
特征提取

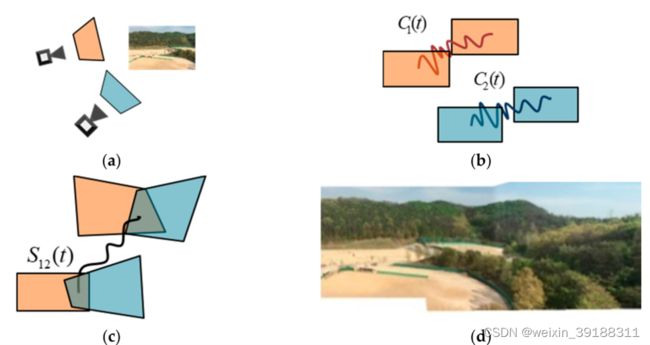
基于网格的特征提取过程由两个步骤组成：（1）在帧上面分割以实现特征的均匀分布；（2）使用相邻帧之间的差异强度进行特征提取。具体体现在：首先，我们将输入帧划分为网格。下图显示了划分为网格的输入。

其中绿线是网格线。根据经验，在高清分辨率（1280×720像素）下，网格大小设置为70。网格的顶点成为提取特征的潜在特征。将图像分割成网格后，我们在网格顶点上选择候选特征。其次，提取方法使用当前帧和前一帧之间的强度差：

$\left|I_t(x,y)-I_{t-1}(x,y)\right|>{\tau }_i$

其中x和y是网格顶点上的坐标，$I_t(x,y)$和$I_{t-1}(x,y)$是当前时间t和前一时间t的强度;而$ta{u}_i$是阈值（我们使用$ta{u}_i$=5）。下图（a）显示了特征提取。
基于网格的特征提取不仅快速，而且稳定。我们的提取方法比其他方法产生更稳定的CM。例如，当将一般方法应用到帧中时，例如使用哈里斯角点检测，我们经常确认特征密集分布在某些区域，上面图（b）所示，因为该方法在高纹理区域（例如建筑物、树木）上产生的特征比纹理较差的区域（例如天空、道路）更多。有偏特征分布基于特征数最多的平面估计局部单应性。使用局部单应性估计CM，我们得到的结果很差，集中在具有许多特征的平面上。相反，我们提出的方法提取均匀特征。该方法估计全局单应性，其产生的结果优于任何单个局部单应性。

特征匹配

在传统的拼接方法中，匹配方法使用包括高维描述子（descriptor）在内的特征。为了生成描述子，匹配算法执行了一个复杂的过程。这种方法需要更多的时间才能获得结果。因此，我们需要新的特征匹配方法，而不使用描述子。对于没有描述子的快速匹配方法，我们使用光流方法。光流法是一种跟踪算法，旨在找到相邻帧之间的目标。光流法的目的是跟踪物体。然而，我们使用光流来跟踪特征，而不是对象。我们使用特征的位置作为光流的种子，并跟踪特征。由于当前帧和前一帧之间区域的模式相似，可能会观察到跟踪误差。为了消除跟踪误差，我们使用以下等式：
$d_1\left(p,p_{\text{track }}\right)/N(w)<{\tau }_e$

其中$d_1(p，p_{track})$是初始点$p$和跟踪点$p_{track}$之间的$L1$距离，$N(w)$是搜索窗口中的像素数，${\tau }_e$是确定点是否正确的阈值（我们使用${\tau }_e$=5）。通过使用此约束，消除了跟踪误差。

特征选择

通常，帧的特征分布是相似的，因为帧之间的时间差非常小。然而，由于照明的变化或摄像机的剧烈运动，往往会出现不同的特征分布。这一事实往往导致结果不稳定。为了防止这些情况，我们在估计CM之前实施了特征选择过程。特征选择可以防止两种不需要的情况：（1）与前一帧比较不同的特征分布，（2）没有识别特征点。首先，特征的分布有时不同于前一帧的分布。这种情况会产生不连续的结果。为了解决这个问题，假设当前和以前的$C{M}_s$之间几乎没有差异。利用这个假设，我们使用前一个$CM$变换当前特征。然后，我们计算由先前$CM$转换的特征与使用光流方法跟踪的特征之间的欧几里德距离。该距离将与阈值做比较，得到inliners，最后，使用RANSAC由inliners估计$C{M}_s$，并与之前的CP相乘以估计新的CP,

$d_2\left(p_{\text{pre }},p_{\text{track }}\right)<{\tau }_S$

其中$d_2(ppre，ptrack)$是由先前CM转换的特征ppre和使用光流的跟踪特征ptrack之间的$L_2$距离。${\tau }_s$是阈值。我们将该阈值设置为${\tau }_s$=30。然后，使用RANSAC由估计CMs，并与先前CP相乘以估计新CP。其次，我们防止了在选择特征后提取少量inliners的情况。如果使用少量特征估计CM，则可能估计错误的CM。为了防止这种不良情况，我们采用了一种简单的方法，用以前的配置管理替换当前的配置管理。由于相邻$C{M}_s$之间几乎没有差异，因此可以利用此方法。

单应性矩阵精化

我们将介绍如何完善BCs。在视频拼接过程中，使用下面的等式在公共空间上表示不同摄像机的坐标。

$S_{12}(t)=C_1(t)S_{12}(0)C_2^{-1}(t)$

$W_1(t)=C_1^{-1}(t)$

$W_2(t)=S_{12}(0)C_2^{-1}(t)$

然而，BC可能包括由不准确的$C{P}_s$引起的误差，这些误差是由于剧烈的摄像机移动或强度变化而错误估计的。因此，我们建议使用块匹配来实现BC细化。
$\mathrm{BC}{\bar{S}}_{12}(t)$定义如下:
${\bar{S}}_{12}(t)={\bar{C}}_1(t)S_{12}(0){\bar{C}}_2^{-1}(t)$,

${\bar{S}}_{12}(t)=E_{12}(t)C_1(t)S_{12}(0)C_2^{-1}(t)$,

其中${\bar{C}}_1(t)$和${\bar{C}}_2(t)$是包括误差运动$E_{12}(t)$的CP的观测值，BC观测值和理想BC之间的关系方程估计为：

${\bar{S}}_{12}(t)=E_{1,2}(t)S_{12}(t)$

实际上，相邻帧之间的误差运动对错位影响很小。然而，误差是随着时间积累的。在最后一帧，结果包括明显错位的伪影。因此，BC的观察必须通过与$E_{12}(t)$的逆相乘来更新，如下所示：

${\hat{S}}_{12}(t)=E_{12}^{-1}(t){\bar{S}}_{12}(t)$

其中${\hat{S}}_{12}(t)$是精炼BC。实际上，使用${\hat{S}}_{12}(t)=E_{12}^{-1}(t){\bar{S}}_{12}(t)$来扭曲图像，估计精细$W{M}_s{\hat{W}}_1(t)$和${\hat{W}}_2(t)$:

${\hat{W}}_1(t)={\bar{C}}_1^{-1}(t)$

${\hat{W}}_2(t)={\hat{S}}_{12}(t){\bar{C}}_2^{-1}(t)=E_{12}^{-1}(t){\bar{S}}_{12}(t){\bar{C}}_2^{-1}(t)$

为了更新细化BCs，应使用特征和细化特征估计误差运动$E_{12}(t)$，这是理想的缝合特征，如下图所示。

换句话说，找到了细化特征的位置。寻找精细特征的最简单方法是使用SIFT和FLANN的方法。然而，由于处理时间长，这种方法不适用于实时系统。因此，我们使用块匹配来估计误差运动。块匹配是一种查找模板位置的匹配算法。为了找到精确的特征，围绕右帧的特征和搜索ROI构建模板，这是块匹配的搜索范围，并构建在左帧上，如上图（b）所示。然后，通过实现块匹配算法来估计误差运动。

下图所示了单应性细化的流程图。

在第一步中，我们在第一帧使用SIFT和FLANN计算初始BC。虽然该初始步骤具有较长的处理时间，但准确估计初始业务连续性很重要，该初始业务连续性可作为精细业务连续性的参考。在第二步中，我们重用在CP估计中获得的来自右帧的特征来构造模板和搜索ROI。在第三步中，我们分别在扭曲的右帧和左帧中的扭曲特征周围形成大小（n×n）的模板和大小（m×m）的搜索ROI。我们分别将n、m定义为9、21。在第四步中，我们执行块匹配以估计误差运动。块匹配使用归一化互相关（NCC）来测量模板和搜索ROI之间的匹配率：

$r(x,y)=\frac{{\sum }_{x^{\prime },y^{\prime }}\left(i_t\left(x^{\prime },y^{\prime }\right)i\left(x+x^{\prime },y+y^{\prime }\right)\right)}{\sqrt{{\sum }_{x^{\prime },y^{\prime }}{i}_t{\left(x^{\prime },y^{\prime }\right)}^2{\sum }_{x^{\prime },y^{\prime }}i{\left(x+x^{\prime },y+y^{\prime }\right)}^2}}$

其中$x$和$y$是扭曲帧中的像素坐标，x0和y0是模板中的像素坐标，r（x，y）是NCC的值，i（x，y）和it（x，y）分别是扭曲帧和模板中的强度。我们选择r（x，y）最大的特征作为细化特征。最后，通过误差运动更新当前BCs，误差运动由使用RANSAC算法和（11）的精细匹配点估计。
该初始业务连续性可作为精细业务连续性的参考。在第二步中，我们重用在CP估计中获得的来自右帧的特征来构造模板和搜索ROI。在第三步中，我们分别在扭曲的右帧和左帧中的扭曲特征周围形成大小（n×n）的模板和大小（m×m）的搜索ROI。我们分别将n、m定义为9、21。在第四步中，我们执行块匹配以估计误差运动。块匹配使用归一化互相关（NCC）来测量模板和搜索ROI之间的匹配率：

$r(x,y)=\frac{{\sum }_{x^{\prime },y^{\prime }}\left(i_t\left(x^{\prime },y^{\prime }\right)i\left(x+x^{\prime },y+y^{\prime }\right)\right)}{\sqrt{{\sum }_{x^{\prime },y^{\prime }}{i}_t{\left(x^{\prime },y^{\prime }\right)}^2{\sum }_{x^{\prime },y^{\prime }}i{\left(x+x^{\prime },y+y^{\prime }\right)}^2}}$

其中$x$和$y$是扭曲帧中的像素坐标，x0和y0是模板中的像素坐标，r（x，y）是NCC的值，i（x，y）和it（x，y）分别是扭曲帧和模板中的强度。我们选择r（x，y）最大的特征作为细化特征。最后，通过误差运动更新当前BCs，误差运动由使用RANSAC算法和（11）的精细匹配点估计。

#注：以上内容均为本人阅读大神论文摘选各自内容产生的笔记，没有进行任何出版或者其他行为，本博客仅供有需要的人学习成长浏览！！！