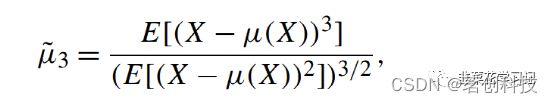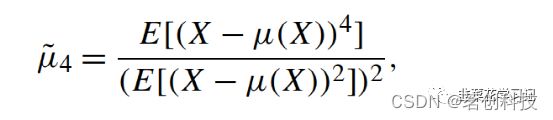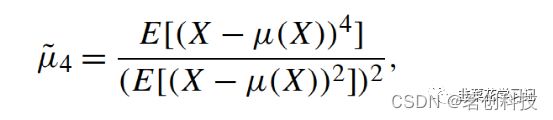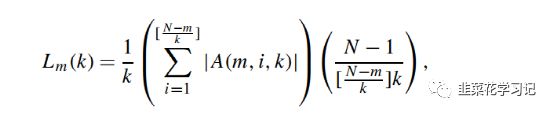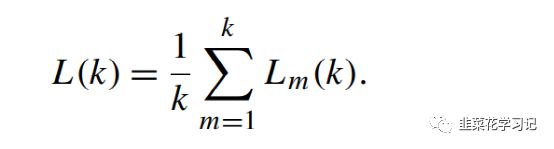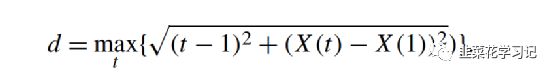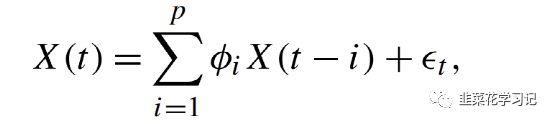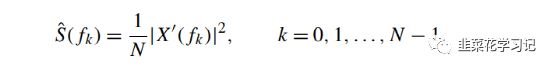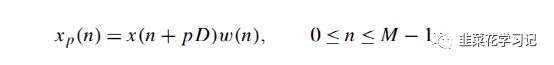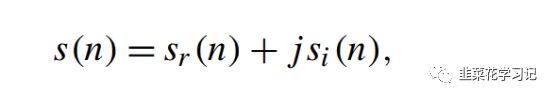时域、频域、时频特征提取技术

文章来源于微信公众号（茗创科技），欢迎有兴趣的朋友搜索关注。

一、时域特征提取技术

当我们想要研究一个生物信号时，有时从原始信号中获取的信息并不明显。因此，需要提取一些特征来表示信号。可以研究代表信号波形的特征，也可以把信号的样本看作是来自随机源，因此可以得到一个分布，从中提取信息。通过分析它们在这个分布中的统计特性，或者在某些情况下的混沌行为，可以从混沌分形理论中进行测量。下面列出了一些提取原始生物电信号(时域)特征的最流行的方法。

1、从波形中提取特征：提取的最直接的特征是可以直接从信号中观察到的。虽然很简单，但对生物电信号十分有用。

①零交率（Zero crossing rate，ZCR）

零交率或称过零率(ZCR)测量的是波形过零轴的次数。对于一个信号X(t)，计算同时满足以下两个条件的次数就可以得到该信号：

其中ϵ为一个阈值，以避免由于噪声而误算过零次数。

②坡度符号变化

另一种分析波形的方法是计算斜率信号变化的次数。对于信号X(t)，可以通过计算满足以下两个条件的次数来获得：

其中ϵ为一个阈值，以避免由于噪声导致坡度变化的计算错误。

③波长

最后，另一种分析信号的方法是测量其波长(WL)。可以通过以下计算获得：

 

其中，n表示信号中的样本数量。

2、统计值：通过分析信号的均值(μ)、最大值、最小值、和的统计特征来提取信号中的信息。此外，还可以通过相对不常用的统计方法来进行分析。

①偏度

偏态(μ3)是测量一个分布在均值附近的不对称程度。对于信号X(t)，偏度定义如下：

 

其中E[·]为期望值。

 

②峰度

峰度(μ4)是指分布曲线在均值附近的形状。对于信号X(t)，峰度定义如下：

 

其中E[·]为期望值。

3、混沌分形理论的特征：需要注意的是，有些生物电信号是混乱的，所以需要利用分形特征来表示信号。下面描述了几种分析混沌信号的方法。

①香农熵

香农熵S(x)是随机数据源产生信息的平均速率。香农熵越大，过程中新值给出的信息就越大。对于信号X(t)，熵的定义如下：

其中p(xi)是得到xi值的概率。

②Higuchi分形维数

Higuchi分形维数(HFD)估计信号在时域的分形维数。对于信号X(t)，HFD的计算如下：首先，从原来的时间序列X(t)，计算一组新的时间序列，如下所示：

对于m=1，2，…，k和k=1，kmax·kmax通常定义在6到16之间。根据得到的新序列，计算的曲线Lm(k)的长度，计算公式如下：

其中A(m，i，k)=X(m+ik)-X(m+(i-1)k)，N为原始时间序列的长度。Lm(k)对每个k取m的平均值，得到

最后，根据ln(L(k))比ln(1/k)的曲线，将HFD估计为最小二乘法的斜率：

③Katz分形维数

Katz分形维数(KFD)通过分析时间序列的波形来估计分形维数。对于信号X(t)， KFD定义为：

其中m是信号中的样本数，L是信号的总长度，即，

以及d为波形的平面距离，定义为信号中第一个点到最远点的距离：

④广义Hurst指数(GHE)

广义Hurst指数(GHE)，记作H(q)，用于时间序列分析和分形分析，通过分析增量分布的q阶矩来测量尺度特性。对于时间序列X(t)，可由以下关系式得到广义Hurst指数H(q)：

由X(t)给出，t=ν，2ν，…，kν，T。(观测周期T和时间分辨率ν) 对于q=1，广义Hurst指数与原始Hurst指数密切相关，原始Hurst指数测量时间序列的混沌程度或不可预测性。

4、自回归模型：自回归模型是分析信号的另一种方法；它包括信号X(t)在给定时间t=τ内取过去的值进行建模。用A(p)表示，其中p描述模型的阶数。也就是说，需要前多少次的观测来预测信号的当前值。对于信号X(t)，一个p阶自回归模型如下，

其中ϵt是噪声参数。

二、频域特征提取技术

基于频域分析的特征提取技术旨在利用信号的频谱信息，如不同频率上的振幅或相位。其原理是生物电信号的频谱信息可能会根据不同的实验条件或情况发生变化，因此它可以编码与任务相关的信息，揭示生物电信号是如何产生的。原则上，任何生物电信号都可以近似为以不同频率振荡的复指数或正弦波的叠加。因此，频域分析可以用来计算信号的频谱信息，从而作为提取可靠特征的重要技术。

频域特征的几个优点：(1)识别信号变化或模式的可行性更高，而不仅仅只是观察时域信息；(2)可能比时域特征提供更强的鉴别能力，而时域特征却取决于信号的性质；(3)由于只使用某些频率的频谱信息，因此可以获得低维表征；(4)由于具有快速且高效的频谱信息计算算法，因而计算成本较低；(5)不仅可以利用单个频率的频谱信息，而且可以利用频带的频谱信息，这在某些应用中可能更方便；(6)利用信号和应用程序的性质信息，可以预先选择用于计算频谱信息来获得特征的频率。

图1显示了如何使用频域分析作为特征提取技术。在此例中，在两种不同的条件或情况下记录EEG信号，代表两种不同的类别，即无运动和运动。在时域特征上没有显示任何差异或明显特征。两种信号的振幅和振荡活动相似，无法识别出差异。然而，从频域上得到的频谱信息表现出类依赖差异。注意，这一特征是直接从频域分析获得的频谱信息中提取的。

图1

下面介绍了三种常用且广泛用于计算生物电信号频域特征的方法，即离散傅里叶变换(DFT)、非参数功率谱密度(PSD)和基于参数自回归模型的频谱(ARS)。

1、离散傅里叶变换(DFT)

傅里叶变换(FT)是一种基本的数学工具，允许将信号表示为无限复指数(或正弦信号)的和。因此，它表示合成信号所需的复指数(或正弦波)的相对振幅和相位。“确定性的”有限持续时间离散信号x(n)=[x(0)，x(1)，…，x(n-1)]T的FT定义为：

其中频率变量为f。注意，X(f)是复的，连续的，且周期等于1。出于实际考虑，有必要计算X(f)的离散型版本。为了实现这一点，简单地在一个基本周期内对X(f)取N个等距的样本，也就是说，在N个等间隔的频率上对X(f)进行采样fk=k/N，k=0，1，…N-1，其中0≤fk＜1。这就产生了离散傅里叶变换(DFT)，它是计算FT样本集的标准方法：

注意，DFT提供了长度为N的信号x(n)的FT的N个样本{X(fk)}，其中每个样本对应一个频率f0，…，fN-1。在许多情况下，需要增加计算DFT的频率数目。为此，只需在信号x(n)上添加0来增加其总长度。这个零填充过程不提供任何额外的信息或改变结果的DFT，然而，它增加了计算DFT的等间隔频率的密度。值得注意的是，实际上DFT可以通过快速傅里叶变换(FFT)算法高效且容易地计算出来。FFT可用于计算有限持续时间离散信号的FT。

当有限持续时间的离散信号x(n)是以每秒fs采样率进行采样时，DFT的相关频率为fk=fs· k/N，k=0，2，…，N-1。然而，半周期的DFT就足以获得真实信号的完整频谱信息。然后，可以从DFT中提取的特征是频率范围从0到fs/2的幅度、相位或两者。

2、功率谱密度(PSD)

通常，FT和DFT被定义为确定性信号，然而，在许多情况下，生物电信号可以更好地描述和建模为随机过程。对于这类信号，基于频域分析的特征提取技术需要估计频谱特征，特别是功率谱密度(PSD)，它从根本上显示了信号功率作为频率的函数是如何分布的。

估计PSD的一种方法是非参数频谱分析，在这种方法中，对数据及其生成方式不做任何假设或建模。唯一的条件是限制为二阶平稳且遍历的随机信号。如果满足这个条件，随机信号S(f)的真正PSD等于自协方差序列的FT，这需要无穷多个样本和实现。然而，在实际应用中，只有一个有限长度的随机信号。在这种情况下，PSD的可靠估计量

(f)近似无偏性，即E{

(f)}≈S(f)和低方差，即Var{

(

f k)}≈0。

给定有限长平稳随机信号x(n)=[x(0)，x(1)，…，x(N-1)]T，计算PSD作为信号自相关序列的DFT。这就引出了估计PSD的周期图方法：

其中，X′(fk)是加窗信号x′(n) =x(n)ω(n)的DFT，ω(n)是一个长度为N的窗函数。当ω(n)是一个矩形窗口(即对于所有n，ω(n)=1)时，得到的PSD估计方法称为周期图。相反，当ω(n)为非矩形窗口时(如Hanning或Hamming)，得到的PSD估计方法称为修正的周期图。非矩形窗口ω(n)的作用是减轻由于信号长度有限而引起的估计误差，如泄露(一个频率的功率泄露到其他频率，从而产生误导的频率成分)。周期图估计和修正的周期图估计的局限性是它们是不一致的(即N→Var{

(f k)}不会趋于零)，这意味着估计的PSD具有很高的变异性，不会随着信号长度的增加而减小。

为了减少高方差的固有缺点，可以从平稳随机信号x(n)的不同实现中计算出的K个周期图。均值的含义很简单，K独立同分布随机变量和的方差等于1/K乘以每个随机变量的方差。然而，实际上，我们只有一个信号x(n)(长度为N)，但可以将其细分为P个更小的段(长度为M＜N)，然后对所有分段的周期图求平均。这就产生了Welch-Barlett周期图法，或简单的平均周期图法，该方法广泛应用于众多领域，包括EEG信号的频率分析。给定有限长平稳随机信号x(n)=[x(0)，x(1)，…，x(N-1)]T，将其细分为以下小段：

其中xp(n)，p=0，1，…，P-1是P个长度为M的段，ω(n)是长度为M的窗函数，D是段之间的位移。在D=M的情况下，位移等于段长，因此所有段都是共轭的，当D＜M时，位移小于段长，因此段重叠，且重叠大小为M-D。然后，使用公式

计算第p段的周期图p(fk)。由此可见，PSD估计是P周期图的平均值：

同样，在0到fs/2范围内的单侧PSD足以捕获整个信号频谱信息，前提是信号x(n)是真实的，并以每秒fs采样，这适用于真实的生物电信号应用研究。因此，从估计的单侧PSD

(fk)中提取的特征，无论是用周期图、修正的周期图或平均周期图计算得到的，都是单个频率的功率或预定义频带内的平均功率，可以根据应用情况预先选择。

3、基于自回归模型的频谱估计

另一种估计PSD的方法是基于参数的方法。在这种情况下，对于数据及其如何生成的具有一些假设。具体来说，自回归建模假设观测到的信号x(n)是一个全极点滤波器的输出，在该滤波器中输入高斯白噪声(WGN)。因此，滤波器的系数是模型参数，必须从数据中进行估计。给定信号x(n)，上述时域特征提取技术中介绍的自回归(AR)模型，记为A(P)，这里改写为：

其中ai为滤波模型的第i个系数，P为模型阶数，ε~N(0，

)为预测误差。由傅里叶变换分析可知，滤波器输出信号的频谱功率x(n)可以简单地计算为：

注意，唯一要估计的参数是模型系数，而模型顺序必须预先定义。基于AR模型的频谱分析的优点是能够表征生物电信号中常见的峰值频谱成分，如EEG和ECOG。然而，在任何参数化方法中，其有效性取决于模型的正确选择。因此，合适的模型阶数选择是正确获取和描述信号的真实频率成分和提取适当特征的一项重要任务。

一旦定义了模型的阶数，就有几种方法来估计AR模型系数a1，…，ap和噪声方差

。例如，Burg方法常用于EEG信号分析和基于EEG的脑机接口应用。与基于傅立叶的方法一样，使用AR模型从估计的PSD计算出的特征集是给定频率或频带下的功率值。

三、时频特征提取技术

通常情况下，时域和频域特征提取方法的一个局限性是，由于信息只从一个域进行计算，因此丢弃了具有高分辨力的重要特征。例如，时域特性不提供振荡信息，而在频率分析的情况下，并没有提供详细的频谱信号随时间变化的信息，但这些是ECG和EEG等研究的重要关注点。对于这一限制，可通过时频分析来解决，如短时傅里叶变换(STFT)，Morlet小波(MW)，基于滤波器的希尔伯特变换(FHT)。

时频方法是一种信号处理工具，可以描述信号在一段时间内的频率内容。给定一个离散时间信号x(n)，时频方法可以提供一个二维表示x(n，f)，它是时间和频率的复函数。因此，可以提供信号的不同频率成分的幅度和相位如何随时间变化。请注意，信号的时频表示，无论是幅度还是相位，都可以是一组特征，通过卷积神经网络等新型的基于深度学习的分类器直接呈现2D图像。

1、短时傅里叶变换(STFT)

为了计算STFT，将离散时间信号x(n)细分为P个连续的长度为M的小段，并对每个段计算DFT：

其中xp(n)=x(n+pD)是长度为M的第p段；ω(n)是一个长度为M的数据窗函数，其边缘逐渐变细，以避免引入频谱伪影；p=1，2，…，P表示每个连续的段，因此表示时间；k=0，1，…，M-1表示计算DFT的点，因此表示频率，D表示段之间的位移。计算DFT的点为k=0，1，…，M-1表示频率fk=k/M，k=0，2，…，M-1或0≤fk＜1，虽然零填充可以用来增加频率的密度。注意，在连续的段之间存在重叠(当D＜M)时，它补偿了加窗函数在窗边的信号衰减。图2说明了如何计算短时傅立叶变换。

图2

STFT的幅度(|X(p，k)|)被称为谱图。值得注意的是，短窗可以获得时域的高分辨率，但同时也导致了频域的低分辨率。反之亦然。这揭示了在时间和频率分辨率之间存在一种内在的平衡，这种平衡需要根据生物电信号的特征来定义。

2、Morlet小波(MW)

基于MW的时频分析是将观测信号与一种具有一定特征的特殊函数进行卷积运算。函数可以有多种基本形式，但在Morlet小波情况下，是基于复正弦-高斯函数的，其定义如下：

其中fi是对一段时间内的信号进行分析的频率，A=(σtπ-1/2)-1/2是归一化常数，总能量是1，σt=1/(2πσf)是时域宽度，Q=fi/σf是一个用来定义Morlet小波周期数的恒定比率(高Q增加频率分辨率，低Q增加时间分辨率)。对于EEG信号的时频分析，一般将Q定义为7。

3、基于滤波器的希尔伯特变换(FHT)

这种时频方法的核心是希尔伯特变换，它允许对信号的每个频率成分引入π/2的相移。因此，给定一个离散实值信号sr(n)，可以通过希尔伯特变换来定义下面的复信号：

其中，si为sr(n)的希尔伯特变换，s(n)定义为解析信号，它是复数，因此体现了每个时间瞬间最强频率成分的幅值和相位。然而，对于宽频带信号，不可能确定幅值和相位与什么频率相关联。当需要获得在某一特定频率下的每个时刻的幅值和相位时，实际信号必须是窄带的。

用这些思想计算任意带宽信号x(n)的时频表示如下：用一组窄带带通滤波器得到窄带信号xfi(n)，其中fi=f1，f2，…，fM表示滤波器的中心频率。对每个窄带信号xfi(n)进行希尔伯特变换，得到复解析信号。则可以构造时频表征X(n，fi)，其中n=0，1，…，N-1，fi=f1，f2，…，fM。正是利用带通滤波器，然后计算希尔伯特变换，才产生了基于滤波器的希尔伯特变换(FHT)时频方法。由于X(n，fi)是复数，因此可以直接计算每个频率在每个时间的幅度和相位。

参考来源：

https://doi.org/10.1016/B978-0-12-820125-1.00014-2

文章来源于微信公众号（茗创科技），欢迎有兴趣的朋友搜索关注。