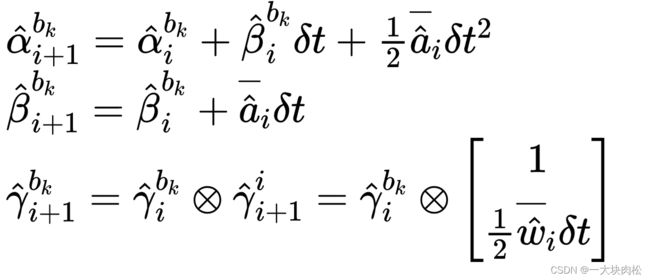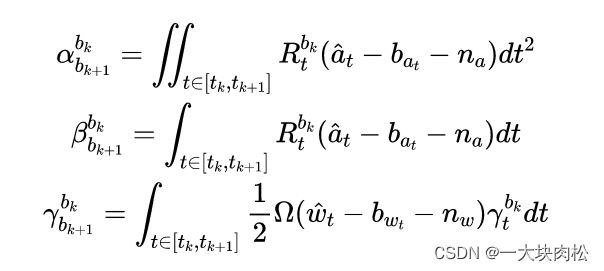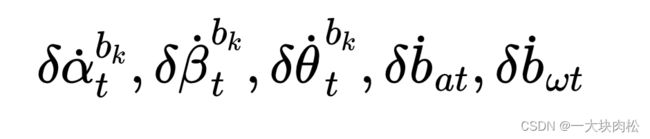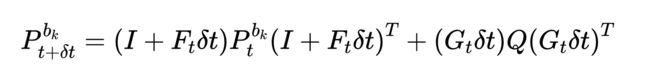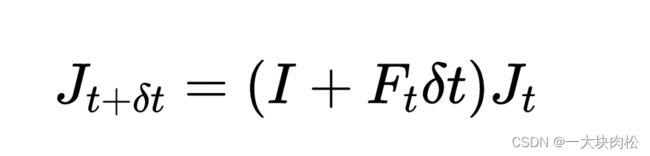IMU预积分--详细推导过程
一、提前了解
二、预积分的目的
1.IMU通过加速度计和陀螺仪测出的是加速度和角速度，通过积分获得两帧之间的旋转和位移的变换；
2.在后端非线性优化的时候，需要优化位姿，每次调整位姿都需要在它们之间重新传递IMU测量值，需要重新积分，这将非常耗时，为了避免重新传递测量值，所以采取预积分策略。
三、进入预积分主题
1.IMU模型
其中：
2.当前时刻的PVQ的连续表达形式
对图像第 k k k 帧和第 k + 1 k+1 k+1 帧之间的所有IMU进行积分，对应的IMU坐标系为 b k b_k bk 和 b k + 1 b_{k+1} bk+1 ，根据k时刻的数据，积分求得 k + 1 k+1 k+1 时刻的数据，求出的是在世界坐标系下的值：
其中：
Δ t k Δt_k Δtk ：表示[k,k+1]之间的时间间隔
q t b k q^{bk}_t qtbk：表示在本体（IMU）坐标系下，t 时刻到 b k b_k bk时刻位姿的变换矩阵 。
推导过程中旋转采用四元数表示。
对于上式中，第三个公式的推导过程如下：
首先需要先了解四元数的基本知识：
（1）四元数由实部和虚部构成，可以将实部写在前面，也可以将虚部写在前面，本文将实部写在前面：
q = [ q 0 , q 1 , q 2 , q 3 ] = [ s , v ⃗ ] q=[q_0,q_1,q_2,q_3]=[s,\vec{v}] q=[q0,q1,q2,q3]=[s,v]
即： q = q 0 + q 1 i + q 2 j + q 3 k q=q_0+q_1i+q_2j+q_3k q=q0+q1i+q2j+q3k （虚部写在前）
（2）四元数与旋转向量 ( n ⃗ , θ ) (\vec{n},\theta) (n,θ)的转换：
q = [ c o s θ 2 n ⃗ s i n θ 2 ] q=\begin{bmatrix} cos\frac{\theta}{2}\\ \vec{n}sin\frac{\theta}{2} \\ \end{bmatrix} q=[cos2θnsin2θ]
当发生一个微小的旋转，即旋转角度趋近于0，则有：
（3）四元数求导：
w w w：表示的是角速度，上式中对角度进行求导，得到角速度
由以上四元数的基本知识可以得到：第三个公式的推导过程如下：：
针对上述2.当前时刻的PVQ连续表达形式可知，若要求得当前时刻的旋转、位置、速度，需要前一时刻的状态量，但是当这些状态改变时，我们就需要重新传递IMU的测量值，特别是在基于优化的算法中，每次调整位姿都需要在它们之间重新传递IMU测量值，这种测量策略非常耗时，为了避免重新传递测量值，采用预积分算法。
通俗的解释：根据上一时刻计算出当前时刻的PVQ，当后端对上一时刻的值进行优化时，则需要根据优化好的值，重新计算当前帧的PVQ。
3.当前时刻的PVQ的中值法离散表达形式
对第 i i i个IMU时刻到 i + 1 i+1 i+1时刻的IMU进行积分
其中：
i i i 表示的是在 [ t k , t k + 1 ] [t_k,t_{k+1}] [tk,tk+1] 中IMU测量值对应的离散时刻；
δ t \delta{t} δt 是IMU测量值 i i i 和 i + 1 i+1 i+1 之间的时间间隔。
由以上四元数的基本知识可以得到：第三个公式的推导过程如下：：
其中
即取中值作为 i i i 时刻的预测值
q i q_i qi：用四元数表示，上式中表示imu坐标系到世界坐标系的变化。
4.两帧之间PVQ增量的连续形式
文章开始讲述，预积分的目的，在后端进行非线性优化的时候，需要迭代更新 k k k帧的 v v v和 R R R，这将导致我们需要根据每次迭代后的新值进行积分，这非常耗时，此时就需要将优化变量从第 k k k帧到第 k + 1 k+1 k+1帧的IMU预积分中分离出来，将2中各式左右两侧各乘 R w b k R^{b_k}_w Rwbk 得：
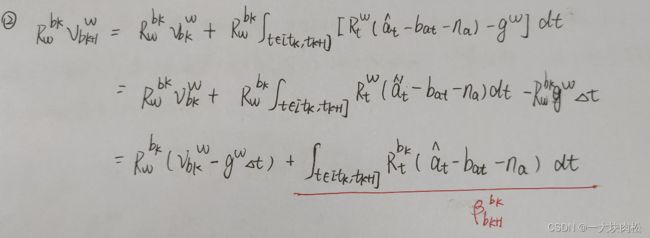
由以上三幅图可知：
积分结果
α b k + 1 b k \alpha^{b_k}_{b_{k+1}} αbk+1bk、 β b k + 1 b k \beta^{b_k}_{b_{k+1}} βbk+1bk、 γ b k + 1 b k \gamma^{b_k}_{b_{k+1}} γbk+1bk，可以理解为 b k + 1 b_{k+1} bk+1相对于 b k b_k bk的相对运动量；
其中：积分中与IMU的测量值以及偏置有关；
关于状态量中预积分公式中只与IMU的偏置有关，与其他的状态量无关。所以，当偏置估计发生变化时，若偏置的变化很小，则将 α \alpha α、 β \beta β、 γ \gamma γ按其对偏置的一阶近似来调整，否则就进行重新传递，这种策略为基于优化算法节省大量的计算，因为不需要重复传递IMU测量值。
则线性关系表达式为：
5.两帧之间PVQ增量的中值法离散形式
上式是直接根据预积分公式得出：
其中：
i i i：表示的是 [ t k , t k + 1 ] [t_k,t_{k+1}] [tk,tk+1] 中的IMU测量值对应的离散时刻；
δ t \delta t δt 是IMU测量值 i i i 和 i + 1 i+1 i+1 之间的时间间隔
其中：
6. 连续形式下PVQ增量的误差、协方差及Jacobian
接下来讨论
的增量的误差。
因为积分出来的值存在误差，所以需要对其进行分析处理。
（1）先知
IMU受到加速度计的偏置 b a b_a ba，陀螺仪偏置 b w b_w bw ，附加噪声 n a n_a na、 n w n_w nw 的影响。
假设附加噪声 n a n_a na、 n w n_w nw 符合高斯噪声
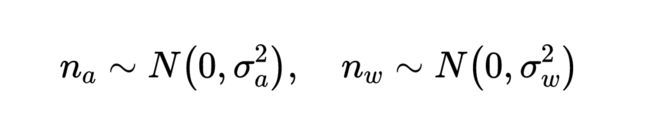
加速度偏置和陀螺仪偏置被建模为随机游走，其导数为高斯性的：
（2）误差项
对上述误差项分别进行求导：
接下来是详细的求导过程
（3）协方差
以上计算过程求出积分项误差的导数，根据导数的定义可得：
可得
\qquad δ t \delta t δt 的时间间隔，可以看出下一时刻（ t + δ t t+\delta t t+δt）的IMU的测量误差与上一时刻（ δ t \delta t δt）成线性关系。
\qquad 按此方式，可以根据当前时刻的值，预测出下一时刻的均值和协方差，上式给出了均值预测，同样可以得到协方差预测公式：
其中 P t b k P^{b_k}_t Ptbk表示t时刻的协方差， Q Q Q表示噪声项符合的协方差：
（4）Jacobian
7.离散形式下的PVQ增量的误差、协方差及Jacobian
（1）误差项
上述矩阵可以表示为：
δ Z k + 1 = F δ Z k + V n \qquad\qquad\delta Z_{k+1}=F\delta Z_k+Vn δZk+1=FδZk+Vn
（2）协方差
同理得到协方差公式：
P k + 1 = F P k F T + V Q V T \qquad \qquad P_{k+1}=FP_kF^T+VQV^T Pk+1=FPkFT+VQVT
其中 Q Q Q表示噪声项符合的协方差：
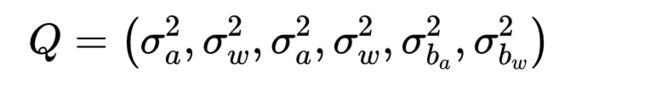
（3）Jacobian
J k + 1 = F J k \qquad \qquad \qquad J_{k+1}=FJ_k Jk+1=FJk
（4）补充对误差项求导的详细步骤
总结：终于结束了IMU预积分的推导过程，作为一个记录（tips看了好多大佬的博客）
参考博客：
VINS-Mono理论学习——IMU预积分 Pre-integration （Jacobian 协方差）
【VINS论文翻译】VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator
四元数对时间求导数