Scipy信号分析处理（基线漂移、滤波）（笔记01）

信号处理的知识：

• scipy.signal.detrend(): 从信号中删除线性趋势：

from scipy import signal
import matplotlib.pyplot as pl

t = np.linspace(0, 5, 100)
x = t + np.random.normal(size=100)
pl.plot(t, x, linewidth=3)
pl.plot(t, signal.detrend(x), linewidth=3)

效果展示：

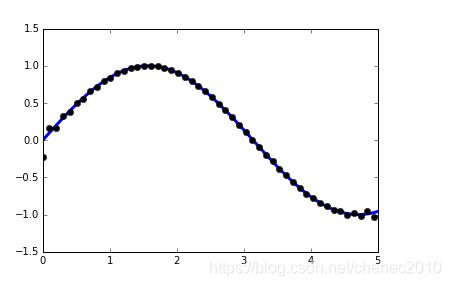
• scipy.signal.resample(): 用FFT从信号中抽出n个点。

t = np.linspace(0, 5, 100)
x = np.sin(t)
pl.plot(t, x, linewidth=3)
pl.plot(t[::2], signal.resample(x, 50), 'ko')

效果展示：

---

信号的滤波介绍：

scipy模块使用Python实现简单滤波处理，包括内容有1.低通滤波，2.高通滤波，3.带通滤波，4.带阻滤波器。

简单的理解就是低通滤波指的是去除高于某一阈值频率的信号；高通滤波去除低于某一频率的信号；带通滤波指的是类似低通高通的结合保留中间频率信号；带阻滤波也是低通高通的结合只是过滤掉的是中间部分。

通过时域转换为频域，在频域信号中去除相应频域信号，最后在逆转换还原为时域型号。

可以消除一些干扰信号，以低通滤波为例，例如我们如果只是统计脉搏信号波形，应该在1Hz左右，却发现波形信号上有很多噪音，这些噪音都是成百上千Hz的，这些对于脉搏信号波形就属于无用的噪音，我们就可以通过低通滤波器将超出某一阈值的信号过滤掉，此时得到的波形就会比较平滑了

1).低通滤波

这里假设采样频率为1000hz,信号本身最大的频率为500hz，要滤除400hz以上频率成分，即截至频率为400hz,则wn=2*400/1000=0.8。Wn=0.8

from scipy import signal

b, a = signal.butter(8, 0.8, 'lowpass')   #配置滤波器 8 表示滤波器的阶数
filtedData = signal.filtfilt(b, a, data)  #data为要过滤的信号

2).高通滤波

这里假设采样频率为1000hz,信号本身最大的频率为500hz，要滤除100hz以下频率成分，即截至频率为100hz,则wn=2*100/1000=0.2。Wn=0.2

from scipy import signal

b, a = signal.butter(8, 0.2, 'highpass')   #配置滤波器 8 表示滤波器的阶数
filtedData = signal.filtfilt(b, a, data)  #data为要过滤的信号

3).带通滤波

这里假设采样频率为1000hz,信号本身最大的频率为500hz，要滤除100hz以下，400hz以上频率成分，即截至频率为100，400hz,则wn1=2*100/1000=0.2，Wn1=0.2； wn2=2*400/1000=0.8，Wn2=0.8。Wn=[0.02,0.8]

from scipy import signal

b, a = signal.butter(8, [0.2,0.8], 'bandpass')   #配置滤波器 8 表示滤波器的阶数
filtedData = signal.filtfilt(b, a, data)  #data为要过滤的信号

4).带阻滤波

这里假设采样频率为1000hz,信号本身最大的频率为500hz，要滤除100hz以上，400hz以下频率成分，即截至频率为100，400hz,则wn1=2*100/1000=0.2，Wn1=0.2； wn2=2*400/1000=0.8，Wn2=0.8。Wn=[0.02,0.8]，和带通相似，但是带通是保留中间，而带阻是去除。

from scipy import signal

b, a = signal.butter(8, [0.2,0.8], 'bandstop')   #配置滤波器 8 表示滤波器的阶数
filtedData = signal.filtfilt(b, a, data)  #data为要过滤的信号

函数的介绍：

1、滤波函数

scipy.signal.filtfilt(b, a, x, axis=-1, padtype='odd', padlen=None, method='pad', irlen=None)

输入参数：

b: 滤波器的分子系数向量

a: 滤波器的分母系数向量

x: 要过滤的数据数组。（array型）

axis: 指定要过滤的数据数组x的轴

padtype: 必须是“奇数”、“偶数”、“常数”或“无”。这决定了用于过滤器应用的填充信号的扩展类型。{‘odd’, ‘even’, ‘constant’, None}

padlen：在应用滤波器之前在轴两端延伸X的元素数目。此值必须小于要滤波元素个数- 1。（int型或None）

method：确定处理信号边缘的方法。当method为“pad”时，填充信号；填充类型padtype和padlen决定，irlen被忽略。当method为“gust”时，使用古斯塔夫森方法，而忽略padtype和padlen。{“pad” ，“gust”}

irlen：当method为“gust”时，irlen指定滤波器的脉冲响应的长度。如果irlen是None，则脉冲响应的任何部分都被忽略。对于长信号，指定irlen可以显著改善滤波器的性能。（int型或None）

输出参数：

y:滤波后的数据数组

2、滤波器构造函数(Butterworth滤波器)

scipy.signal.butter(N, Wn, btype='low', analog=False, output='ba')

输入参数：

N:滤波器的阶数

Wn：归一化截止频率。计算公式Wn=2*截止频率/采样频率。（注意：根据采样定理，采样频率要大于两倍的信号本身最大的频率，才能还原信号。截止频率一定小于信号本身最大的频率，所以Wn一定在0和1之间）。当构造带通滤波器或者带阻滤波器时，Wn为长度为2的列表。

btype : 滤波器类型{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’},

output : 输出类型{‘ba’, ‘zpk’, ‘sos’},

输出参数：

b，a: IIR滤波器的分子（b）和分母（a）多项式系数向量。output='ba'

z,p,k: IIR滤波器传递函数的零点、极点和系统增益. output= 'zpk'

sos: IIR滤波器的二阶截面表示。output= 'sos'

1.txt  存放信号数据

代码实战：

from scipy import signal
import matplotlib.pyplot as pl
import numpy as np
#处理基线漂移
#scipy.signal.detrend(): 从信号中删除线性趋势：
# t = np.linspace(0,5,100)
# x = t + np.random.normal(size=100)
# print(x)
# pl.plot(t, x, linewidth=3)
# pl.plot(t, signal.detrend(x), linewidth=3)
# pl.show()

#读取信号数据
def readtxt(path):
    with open(path,'r') as f:
        str=f.readline()
        list = str.split(' ')
    list1=[];
    for i,x in enumerate(list):
        if ((i%5 == 0) or (i%5 == 1) or (i%5 == 2)) and x !='':
            list1.append(float(x))
    return list1
#处理基线漂移
def singnal(path):
    list=readtxt(path)
    print(len(list))
    #
    list3=[]
    list2=[]
    #切片从1000以后的数据开始计算
    for i,x in enumerate(list[38000::]):
        list2.append(float((i+1)*0.002))
        list3.append(x)
    #处理基线漂移
    list_jx=signal.detrend(list3)

    #巴特沃斯滤波器
    b, a = signal.butter(8, [0.2, 0.8], 'bandstop')  # 配置滤波器 8 表示滤波器的阶数
    # 信号进行滤波处理
    filtedData = signal.filtfilt(b, a, list_jx)  # data为要过滤的信号

    #图表绘制
    pl.plot(list2, list3, linewidth=1)
    pl.plot(list2,filtedData,linewidth=1)
    pl.show()


if __name__=="__main__":
    singnal('1.txt')

效果展示：

这个滤波和处理基线不是太明显。

参考地址：https://www.bookstack.cn/read/scipy-lecture-notes_cn/spilt.9.12356b8765f6ac60.md