【LSTM时序预测】基于matlab EMD结合LSTM风速数据预测【含Matlab源码 2051期】
⛄一、EMD-DELM简介
1 方法及原理
1.1 EMD基本原理
经验模态分解可基于数据本身,将复杂信号分解为一系列IMF和一个r(t),分解信号时,不需要预先设置任何基函数。因为这一特点,理论上EMD方法可预处理任何一种信号的数据,因此被广泛应用。
x(t)=∑fIMF,s+r(t) (1)
每个IMF分量都应满足以下2个特点:
(1)在整个时间范围内,局部极值点和过零点的数量必须相等或最多相差一个;
(2)在任何时间点,局部最大包络和局部最小包络的平均值必须为0。
IMF代表数据的固有振动模式。根据IMF的定义,IMF每个振动周期只有一个振动模式,不存在其他复杂波。作为混合序列的煤气消耗数据也可以分解为如式(1)所示的形式。分解后的IMF分量包含不同的局部特征信号。因此,利用EMD分解煤气消耗数据是可行的。
1.2 长短时记忆神经网络
LSTM在解决长时间序列相关性问题上具有独特优势,是深度学习中比较流行的方法。LSTM的内部结构由遗忘门、输入门、输出门和存储单元组成。由于其独特的“记忆”优势,LSTM网络得到了越来越广泛的应用。图1所示为LSTM的网络结构。
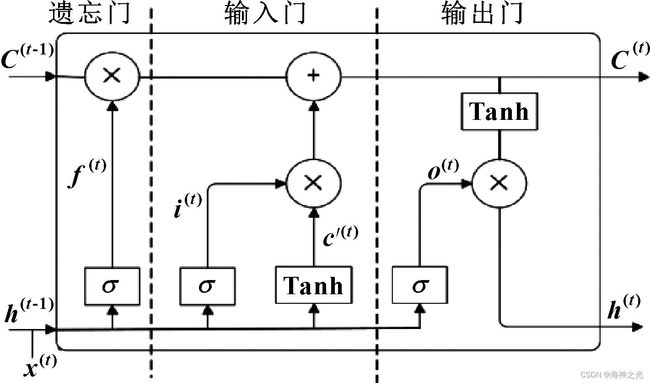
图1 LSTM结构
遗忘门决定了前一时刻的单元状态需要保留到当前时刻的程度。
f(t)=σ[Wfh(t-1)+Ufx(t)+bf] (2)
输入门分为两部分:Sigmoid层决定哪些信息需要更新,并输出为i(t);Tanh层创建候选向量c′(t)。最后,组合这2个向量来创建更新值。数学表达式为
i(t)=σ[Wih(t-1)+Uix(t)+bi] (3)
c′(t)=tanh[Wch(t-1)+Ucx(t)+bc] (4)
单元状态C(t)是遗忘门f(t)与上一时刻单元状态C(t-1)乘积和i(t)与a(t)乘积的和。
Ct=C(t-1)⨂f(t)+i(t)⨂a(t) (5)
输出门是输出到LSTM控制单元状态的当前输出值,由Sigmoid层和Tanh层两部分组成。
o(t)=σ[Woh(t-1)+Uox(t)+bo] (6)
h(t)=o(t)⨂tanh[C(t)] (7)
其中:σ为激活函数;Wf、Wi、Wc、Wo、Uf、Ui、Uc、Uo为权重;h(t-1)为前一个神经元的输出结果;bf、bi、bc、bo为偏置;⨂为元素乘法符号。
由于Tanh的导数大于Sigmoid函数的导数,Tanh激活函数通常用于解决RNN梯度消失问题。Sigmoid函数估计输入数据与先前隐藏状态的权重和激活,值在0~1之间,指示允许流入多少相关信息。各个门之间以特定的关系相互作用、过滤和保存信息。这种结构可以有效解决梯度消失问题。
⛄二、部分源代码
clc;clear;close all
%%
lstm=load(‘结果/lstm.mat’);%1
emd_lstm=load(‘结果/emd_lstm.mat’);%2
%% 1
disp(‘1-结果分析-lstm’)
result(lstm.true_value,lstm.predict_value)
fprintf(‘\n’)
%% 2
disp(‘2-结果分析-emd-lstm’)
result(emd_lstm.true_value,emd_lstm.predict_value)
fprintf(‘\n’)
%% 画图
figure
plot(lstm.true_value)
hold on;grid on
plot(lstm.predict_value)
plot(emd_lstm.predict_value)
legend(‘真实值’,‘lstm预测值’,‘emd-lstm预测值’)
title(‘各算法预测效果对比’)
ylabel(‘值’)
xlabel(‘测试集样本’)
⛄三、运行结果
⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]翟慧,熊伟,李福进,杨杰.基于EMD-LSTM的冷轧煤气消耗量预测模型仿真[J].机床与液压. 2022,50(14)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
