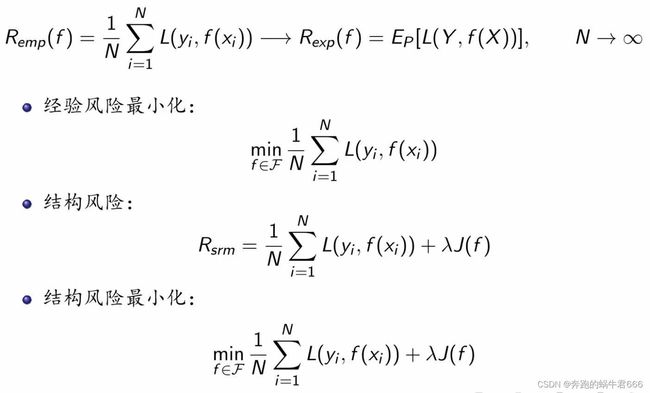统计学习方法 | 概论

一.简介

统计学习是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科

1.统计学习方法的步骤

①得到一个有限的训练数据集合

②确定学习模型的集合（模型）

③确定模型选择的准则（策略）

④实现求解最优模型的算法（算法）

⑤通过学习方法选择最优模型

⑥利用学习的最优模型对新数据进行预测或分析

2.统计学习方法的分类

基本分类：监督学习，无监督学习，强化学习

按模型分类：概率 / 非概率模型 ，线性 / 非线性模型，参数化 / 非参数化模型

按算法分类：在线学习，批量学习

按技巧分类：贝叶斯学习，核方法

3.监督学习

定义：指从标注数据中学习预测模型的机器学习问题，其本质是学习输入到输出的映射的统计规律

根据变量类型不同：

输入变量与输出变量均为连续变量的预测问题：回归问题

输出变量为有限个离散变量的预测问题：分类问题

输入变量与输出变量均为变量序列的预测问题：标注问题

4.无监督学习

定义：指从无标注数据中学习预测模型的机器学习问题，其本质是学习数据中的统计规律或潜在结构

二.统计学习方法的三要素

统计学习方法 = 模型 + 策略 + 算法

1.模型

假设空间：所有可能的条件概率分布或决策函数，用F表示

 

2.策略

3.算法

算法：如何求解最优模型的问题

若优化问题存在显式解析解，算法简易

通常不存在解析解，需要数值计算方法，比如梯度下降法

三.模型的评估与选择

过拟合：学习所得模型包含参数过多，出现对已知数据预测很好，但对未知数据预测很差的现象

四.正则化与交叉验证 

正则化：实现结构风险最小化策略

奥卡姆剃刀原理：在模型选择中，选择所有可能模型中，能很好解释已知数据并且十分简单的模型

数据充足的情况下，数据集分为：训练集，验证集，测试集

训练集（training set）：用以训练模型

验证集（validation set）：用以选择模型

测试集（test set）：用以最终对学习方法的评估

数据不充足的情况下：

简单交叉验证：随机将数据分为两部分，即训练集和测试集

S折交叉验证：随机将数据分为S个互不相交，大小相同的子集，其中S-1个子集作为训练集，余下的子集作为测试集

留一交叉验证：S折交叉验证的特殊情形，S=N

五.泛化能力

1.泛化误差

2.泛化误差上界

定义

指泛化误差的概率上界。两种学习方法的优劣，通常通过它们的泛化误差上界进行比较

性质

样本容量的函数：当样本容量增加时，泛化上界趋于0

假设空间容量的函数：假设空间容量越大，模型就越难学，泛化误差上界就越大

考虑如下二分类问题

3.Hoeffding不等式

六.生成模型与判别模型 

1.生成模型

定义：由数据学习联合分布概率P(X,Y)，然后求出P(Y|X)作为预测模型，即P(Y|X)=P(X,Y)/P(X)

例：朴素贝叶斯法，隐马尔可夫模型

注：输入和输出变量要求为随机变量

2.判别模型

定义：由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测模型

例：k近邻法，感知机，决策树

注：不需要输入和输出变量均为随机变量

七.监督学习的应用 

1.分类问题

评价指标

分类准确率

方法

感知机，k近邻法，朴素贝叶斯，决策树，logistic回归

应用

银行业务，网络安全，图像处理，手写识别，互联网搜索

2.标注问题

方法

隐马尔可夫模型，条件随机场

应用

信息抽取，自然语言处理

3.回归问题

类型

按输入变量个数：一元回归，多元回归

按输入和输出变量之间关系：线性回归，非线性回归

损失函数

平方损失

应用

商务领域

八.Python实现

1.使用最小二乘法拟和曲线

# 目标函数
def real_func(x):
    return np.sin(2*np.pi*x)

# 多项式
def fit_func(p, x):
    f = np.poly1d(p)
    return f(x)

# 残差
def residuals_func(p, x, y):
    ret = fit_func(p, x) - y
    return ret

# 十个点
x = np.linspace(0, 1, 10)
x_points = np.linspace(0, 1, 1000)
# 加上正态分布噪音的目标函数的值
y_ = real_func(x)
y = [np.random.normal(0, 0.1) + y1 for y1 in y_]


def fitting(M=0):
    """
    M    为 多项式的次数
    """
    # 随机初始化多项式参数
    p_init = np.random.rand(M + 1)
    # 最小二乘法
    p_lsq = leastsq(residuals_func, p_init, args=(x, y))
    print('Fitting Parameters:', p_lsq[0])

    # 可视化
    plt.plot(x_points, real_func(x_points), label='real')
    plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')
    plt.plot(x, y, 'bo', label='noise')
    plt.legend()
    return p_lsq

# M=9
p_lsq_9 = fitting(M=9)

 

当M=9时，多项式曲线通过了每个数据点，但是造成了过拟合

2.正则化

regularization = 0.0001


def residuals_func_regularization(p, x, y):
    ret = fit_func(p, x) - y
    ret = np.append(ret,
                    np.sqrt(0.5 * regularization * np.square(p)))  # L2范数作为正则化项
    return ret

# 最小二乘法,加正则化项
p_init = np.random.rand(9 + 1)
p_lsq_regularization = leastsq(
    residuals_func_regularization, p_init, args=(x, y))

plt.plot(x_points, real_func(x_points), label='real')
plt.plot(x_points, fit_func(p_lsq_9[0], x_points), label='fitted curve')
plt.plot(
    x_points,
    fit_func(p_lsq_regularization[0], x_points),
    label='regularization')
plt.plot(x, y, 'bo', label='noise')
plt.legend()