CH7 逻辑回归

CH7 逻辑回归

属于机器学习中的监督学习，主要用来解决二分类问题。

通过给定的n组数据（训练集）来训练模型，并在训练结束后对给定的一组或多组数据（测试集）进行分类。其中每一组数据都是由p 个指标构成。

逻辑回归是用来分类的。例如，我们给出一个人的 [身高，体重] 这两个指标，然后判断这个人是属于”胖“还是”瘦“这一类。对于这个问题，我们可以先测量n个人的身高、体重以及对应的指标”胖“,"瘦”，把胖和瘦分别用0和1来表示，把这n组数据输入模型进行训练。训练之后再把待分类的一个人的身高、体重输入模型中，看这个人是属于“胖”还是“瘦”。

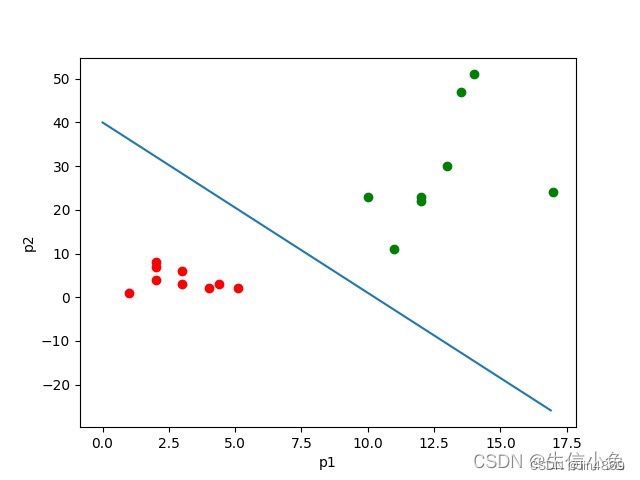
从本质上来说，逻辑回归训练后的模型是平面的一条直线（p=2),或是平面（p=3)，超平面（p>3)。并且这条线或平面把空间中的散点分成两半，属于同一类的数据大多数分布在曲线或平面的同一侧。

7.1 算法原理

处理二分类问题，其中一类标签为0，另一类为1。我们需要一个函数，对于输入的每一组数据$x^{(i)}$，都能映射成0～1之间的数，并且如果函数值大于0.5，就判定属于1，否则属于0。

7.1.1 预测函数推导过程

函数中需要待定参数，通过利用样本训练，使得这个参数能够对训练集中的数据有很准确的预测。这个函数就是sigmoid函数
$$\sigma (x)=\frac{1}{1+e^{-x}}$$

在这里我们设函数为
$$h(x^i)=\frac{1}{1+e^{-(w^T{x}^i+b)}}$$
这里$x^i$是测试集第i个数据，是p维列向量$(x_1^i{x}_2^i\dots x_p^i{)}^T$
$w$是p维列向量，$(w_1{w}_2\dots w_p{)}^T$，为待求参数
b是一个数，也是待求参数

对于$w^{T}x+b$，其结果是$w_1{x}_1+w_2{x}_2+\cdots +w_p{x}_p+b$
所以把$w$写成$(w_1{w}_2\dots w_{p}b{)}^T$， $x^i$写成$(x_1^i{x}_2^i\dots x_p^{i}1{)}^T$， $w^{T}x+b$就可以写成$w^T+x$，则最终预测函数为：
$$h(x^i)=\frac{1}{1+e^{-w^T{x}^i}}$$

7.2 求解参数(证明题)

7.2.1 极大似然估计

思想是，一个事件发生了，那么发生这个事件的概率就是最大的。

对于样本i，其类别为$y_i\in (0,1)$。对于样本i，可以把$h(x_i)$看成一种概率。$y_i$对应是1是，概率是$h(x_i)$，即$x_i$属于1的可能性；$y_i$对应是0时，概率是$1-h(x_i)$，即$x_i$属于0的可能性。构造极大似然函数：
$$\prod _{i=1}^{i=k}h(x_i)\prod _{i=k+1}^n(1-h(x_i))$$

其中i从0到k是属于类别1的个数k，从k+1到n是属于类别0的个数n-k。由于y是标签0或1，所以上式也可以写成：
$$\prod _{i=1}^{n}h(x_i{)}^{y_i}(1-h(x_i){)}^{1-y_i}$$

为了方便我们对式子取对数。因为是求式子的最大值，所以转换成式子乘负1然后求最小值。可得：
$$-\sum _{i=1}^n{y}_{i}ln(h(x_i))-(1-y_i)ln(1-h(x_i))$$

7.2.2 损失函数

同时对于n个数据，累加后值会很大，之后如果用梯度下降容易导致梯度爆炸，所以除以样本总数n，得到的为损失函数：
$$L(w)=\frac{1}{n}(\sum _{i=1}^n-y_{i}ln(h(x_i))-(1-y_i)ln(1-h(x_i)))$$
损失函数是参数$w$的函数

总的损失函数可以用来评价模型的好坏，损失函数越小越说明模型和参数越符合训练样本。

7.2.3 梯度下降法求最小值

即求损失函数的导数
$$L(w)=\frac{1}{n}(\sum _{i=1}^n-y_{i}ln(h(x_i))-(1-y_i)ln(1-h(x_i)))$$
$$\frac{\partial L(w)}{\partial w}=\frac{1}{n}(\sum _{i=1}^n(-y_i\frac{1}{h(x_i)}\cdot \frac{\partial h(x_i)}{\partial w})+(1-y_i)\frac{1}{1-h(x_i)}\cdot \frac{\partial h(x_i)}{\partial w})$$

---

$$记：\sigma (x)=\frac{1}{1+e^{-x}}$$
$$\sigma (w^T)=\frac{1}{1+e^{-w^{T}x}}=h(x)$$
$${\sigma }^{\prime }(x)=\sigma (x)(1-\sigma (x))$$

---

$$\begin{array}{rl}\frac{\partial h(x_i)}{\partial w}& =\frac{\partial \frac{1}{1+e^{-w{x}_i}}}{\partial w}=\frac{\partial (\sigma (w^T{x}_i))}{\partial w^T{x}_i}\\ & =\sigma (w^{T}x)(1-\sigma (w^{T}x))\cdot \frac{\partial w^T{x}_i}{\partial w}\\ & =\sigma (w^{T}x)(1-\sigma (w^{T}x))x_i\end{array}$$

---

$$\begin{array}{rl}d(tr(w^{T}x))& =tr(d{w}^T)\\ & =tr(x\cdot d{w}^T)\\ & \Rightarrow \frac{\partial w^{T}x}{\partial w}=x\text{对上一步求导的解释}\end{array}$$

---

$$\begin{array}{rl}\frac{\partial L(w)}{\partial w}& =\frac{1}{n}(\sum _{i=1}^n-y_i\frac{1}{\sigma (w^{T}x)}\sigma (w^{T}x)(1-\sigma (w^{T}x)x_i)+(1-y_i)\frac{1}{\sigma (w^{T}x)}\cdot \sigma (w^{T}x)(1-\sigma (w^{T}x))x_i)\\ & =\frac{1}{n}(\sum _{i=1}^n-y_i(1-\sigma (w^T{x}_i))x_i+y(1-y_i)\sigma (w^T{x}_i)x_i)\\ & =\frac{1}{n}(\sum _{i=1}^n-y_i{x}_x+y_i\sigma (w^T{x}_i)x_i-y_i\sigma (w^T{x}_i)x_i+\sigma (w^T{x}_i)x_i)\\ & =\frac{1}{n}(\sum _{i=1}^n-y_i{x}_i+\sigma (w^T{x}_i)x_i)\\ & =\frac{1}{n}(\sum _{i=1}^n(\sigma (w^T{x}_i)-y_i)x_i)\end{array}$$