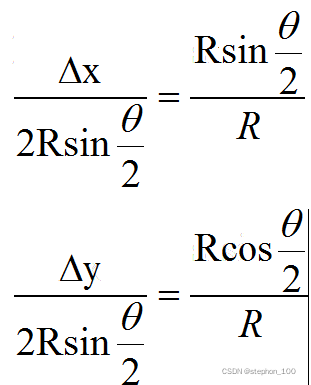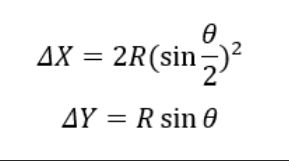Halcon九点及旋转标定流程

 

参考文章：剖析Halcon 9点标定旋转中心标定与使用_william9987的博客-CSDN博客_halcon旋转标定

 

一、XY轴九点标定：

使用仿射变换：

夹具夹取产品或者标定块，选取一个特征，开始进行标定

X轴、Y轴移动一个位置，记录轴的物理坐标：（Qx1，Qy1）

提取图像中对应特征点，图像像素坐标：（Px1，Py1）

运动第N位置，记录下点位轴轴坐标（QxN，QyN），t提取像素坐标：（PxN，PyN）

使用vector_to_hom_mat2d （Px， Py， Qx ， Qy， HomMat2D）得到图像坐标和世界坐标的转换关系矩阵。这种简单的标定方法不能消除镜头和相机畸变。

 

*创建空数组用来存放模板在图像坐标系的位置
ImageXPix:=[]
ImageYPix:=[]
*****************************
*确定好相机移动的九个物理坐标数组
WorldX:=[8,8,8,0,0,0,-8,-8,-8]
WorldY:=[-8,0,8,8,0,-8,-8,0,8]

*开始标定
i:=0
* 打开相机
open_framegrabber ('GigEVision', 0, 0, 0, 0, 0, 0, 'default', -1, 'default', -1, 'false', 'default', 'ccd1', 0, -1, AcqHandle)
grab_image_start (AcqHandle, -1)
*采集图像  获取9个像素坐标
for i:=1 to 9 by 1   
     grab_image (Image, AcqHandle) 
    *用第一张图片创建模板
    if(i=1)
        disp_message(3600, '创建模板区域，右键确定', 'window', 12, 12, 'red', 'false')
        draw_region(Region, 3600)
        reduce_domain(Image, Region, ImageReduced)
        create_shape_model(ImageReduced, 'auto', rad(-180), rad(360), 'auto', 'auto', 'use_polarity', 'auto', 'auto', ModelID)        
    endif

    find_shape_model(Image, ModelID,  rad(-180), rad(360), 0.5, 1, 0.5, 'least_squares', 0, 0.9, Row, Column, Angle, Score)
    if(|Row|>0)
       dev_display_shape_matching_results(ModelID, 'red', Row, Column, Angle, 1, 1, 0)
        *将位置添加到数组
       ImageXPix:=[ImageXPix,Column]
       ImageYPix:=[ImageYPix,Row]
    else
        disp_message(3600, '模板创建失败', 'window', 30, 12, 'red', 'false')      
    endif
    stop()  
endfor
close_framegrabber (AcqHandle)
*计算对应点的仿射变换矩阵
vector_to_hom_mat2d(ImageYPix, ImageXPix, WorldY, WorldX, HomMat2D)
******************
*保存和读取标定好的仿射矩阵
write_tuple (HomMat2D, 'C:/Users/LZj/Desktop/hm.tup')
read_tuple ('C:/Users/LZj/Desktop/hm.tup', HomMat2D)

***********应用*************
*打开串口，与运动程序通讯
open_serial ('COM2', SerialHandle)
*close_serial(SerialHandle)
set_serial_param (SerialHandle, 9600, 8, 'none', 'none', 1, 1000, 'unchanged')
i:=0
open_framegrabber ('GigEVision', 0, 0, 0, 0, 0, 0, 'default', -1, 'default', -1, 'false', 'default', 'ccd1', 0, -1, AcqHandle)
grab_image_start (AcqHandle, -1)
while(true)
   grab_image (Image, AcqHandle)
   get_image_size(Image, Width, Height)
   if(i=0)
       i:=1
       draw_region(Region1, 3600)
       reduce_domain(Image, Region1, ImageReduced1)
       create_shape_model(ImageReduced1, 'auto', rad(-180), rad(360), 'auto', 'auto', 'use_polarity', 'auto', 'auto', ModelID)       
   endif
   find_shape_model(Image, ModelID, rad(-180), rad(360), 0.5, 1, 0.5, 'least_squares', 0, 0.9, Row, Column, Angle, Score)
   if(Score>0)       
        dev_display_shape_matching_results (ModelID, 'red', Row, Column, Angle, 1, 1, 0)         
        *将图像中心的像素坐标仿射得到物理坐标Qy1, Qx1
        affine_trans_point_2d (HomMat2D, Height/2-1, Width/2-1, Qy1, Qx1)
        *将找到的模板中心的像素坐标仿射得到物理坐标Qy2, Qx2
        affine_trans_point_2d (HomMat2D,  Row, Column, Qy2, Qx2)       
        *求出相机中心和模板中心之间的物理距离差
        string_send:='go2:'+(Qx1-Qx2)+','+(Qy1-Qy2)+',0'
        *将这个物理距离差通过串口发送给运动控制程序，让相机中心移动到模板的中心位置
        write_serial (SerialHandle, ords(string_send))
        try
            while(1)  
                *获得鼠标的能力  1表示鼠标左键  4表示鼠标右键               
                get_mbutton (3600, Row3, Column3, Button)
                if(Button=1)
                    grab_image (Image, AcqHandle)
                    find_shape_model (Image, ModelID, -0.39, 0.78, 0.5, 1, 0.5, 'least_squares', 0, 0.9, Row, Column, Angle, Score)
                    if(Score>0)                           
                        dev_display (Image)
                        dev_set_color ('green')
                        gen_cross_contour_xld (Cross1, Height/2-1, Width/2-1, 6, 0)
                        dev_set_color ('red')
                        gen_cross_contour_xld (Cross,  Row, Column, 15,rad(45))
                        *验证相机中心和模板中心是否基本重合
                        affine_trans_point_2d (HomMat2D,  Row, Column, Qy2, Qx2)
                        string_send:='go2:'+(Qx1-Qx2)+','+(Qy1-Qy2)+',0'
                        disp_message (3600, string_send, 'window', 12, 12, 'black', 'true')
                    endif
                endif               
                if(Button=4)
                    break
                endif
            endwhile
        catch (Exception)                     
        endtry
    endif   
endwhile
     

 

二、旋转轴标定：

 参考一、http://www.elecfans.com/d/1601708.html

 参考二、http://t.csdn.cn/fZgi9

1、相机固定，物体在轴上旋转

 

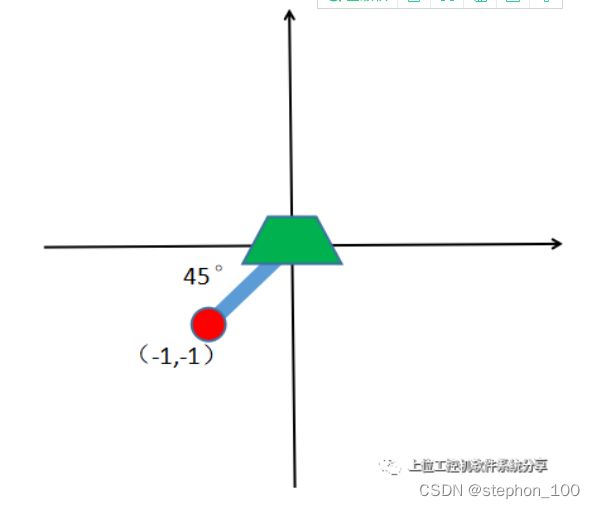
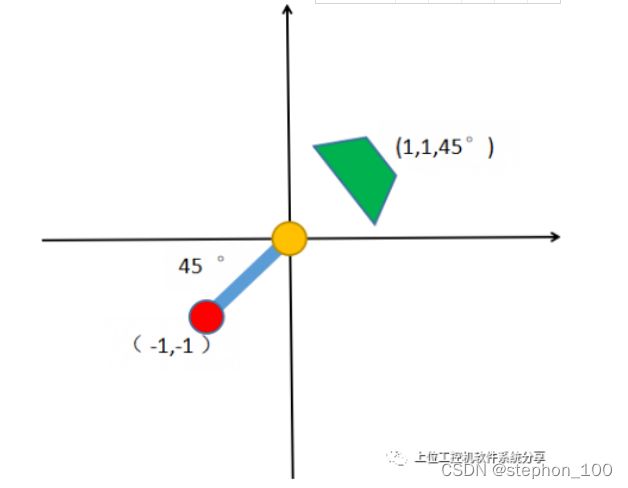
红点为目标物体的旋转中心，物体的标准基准取料位置为图左位置，实际取料位置为右图。相比基准位置偏移XYR（1,1,45°）

 先把XY方向补偿了，只观察旋转轴的旋转过程就可以了。上图是旋转前。

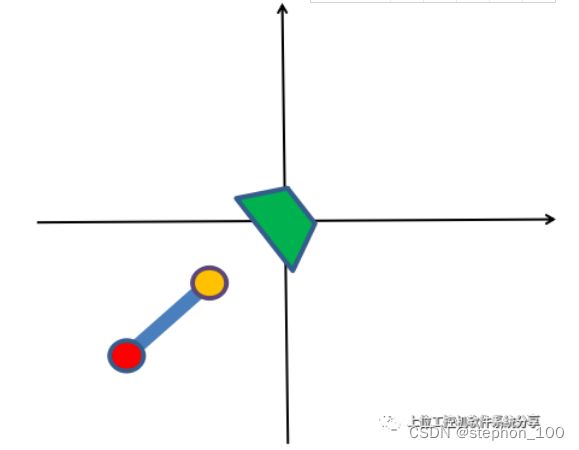
旋转后：

                                ​​​​​​​        

 

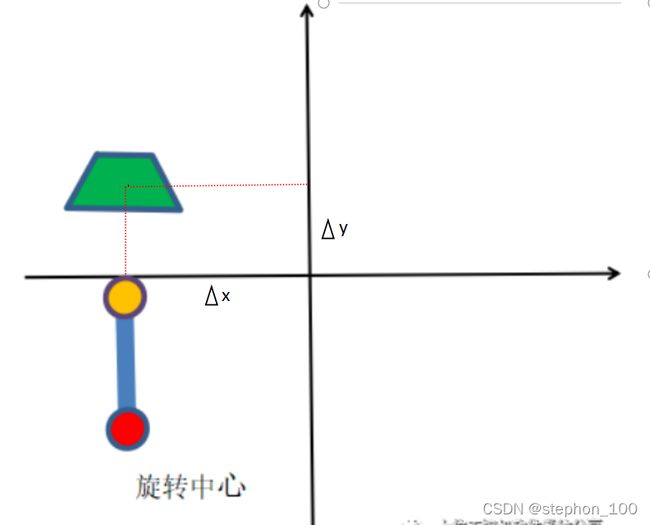
 可以看到按旋转中心转正物体角度后会产生一个∆x和∆y的偏移。

只要算出来∆x和∆y，加上之前的xy的偏移就可以实现定位纠偏了。

 

在相机定位做补偿的流程中，我们的已知条件是：

1、当前物体的特征中心点（图2）。2、标定时拍照的特征中心点，作为基准点（图1）

通过抓边知道：3、当前物体的倾斜角度（图2）。4、标定的基准角度（图1）。

5、物体的旋转中心（通过旋转标定获取）。

以上已知条件中1、3是当前物体拍照获得的。2、4、5是标定流程中获得。旋转标定的目的主要就是得到条件5、旋转中心。

有了旋转中心和偏移角度（条件3-条件2），以及物体实际的位置（条件1）就可以算出将物体按旋转中心转正角度后xy方向上的偏移∆x和∆y。再加上xy的偏移就实现了定位补偿。

通过轴旋转多个角度在图像坐标系上获得多个点，使用halcon算子拟合圆得到旋转中心坐标的旋转半径R。

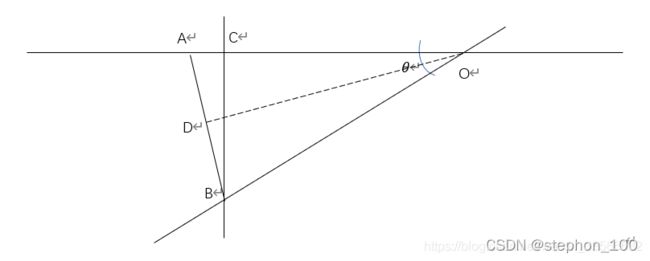
∆x和∆y的计算公式：

 如图：通过标定旋转中心O坐标和旋转半径R已知。旋转角度需要补偿θ已知，求∆x=AC，∆y=BC。

因为三角形ABC和三角形AOD是相似三角形，所以有：

                                

 这样就计算出了旋转后的∆x和∆y偏移，也就实现了补偿。