因果推理(七):Unobserved Confounding: Bounds and Sensitivity Analysis
上一章的估计过程的一个前提是我们掌握了去混杂的充分调整集。也就是说,我们确定W是一个充分调整集的时候,我们可以用下面的公式计算因果量。

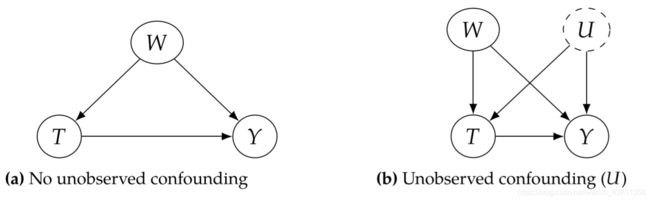
然而,很多时候,可能会存在没有被我们观测到的混杂因素,比如上图中的U。在这种情况下,我们需要同时对W和U进行调整,但由于我们没有观察到U,势必不会调整U,这就使得我们的估计结果产生了误差。这一章,我们将探讨这个误差的大小及其对整个结果的影响。

1. Bounds
在因果推理中,我们定义了一个很强的假设“Unconfoundness”,满足unconfoundness,我们就可以对因果量进行精确的无偏估计。然而,在现实中一般会存在unobserved confounding,这使得我们的unconfoundnessJ假设过强了。为此,我们可以定义一个较弱的假设,然后得到的估计结果会是一个区间。

No-Assumptions Bound
假设潜在结果的取值为 a a a到 b b b之间,则个体干预效应和平均干预效应的取值都在 a − b a-b a−b和 b − a b-a b−a之间。即下图的边界潜在结果假设成立时,下面两式子成立。

a − b ≤ Y i ( 1 ) − Y i ( 0 ) ≤ b − a a-b \leq Y_{i}(1)-Y_{i}(0) \leq b-a a−b≤Yi(1)−Yi(0)≤b−a
a − b ≤ E [ Y ( 1 ) − Y ( 0 ) ] ≤ b − a a-b \leq \mathbb{E}[Y(1)-Y(0)] \leq b-a a−b≤E[Y(1)−Y(0)]≤b−a
上式中ITE和ATE的边界的长度均为 2 ( b − a ) 2(b-a) 2(b−a)(这个长度被称为 trivial length)。然而,神奇的是,对于ATE,我们可以将其长度减半。
ATE的公式可以写成下面这样:
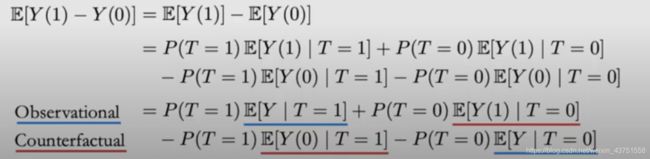
在上面的式子中,蓝色表示的是观察变量,红色标注的是反事实变量。我们将上式称为观察-反事实分解(observational-counterfactual decomposition)。令 π ≜ P ( T = 1 ) \pi \triangleq P(T=1) π≜P(T=1),可以将观察-反事实分解表示为下式:
E [ Y ( 1 ) − Y ( 0 ) ] = π E [ Y ∣ T = 1 ] + ( 1 − π ) E [ Y ( 1 ) ∣ T = 0 ] − π E [ Y ( 0 ) ∣ T = 1 ] − ( 1 − π ) E [ Y ∣ T = 0 ] \begin{aligned} \mathbb{E}[Y(1)-Y(0)]=& \pi \mathbb{E}[Y \mid T=1]+(1-\pi) \mathbb{E}[Y(1) \mid T=0] \\ &-\pi \mathbb{E}[Y(0) \mid T=1]-(1-\pi) \mathbb{E}[Y \mid T=0] \end{aligned} E[Y(1)−Y(0)]=πE[Y∣T=1]+(1−π)E[Y(1)∣T=0]−πE[Y(0)∣T=1]−(1−π)E[Y∣T=0]
因为Y的取值是a到b,所以对于上式中可以观察到的变量 E [ Y ∣ T = 1 ] E[Y|T=1] E[Y∣T=1]和 E [ Y ∣ T = 0 ] E[Y|T=0] E[Y∣T=0],其取值为a到b,而对于反事实变量,在没有任何假设的情况下,我们不能确定他的取值范围。因此,有
E [ Y ( 1 ) − Y ( 0 ) ] ≤ π E [ Y ∣ T = 1 ] + ( 1 − π ) b − π a − ( 1 − π ) E [ Y ∣ T = 0 ] \mathbb{E}[Y(1)-Y(0)] \leq \pi \mathbb{E}[Y \mid T=1]+(1-\pi) b-\pi a-(1-\pi) \mathbb{E}[Y \mid T=0] E[Y(1)−Y(0)]≤πE[Y∣T=1]+(1−π)b−πa−(1−π)E[Y∣T=0]
E [ Y ( 1 ) − Y ( 0 ) ] ≥ π E [ Y ∣ T = 1 ] + ( 1 − π ) a − π b − ( 1 − π ) E [ Y ∣ T = 0 ] \mathbb{E}[Y(1)-Y(0)] \geq \pi \mathbb{E}[Y \mid T=1]+(1-\pi) a-\pi b-(1-\pi) \mathbb{E}[Y \mid T=0] E[Y(1)−Y(0)]≥πE[Y∣T=1]+(1−π)a−πb−(1−π)E[Y∣T=0]
于是, E [ Y ( 1 ) − Y ( 0 ) ] \mathbb{E}[Y(1)-Y(0)] E[Y(1)−Y(0)]的边界长度为上面两个不等式的右值相减,其结果为 b − a b-a b−a,也就是说,无假设边界长度为 b − a b-a b−a。

下图是一个例子:

无假设边界对应的间隔是中包含0,这意味着我们不能用它来判断有因果效应还是没有因果效应。
上述假设潜在实验结果 Y ( 1 ) Y(1) Y(1)和潜在对照结果 Y ( 0 ) Y(0) Y(0)的取值都在 a a a到 b b b之间,当潜在实验结果和潜在对照结果的取值范围不一致时,也可以按照上述方法得出ATE边界间隔长度。
Monotone Treatment Response(MTR)
假设干预总是有用,也就是说:
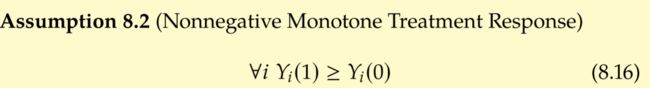
那么, E [ Y ( 1 ) ∣ T = 0 ] ≥ E [ Y ∣ T = 0 ] E[Y(1)|T=0]\geq{E[Y|T=0]} E[Y(1)∣T=0]≥E[Y∣T=0], E [ Y ( 0 ) ∣ T = 1 ] ≤ E [ Y ∣ T = 1 ] E[Y(0)|T=1]\leq{E[Y|T=1]} E[Y(0)∣T=1]≤E[Y∣T=1],于是有,
E [ Y ( 1 ) − Y ( 0 ) ] = π E [ Y ∣ T = 1 ] + ( 1 − π ) E [ Y ( 1 ) ∣ T = 0 ] − π E [ Y ( 0 ) ∣ T = 1 ] − ( 1 − π ) E [ Y ∣ T = 0 ] ≥ π E [ Y ∣ T = 1 ] + ( 1 − π ) E [ Y ∣ T = 0 ] − π E [ Y ∣ T = 1 ] − ( 1 − π ) E [ Y ∣ T = 0 ] = 0 \begin{aligned} \mathbb{E}[Y(1)-Y(0)]=& \pi \mathbb{E}[Y \mid T=1]+(1-\pi) \mathbb{E}[Y(1) \mid T=0] \\ &-\pi \mathbb{E}[Y(0) \mid T=1]-(1-\pi) \mathbb{E}[Y \mid T=0] \\ \mathbb \geq & \pi \mathbb{E}[Y \mid T=1]+(1-\pi) \mathbb{E}[Y \mid T=0] \\ &-\pi \mathbb{E}[Y \mid T=1]-(1-\pi) \mathbb{E}[Y \mid T=0] \\ =& 0 \end{aligned} E[Y(1)−Y(0)]=≥=πE[Y∣T=1]+(1−π)E[Y(1)∣T=0]−πE[Y(0)∣T=1]−(1−π)E[Y∣T=0]πE[Y∣T=1]+(1−π)E[Y∣T=0]−πE[Y∣T=1]−(1−π)E[Y∣T=0]0
于是得到非负MRT下界(Nonnegative MTR Lower Bound):

将非负MRT假设用到上面的例子上,可以将ATE的间隔缩小:

上面介绍的是非负MTR,下面介绍非正MTR。
假设treatment总是产生负面影响(例如枪伤对于活着),也就是:

此时得到非正MTR上界(Nonpositive MTRUpper Bound):

此时例子的ATE间隔变为:

Monotone Treatment Selection (MTS)
MTS是假设干预组的潜在结果好于控制组的潜在结果:

可以将这是为一种积极的自我选择,那些通常获得较好结局的患者会自行选择治疗组。
在这种假设下,我们可以得到MTS上界:

证明:
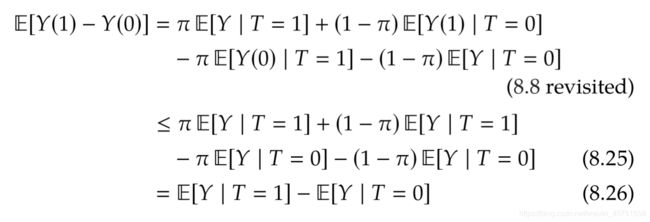
将MTS上界运用到例子中:

Optimal Treatment Selection (OTS)
最佳干预选择假设是说:对于干预组,潜在实验结果优于潜在对照结果;对于控制组,潜在对照结果优于潜在实验结果。即下图所述。

根据上述OTS假设,我们可以得到,
E [ Y ( 0 ) ∣ T = 1 ] ≤ E [ Y ( 1 ) ∣ T = 1 ] = E [ Y ∣ T = 1 ] E[Y(0)|T=1] \leq{E[Y(1)|T=1]} = E[Y|T=1] E[Y(0)∣T=1]≤E[Y(1)∣T=1]=E[Y∣T=1]
E [ Y ( 1 ) ∣ T = 0 ] ≤ E [ Y ( 0 ) ∣ T = 0 ] = E [ Y ∣ T = 0 ] E[Y(1)|T=0] \leq{E[Y(0)|T=0]} = E[Y|T=0] E[Y(1)∣T=0]≤E[Y(0)∣T=0]=E[Y∣T=0]
用 E [ Y ( 1 ) ∣ T = 0 ] E[Y(1)|T=0] E[Y(1)∣T=0]的上边界 E [ Y ∣ T = 0 ] E[Y|T=0] E[Y∣T=0]和 − E [ Y ( 1 ) ∣ T = 0 ] -E[Y(1)|T=0] −E[Y(1)∣T=0]的上边界 − a -a −a,我们可以计算得到ATE的上边界:

同样,可以得到ATE的下边界:

OTS边界:

例子:

在上面的例子中,仅仅有潜在结果取值限制(0-1)的时候,我们得到的ATE区间为[-0.17, 0.83],区间长度为1。加入非负MTR假设,ATE区间为[0, 0.83],非正MTR假设下ATE区间为[-0.17, 0]。在MTS假设下,ATE区间为[0, 0.7],区间长度为0.7。OTS假设下,ATE区间为[-0.14, 0.27],区间长度为0.41。虽然OTS假设的限制缩短了ATE区间长度,但是0仍然在其区间中。
利用OTS假设,我们不仅可以得到 E [ Y ( 1 ) ∣ T = 0 ] ≤ E [ Y ∣ T = 0 ] E[Y(1)|T=0] \leq E[Y|T=0] E[Y(1)∣T=0]≤E[Y∣T=0],我们还可以得到 E [ Y ( 1 ) ∣ T = 0 ] ≤ E [ Y ∣ T = 1 ] E[Y(1)|T=0] \leq E[Y|T=1] E[Y(1)∣T=0]≤E[Y∣T=1]。证明如下:
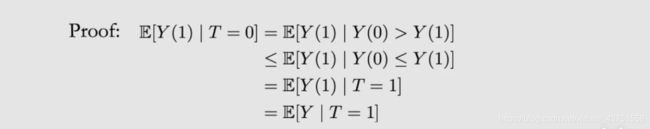
于是,
E [ Y ( 1 ) − Y ( 0 ) ] = π E [ Y ∣ T = 1 ] + ( 1 − π ) E [ Y ( 1 ) ∣ T = 0 ] − π E [ Y ( 0 ) ∣ T = 1 ] − ( 1 − π ) E [ Y ∣ T = 0 ] ≤ π E [ Y ∣ T = 1 ] + ( 1 − π ) E [ Y ∣ T = 1 ] − π a − ( 1 − π ) E [ Y ∣ T = 0 ] = E [ Y ( 1 ) ∣ T = 0 ] − π a − ( 1 − π ) E [ Y ∣ T = 0 ] \begin{aligned} \mathbb{E}[Y(1)-Y(0)]=& \pi \mathbb{E}[Y \mid T=1]+(1-\pi) \mathbb{E}[Y(1) \mid T=0] \\ &-\pi \mathbb{E}[Y(0) \mid T=1]-(1-\pi) \mathbb{E}[Y \mid T=0] \\ \leq & \pi \mathbb{E}[Y \mid T=1]+(1-\pi) \mathbb{E}[Y \mid T=1] \\ &-\pi a-(1-\pi) \mathbb{E}[Y \mid T=0] \\ =& \mathbb{E}[Y(1) \mid T=0]-\pi a-(1-\pi) \mathbb{E}[Y \mid T=0] \end{aligned} E[Y(1)−Y(0)]=≤=πE[Y∣T=1]+(1−π)E[Y(1)∣T=0]−πE[Y(0)∣T=1]−(1−π)E[Y∣T=0]πE[Y∣T=1]+(1−π)E[Y∣T=1]−πa−(1−π)E[Y∣T=0]E[Y(1)∣T=0]−πa−(1−π)E[Y∣T=0]
同样的,我们可以得到
E [ Y ( 1 ) − Y ( 0 ) ] ≥ π E [ Y ∣ T = 1 ] + ( 1 − π ) a − E [ Y ∣ T = 0 ] \mathbb{E}[Y(1)-Y(0)] \geq \pi \mathbb{E}[Y \mid T=1]+(1-\pi) a-\mathbb{E}[Y \mid T=0] E[Y(1)−Y(0)]≥πE[Y∣T=1]+(1−π)a−E[Y∣T=0]
于是,我们得到OST边界2:

将例子应用到OST边界2:

用这种假设方法得到的ATE区间虽然间隔长度比OTS1边界的间隔大,但是它的区间中不包含0,也就是说它识别了ATE(identify the sign of the effect)。【包含0意味着什么??】
因为OTS Bound 1 和OTS Bound 2 都是基于同样的假设,因此对于上面的例子,我们可以将两个区间合并,得到ATE的范围为:
0.07 ≤ E [ Y ( 1 ) − Y ( 0 ) ] ≤ 0.27 0.07 \leq \mathbb{E}[Y(1)-Y(0)] \leq 0.27 0.07≤E[Y(1)−Y(0)]≤0.27
这样就得到了一个可以identify the sign的更小区间。
综上,越强的假设会带来越精确的ATE计算结果,但是这可能会使我们的结果不太可靠,因为假设很强。在具体的应用中,应该要学会权衡如何选择一个看起来还可以,并且可以计算出有意义的结果的假设。具体可参考论文:[Manski (1990), ‘Nonparametric Bounds on Treatment Effects’]
2. Sensitivity Analysis
Sensitivity Basics in Linear Setting

回到本章一开始时的问题,如果充分调整集是 W , U {W, U} W,U,但由于 U U U是观察不到的变量,我们只能对 W W W进行调整,这将会产生多大的误差?

我们以一个线性结构因果模型为例,来探讨这个问题。
假设上面(b)图的结构因果模型如下:
T : = α w W + α u U Y : = β w W + β u U + δ T T:=\alpha_{w} W+\alpha_{u} U\\Y:=\beta_{w} W+\beta_{u} U+\delta T T:=αwW+αuUY:=βwW+βuU+δT
通过 Y Y Y的结构方程可以看出, T T T对 Y Y Y的因果效应为 δ \delta δ,也就是说,
E [ Y ( 1 ) − Y ( 0 ) ] = E W , U [ E [ Y ∣ T = 1 , W , U ] − E [ Y ∣ T = 0 , W , U ] ] = δ \mathbb{E}[Y(1)-Y(0)]=\mathbb{E}_{W, U}[\mathbb{E}[Y \mid T=1, W, U]-\mathbb{E}[Y \mid T=0, W, U]]=\delta E[Y(1)−Y(0)]=EW,U[E[Y∣T=1,W,U]−E[Y∣T=0,W,U]]=δ
通过计算,我们可以得到,
E W [ E [ Y ∣ T = 1 , W , U ] − E [ Y ∣ T = 0 , W , U ] ] = δ + β u α u \mathbb{E}_{W}[\mathbb{E}[Y \mid T=1, W, U]-\mathbb{E}[Y \mid T=0, W, U]]=\delta+\frac{\beta_{u}}{\alpha_{u}} EW[E[Y∣T=1,W,U]−E[Y∣T=0,W,U]]=δ+αuβu
于是,只调整 W W W而忽略 U U U时的误差为 β u α u \frac{\beta_{u}}{\alpha_{u}} αuβu:

下图是误差等高线图,(a)是误差等高线,(b)是ATE计算结果等高线(精确值为25),两图的横坐标代表 1 α u \frac{1}{\alpha_{u}} αu1,纵坐标代表 β u \beta_{u} βu。
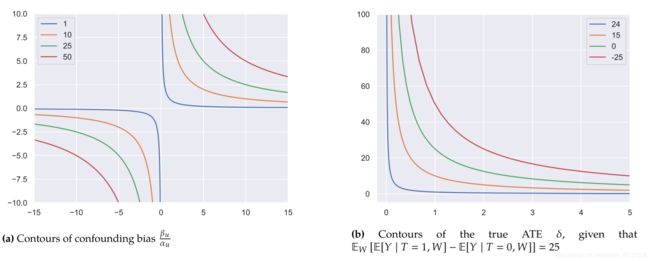
文献中常常使用这种等高线图的方法来进行敏感度分析。
More General Settings
上面的分析中设定了 T T T是 W W W和 U U U的线性函数, Y Y Y是 T T T、 W W W和 U U U的线性函数。而在实际中,结构方程往往是更加复杂的形式。在更加复杂的情况下进行敏感度分析,是目前的一个研究方向,下面只介绍一些工作及其边际价值。



