概率分布介绍：泊松分布

泊松分布 (Poisson Distribution)

定义

假设在一定时间间隔 (interval)中一个事件可能会发生0,1,2,…次，在一个间隔中平均发生事件的次数由$\lambda$决定，$\lambda$是事件发生比率 (event rate)。在一定时间间隔中发生$k$次事件的概率如下：

$P(k\text{ events in interval })=e^{-\lambda }\frac{{\lambda }^k}{k!}$

代码

使用from scipy import stats; stats.poisson.pmf(x,mu)

为什么泊松不得不发明泊松分布?

当时主要的问题是预测未来中发生事件的次数，更正式地说，预测在固定间隔的时间里，预测该事件发生n次的概率。

“事件”可理解为一天中访问你网站的访客数、一天中所接到的电话数。

为什么非得是泊松分布的形式呢？

例如：每周平均有15个人给我的博客点赞，我想预测下一周的点赞数。假设现在并不知道泊松分布，如何解决？可以试试二项分布 ([[Binomial Distribution]])

二项分布

如果使用二项分布来解决，令$x$表示在$n$次重复实验中发生点赞的次数，$p$表示每次实验的点赞概率(Probability)。我们现在已知的是每周平均的点赞比率(rate)为15个赞/周，并不知道点赞概率$p$和博客访客数$n$的任何信息。

因此，我们需要得到更多的信息$p$和$n$，来建模成二项分布问题。

假设过去的1年(=52周)的数据中，一共有10000人看了我的博客，其中有800个人点赞了。这样平均每周访客数=$10000/52=192$，平均每周点赞数=$800/52=15$。可得到概率$p=800/10000=0.08=8\%$

使用二项分布的概率质量函数 (Probability Mass Function)，可预测下一周有20个人点赞的概率为：
$\text{Bin}(m=20\mid N=192,p=0.08)=\frac{N!}{(N-m)!m!}{p}^m(1-p{)}^{N-m}=0.04657$

二项分布的缺点

1. 二项随机变量$x$是只有0或1

上面的过程中，可以将$x$=该周有15次点赞；也可以是$x$=该天有(15/7)=2.1个赞；也可以是$x$=该小时有(15/7*24)=0.1个赞。这意味着大多数小时没有赞，而有的小时有一个点赞。仔细想想，似乎一定时间内出现超过1个点赞的情况也是合理的（比如文章早上刚发布的时候）。由此，二项分布的问题是它无法在一个时间单元中包含超过1次的事件。（在这里，时间单元是1小时）

那么，我们将1小时切分成60分钟，时间单元是1分钟，使得1小时能够包含多个事件。问题得到解决了吗？还没有，比如何同学的5G视频，一晚上点赞就过百万，1分钟内不止一个赞。那我们再将时间单元切分成秒，这样1分钟又能包含多个事件。这样思考下去，我们会将已有的事件单元不断地切分，直到满足一个时间单元只包含一个事件，而大的时间单元能够包含1个以上的事件。

形式化来看，这意味着$n\to \infty$，当我们假定比率(rate)固定，则必须让$p\to 0$。否则，点赞数$n\times p\to \infty$

基于以上的约束，时间单元变得无穷小。我们不用担心同一个时间单元包含一个以上的事件了。

2. 二项分布中，实验次数$n$应该提前知道

在用二项分布时，无法直接用比率(rate)来计算点赞概率$p$，而是需要$n$和$p$才能使用二项分布的概率质量函数。而泊松分布不需要知道$n$和$p$。它假定了$n$是一个无穷大的数，而$p$是无穷小的数。泊松分布的唯一参数是比率$\lambda$（即$x$的期望）。现实中，得知$n$和$p$得进行很多次实验，而短时间内，比率（rate）很容易得到（例如，在下午2点-4点，收到了4个点赞）。

泊松分布的公式推导

泊松分布的特点

1. 泊松分布可看作是对稀有事件的建模，其中的比率$\lambda$可以是任意的，但通常不要太小。

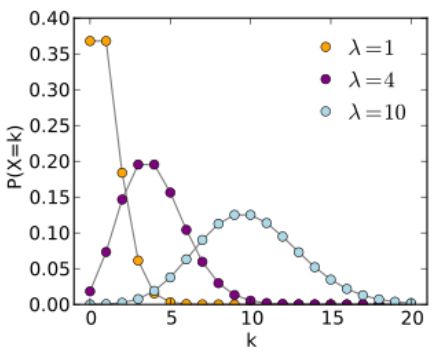
2. 泊松分布是非对称的，通常往右偏移。

3. $\lambda$越大，分布图像越像一个正态分布。图像来自wiki

4. 泊松分布的假设（什么情况适合用泊松分布建模）

每个时间单元的事件平均发生比率是常数

例如：博客的每小时平均点赞数不太可能服从泊松分布，而博客每个月的平均点赞数可近似看作是固定的

事件是独立的

假如你的博客写的很好，被公众号转发推广了，那可能会有大批的读者来阅读，这种情况下的点赞数就不满足泊松分布了。

5. 泊松分布和指数分布的关系

若每个时间单元发生事件的次数服从泊松分布，那么两次事件发生间等待的时间服从指数分布。泊松分布是离散的，而指数分布是连续的，这两个分布紧密相关。

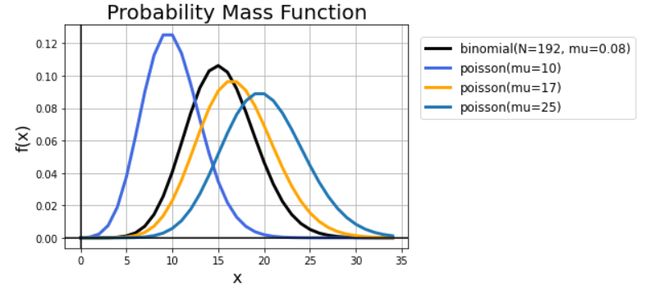
函数图像

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats

# Create x and y
x = np.arange(35)
y1 = stats.binom.pmf(x, 192, 0.08)
y2 = stats.poisson.pmf(x,10)
y3 = stats.poisson.pmf(x,17)
y4 = stats.poisson.pmf(x,20)
# Create the plot
fig, ax = plt.subplots()
plt.plot(x, y1, label='binomial(N=192, mu=0.08)', linewidth=3, color='black')
plt.plot(x, y2, label='poisson(mu=10)', linewidth=3, color='royalblue')
plt.plot(x, y3, label='poisson(mu=17)', linewidth=3, color='orange')
plt.plot(x, y4, label='poisson(mu=25)', linewidth=3)
# Make the x=0, y=0 thicker
# ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')
# Add a title
plt.title('Probability Mass Function', fontsize=20)
# Add X and y Label
plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)', fontsize=16)
# Add a grid
# plt.grid(alpha=.4, linestyle='--')
# Add a Legend
plt.legend(bbox_to_anchor=(1, 1), loc='best', borderaxespad=1, fontsize=12)
# Show the plot
plt.show()

---

参考

Poisson Distribution — Intuition, Examples, and Derivation