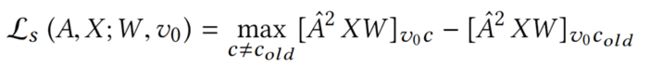基于图神经网络的对抗攻击 Nettack: Adversarial Attacks on Neural Networks for Graph Data
研究意义
随着GNN的应用越来越广，在安全非常重要的应用中应用GNN，存在漏洞可能是非常严重的。
比如说金融系统和风险管理，在信用评分系统中，欺诈者可以伪造与几个高信用客户的联系，以逃避欺诈检测模型；或者垃圾邮件发送者可以轻松地创建虚假的关注者，向社交网络添加错误的信息，以增加推荐和传播重大新闻的机会，或者操控在线评论和产品网站。
因此，我们需要研究对图神经网络的攻击和防御，在我们真正部署一个模型前，应该确认一下这个模型在面对对抗攻击的时候足够健壮？
参考资料
https://zhuanlan.zhihu.com/p/88934914
https://blog.csdn.net/b224618/article/details/82025371
https://blog.csdn.net/travalscx/article/details/84677646
https://www.in.tum.de/en/daml/all-news/news-single-view-en/article/best-paper-award-at-kdd-2018/
- 项目：https://www.in.tum.de/daml/nettack/
- 项目：https://www.in.tum.de/en/daml/research/nettack/
- 代码：https://github.com/danielzuegner/nettack
- poster：https://www.in.tum.de/fileadmin/w00bws/daml/nettack/kdd_poster.pdf
- paper：https://arxiv.org/abs/1805.07984
- talk ppt：https://www.in.tum.de/fileadmin/w00bws/daml/nettack/kdd_talk.pdf
介绍
来自KDD 2018，最佳论文。图神经网络上的对抗攻击的开山之作。
场景
备注：
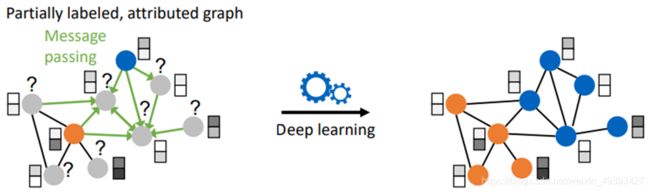
考虑一个简单且经典的场景，图上的结点分类任务。
给定一张图，图上部分结点有标签，通过训练一个深度学习模型来预测图上结点的分类。
一方面预测不基于单独的示例而是联合了图上很多实例的关系效应可能提高鲁棒性；另一方面信息传播带来的级联效应，操纵一个示例可能会影响其他实例，可能会降低鲁棒性。
本文就是研究操纵模型的预测结果是否可能？并且提出一个名叫nettack的对抗攻击算法，来欺骗图深度学习模型。
挑战
- 如何找到有效的制造扰动的算法？
- 如何界定图的扰动不明显、不被注意到？
备注：
想要找到对图神经网络的对抗攻击算法，有两个挑战。
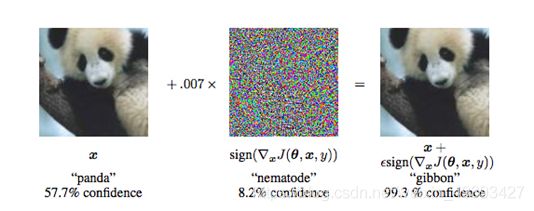
一方面图，不像图像这种由连续特征组成的数据，图的结构和以及大部分情况下的节点特征都是离散的，所以基于梯度构造干扰的方法不适用，那么怎么设计有效的算法来在离散空间找到对抗样本呢？
另一方面对抗样本一个要求是不可分辨性，例如图像，我们可以通过限制每个像素变化很小的值使得人类无法分辨图像的变化。对于大规模的图来说，错综复杂的点和线并不是适合人来观察的，那么怎么定义这种“不可分辨性”呢？
攻击模型
- 投毒攻击（ poisoning attack）
- 发生在模型被训练前，攻击者可以在训练数据中投毒，导致训练的模型出现故障
- 逃逸攻击（ evasion attack）
- 发生在模型被训练以后或者测试阶段，模型已经固定了，攻击者无法对模型的参数或者结构产生影响
备注：
为了解决明确我们的问题，先来讨论一下攻击模型。
图上的结点分类任务一般是直推学习（上节讨论班讲过，简单提一下），就是训练和预测基于同一张图。
可以看图上最上面的例子，这张图一部分是有标签的，在这张图上训练好模型以后，用模型来预测这张图上没有标签的点的标签。
然后逃逸攻击指的是只修改预测时的图，也就是模型参数在训练数据上训练，攻击发生模型被训练以后或者测试阶段，模型已经固定了，攻击者无法对模型的参数或者结构产生影响。
也就是图中的第二个例子。逃逸攻击的应用场景更窄一些。
本文考虑的是投毒攻击，投毒发生在模型被训练前，直接用投毒的数据来训练模型并且在投毒的数据上做预测。
备注：
为了更好的反映现实情况，即攻击者不一定可以直接修改目标结点，可能只能访问除目标结点外的一些结点，或者不能访问整个数据。
因此明确的区分了攻击者结点和目标结点。
- 目标节点：让模型错误分类的结点
- 攻击者结点：攻击者可以操作的结点
同时，又根据攻击者控制的结点不同，可以分为直接攻击和推理攻击：
- 直接攻击：攻击者可以直接操作目标结点，目标结点 == 攻击者结点
- 推理攻击：攻击者只能操作除目标结点以外的结点，目标结点 ∉ 攻击者结点
还有我们可以做出的扰动类型，比如修改结点特征，添加删除边等等。
问题定义
备注：
有了前面的这些知识，我们就可以定义我们的问题。
目标是：在有约束的情况下，最大化目标结点的分类损失，也就是最大化结点在扰动后的图上做预测的标签和真实标签的距离
约束是：第一，扰动是不被注意到的；第二，确保攻击者不能修改整个图，允许的扰动数目是有限制的。第二个约束比较好理解，就是限制做扰动的数目，修改一次结点特征或者添加删除一条边，都算一次扰动。
然后问题是如何定义不被注意到的扰动？
如何定义不被注意的扰动
核心思想：只允许那些保留图的特定固有属性的扰动
备注：
定义不被注意的扰动核心思想是只允许那些保留图特定固有属性的扰动。
对于图结构来说，就是度的分布。因为现实中的图的度分布是符合幂律分布的，所以可以通过检验两张图的度分布是否来自于同一个幂律分布，来判断度的分布有没有明显的改变。
对于结点特征的话，是特征的共现关系。如果一个原图中没有出现的特征在扰动后的图中出现了，这个就是可以被注意到的。方法是：在特征共现图上随机游走，如果有相当大的概率到达一个新加入的特征，那么就认为这个扰动的加入是不被注意的
这里的一些统计量的计算有兴趣或者有需要的可以看一下原文。
这样就定义了如何选择满足条件的扰动，下面考虑如何选择这些满足不被注意条件的扰动，并且应用他们。
替代模型
备注：
为了能够量化扰动的效果，同时简便计算，所以提出了一个替代模型。这个替代模型基于两层的GCN，把激活函数做了线性的替换。
模型有了，对不被注意的扰动的计算也有了，然后考虑如何选择最佳的扰动？
扰动评价
- 替代模型损失
- 找到扰动的图令损失最大
- 评分函数
备注：
我们应该选择让替代模型损失最大化的扰动。
因此引入评分函数，来评价扰动后的替代模型的损失，损失越大说明扰动效果越好。
比如评价结构扰动，因为扰动的是结构，所以特征矩阵不变，计算替代模型的损失函数
算法
备注：
算法是这样的，输入：给定图，目标节点，攻击者结点，改动限制
在原图上训练替代模型去获取参数
在扰动没有达到阈值的的情况下重复循环：
- 找到所有可以不被注意扰动的边
- 选择一个使得S_struct最大的边
- 找到所有可以不被注意扰动的特征
- 选择一个使得S_feat最大的边
- 施加评分高的扰动
跳出循环后输出扰动后的图
其实这个算法得到的扰动后的图并不一定是最好的，因为算法是贪婪的，每一步只考虑局部最优的扰动。
原文中对快速计算扰动候选集合和快速计算得分函数都有详细的推导及证明，感兴趣的可以看一下原文。
下面一起来看一下实验结果
实验结果
备注：
- 这张表中的NETTACK指的是直接攻击
- NEETTACK-IN指的是推理攻击
表中的内容代表结点正确分类的比例，越小说明攻击效果越好
直接攻击的效果要比推理攻击更好
因为这是第一篇嘛，所以对比的baseline是
- FGSM，快速梯度下降法，基于梯度的方法应用于离散数据并不是一个好的选择，实验表明在邻接矩阵中改变元素时，梯度和实际的损失变化不一致
- RND，改变图的结构，随机采样点然后添加边
备注：
这张图描述了在知识受限的情况下，攻击的效果。
知识受限：攻击时候替代模型只在目标节点附近的一定区域内训练。
结果说明了及时知识受限，攻击也是有效的。同时了解的知识越多，需要施加的扰动越少。
图神经网络对抗攻击未来发展方向
- 不可感知的扰动度量：人无法轻易分辨是否有扰动，找到简洁的扰动评估方法很重要
- 研究的图的种类：主要研究集中在带节点属性的静态图，带边属性的图和动态图研究很少
- 图上对抗样本的存在性和可传递性：对于理解图上的学习算法很重要，有助于帮助建立健壮的模型
- 可放缩性：攻击方法的高度复杂性阻碍了在实际中的应用，大多数方法时间复杂度高，基于梯度，降低复杂度仍是一个问题