【竞赛02-b】元胞自动机

0 引入

我们在介绍或者了解一个东西之前，我个人认为比较好的方法就是知道这个东西的具体应用场景如何。在我个人的理解内，元胞自动机像一个模拟器。可以用来模拟一个系统的变化情况。事实上，最初，元胞自动机也是被设计来模拟生物发育中细胞的自我复制。我们可以粗略的认为，元胞自动机是对于一个动态系统的模拟。至于经常使用的方向与系统类型，我将在本文的末尾进行介绍。

1 元胞自动机概念/定义

标准元胞自动机是一个由「元胞、元胞状态、邻域和状态更新规则」构成的四元组，用数学符号可以表示为A=(L,d,S,N,f)

A代表一个元胞自动机系统
L表示元胞空间
d表示元胞自动机内元胞空间的维数，是一正整数
S是元胞有限的、离散的状态集合
N表示某个邻域内所有元胞的集合
f表示局部映射或局部规则。

解释：

• （1）元胞空间：元胞是构成元胞自动机的最基本单元，事实上，笔者在理解上，将元胞一个一个理解为一张棋盘上的棋子，不同的是，也许围棋或者五子棋之类的，落在两根线的交界处，而元胞则在格子中活动。这整张棋盘就是元胞空间。

• （2）元胞状态：元胞只能有一种元胞状态，而且该状态取自一个有限集合。比如{0，1}，{生，死}

• （3）邻域：空间位置上与元胞相邻的细胞称为它的邻元，由所有邻元组成的区域称为它的邻域。领域通常分为一维邻域和二维邻域以及高维邻域。我们可以简单的认为，如果是一维邻域，就是整张棋盘只有一行。而二维就是我们常见的棋盘。

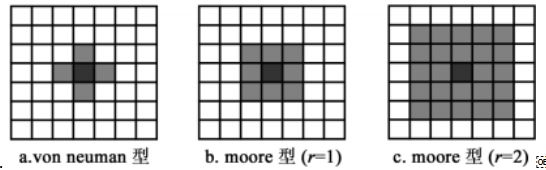
• （4）根据定义的不同，二维邻域常见的邻域类型有：冯·诺依曼(vonNeumanNeighborhoods）、摩尔型(MooreNeighborhoods)、马哥勒斯型(MargolusNeighborhoods)

  
  by the way:一般来说，邻域由r（半径）来决定

• 状态更新规则：
  是指根据元胞当前状态及其邻域中元胞的状态决定下一时刻该元胞状态的状态转移函数
  简而言之，就是一个元胞下一步要自己自己的状态是什么的一个依据。

2 性质

离散性：元胞自动机的空间、时间及状态都是离散的。
同质性：元胞空间中每个单元格可能具有的状态集合相同，并且决定各个元胞状态变化的规则也是相同的。
并行性：元胞空间中各个元胞按状态更新规则变化是同步进行的，特别适合于并行计算，且各个元胞的状态变化是独立行为，互相没有任何影响。
局部性：一个元胞在t+1时刻的状态由其周围半径为r的邻域中的元胞的当前时刻t的状态决定，因此，在时间、空间上都存在着局部性。
维数高：元胞自动机是一类无穷维动力系统。

3 实例-生命游戏

游戏规则说明：在一个二维矩形世界，这个世界中的每个方格居住着一个活着的或死了的细胞。一个细胞在下一个时刻生死取决于相邻八个方格中活着的或死了的细胞的数量。如果相邻方格活着的细胞数量过多，这个细胞会因为资源匮乏而在下一个时刻死去；相反，如果周围活细胞过少，这个细胞会因太孤单而死去。

思考！为何元胞自动机可以模拟它？

答：我们不妨从元胞自动机的几个组成要素来看：

A代表一个元胞自动机系统-------对应生命游戏系统
L表示元胞空间-----------对应这个游戏的二维矩形世界
d表示元胞自动机内元胞空间的维数，是一正整数---二维矩形世界
S是元胞有限的、离散的状态集合----------活着的或死了
N表示某个邻域内所有元胞的集合----------周围的细胞
f表示局部映射或局部规则。-------生死取决于相邻八个方格中活着的或死了的细胞的数量

我们不妨设置取决于周围的细胞的数量为2或者3。试试看这个游戏会如何。
在正式进行这个游戏之前，我们再来熟悉一遍游戏规则：

1. 如果一个细胞周围有3个细胞为生（一个细胞周围共有8个细胞），则该细胞为生（即该细胞若原先为死，则转为生，若原先为生，则保持不变）
2. 如果一个细胞周围有2个细胞为生，则该细胞的生死状态保持不变；
3. 在其它情况下，该细胞为死（即该细胞若原先为生，则转为死，若原先为死，则保持不变）

下面是matlab代码

function ca
m=30;n=30;p=.7;h=100;
for x=1:m
for y=1:n
r=rand(1);
if r>p
a(x,y)=1;
else a(x,y)=0;
end
end
end
for x=1:m
for y=1:n
if a(x,y)==1
fx=[x-1,x-1,x,x];fy=[y-1,y,y,y-1];fill(fx,fy,'g'),hold on
else
end
end
end
for k=1:h
fx=[0,m,m,0];fy=[0,0,n,n];fill(fx,fy,'k'),hold on
for x=2:m-1
for y=2:n-1
b(x,y)=a(x-1,y-1)+a(x-1,y)+a(x-1,y+1)+a(x,y-1)+a(x,y+1)+a(x+1,y-1)+a(x+1,y)+a(x+1,y+1);
if b(x,y)==2,c(x,y)=a(x,y);
elseif b(x,y)==3,c(x,y)=1;
else c(x,y)=0;
end
end
end
c(1:m,1)=a(1:m,1);c(1:m,n)=a(1:m,n);
for x=1:m
for y=1:n
if c(x,y)==1
fx=[x-1,x-1,x,x];fy=[y-1,y,y,y-1];fill(fx,fy,'g'),hold on
else
end
end
end
pause(.05)
a=c;
end

4 应用

引用自维基百科中文站
在社会学中，元胞自动机用于研究政治组织的突现、个人行为的社会性、流言的传播等。
在生物学中，用于肿瘤细胞的增长机理和过程模拟、人类大脑的机理探索、艾滋病病毒HIV的感染过程、自组织、自繁殖等生命现象的研究以及克隆技术的研究。
在计算机科学中，元胞自动机被视为并行计算机而用于并行计算的研究。
在物理学中，除了格子气元胞自动机在流体力学上的成功应用，元胞自动机还应用于磁场、电场等场的模拟，以及热扩散、热传导和机械波的模拟。
在军事科学中，元胞自动机用于模拟军事作战，理解战争过程。
在管理领域，国内外学者开始应用元胞自动机来解释分析各种管理现象，对各种管理现象进行演化模拟。