西瓜书笔记9: 聚类

目录

 

9.1 聚类任务

9.2 性能度量

外部指标

内部指标

9.3 距离计算

有序属性的距离

无序属性的距离

属性距离变形

9.4 原型聚类

k均值算法

学习向量量化(LVQ)

高斯混合聚类

E步

M步

9.5 密度聚类

9.6 层次聚类

---

9.1 聚类任务

无监督学习(unsupervised learning)目标: 揭示数据的内在性质及规律, 为进一步的数据分析提供基础.

聚类(clustering): 将数据集中的样本划分为若干个不相交的子集. (子集=簇(cluster)/类, 由使用者命名)

聚类作用:

1. 找寻数据内在分布结构的单独过程.

2. 分类等其他学习任务的前驱过程.

聚类算法基本问题:

1. 性能度量

2. 距离计算

聚类符号含义

$$ D=\{\boldsymbol x_1,\boldsymbol x_2,\cdots ,\boldsymbol x_m\} $$	样本集D, 包含m个无标记样本
$$ \boldsymbol x_i=(\boldsymbol x_{i1};\boldsymbol x_{i2};\cdots ;\boldsymbol x_{in}) $$	样本xi, n维特征向量
$$ \{C_l|l=1,2,\cdots ,k\} $$	簇C_l 聚类算法将样本集D划分为k个不相交的簇
$$ D=\cup_{l=1}^k C_l $$	划分
$$ C_{l'}\cap_{l'\neq l} C_l=\emptyset $$	不相交
$$ \lambda_j \in \{1,2,\cdots ,k\} $$	簇标记(cluster label)λ_j, 对应样本x_j
$$ \boldsymbol \lambda = (\lambda_1; \lambda_2; \cdots ;\lambda_m) $$	聚类的结果λ 包含m个簇标记元素的向量

9.2 性能度量

聚类中, 有效性指标(validity index)=性能度量

有效性指标作用

1. 评估聚类结果的好坏

2. 作为聚类过程的优化目标

好的聚类结果(目标):

1. 簇内相似度(intra-cluster similarity) 高

2. 簇间相似度(inter-cluster similarity) 低

聚类性能度量/有效性指标类别:

1. 外部指标 (external index): 比较聚类结果与参考模型(reference model)

2. 内部指标 (internal index): 考察聚类结果不利用参考模型

外部指标

利用样本对, 比较聚类结果与参考模型.

符号含义:

	聚类结果	参考模型
簇划分	$$ \mathcal C = \{ C_1; C_2; \cdots ;C_k\} $$	$$ \mathcal C^* = \{ C^*_1; C^*_2; \cdots ;C^*_k\} $$
标记向量	$$ \boldsymbol \lambda $$	$$ \boldsymbol \lambda^* $$

定义变量:

	聚类结果中属于相同簇	聚类结果中属于不同簇
参考模型中属于相同簇	$$ a=|SS|, \\ SS=M_{11}\\=\{ (\boldsymbol x_i,\boldsymbol x_j)|\lambda_i=\lambda_j, \lambda^*_i=\lambda^*_j,i	$$ c=|DS|, \\ DS=M_{01}\\=\{ (\boldsymbol x_i,\boldsymbol x_j)|\lambda_i\neq \lambda_j, \lambda^*_i=\lambda^*_j,i
参考模型中属于不同簇	$$ b=|SD|, \\ SD=M_{10}\\=\{ (\boldsymbol x_i,\boldsymbol x_j)|\lambda_i= \lambda_j,\lambda^*_i\neq \lambda^*_j,i	$$ d=|DD|, \\ DD=M_{00}\\=\{ (\boldsymbol x_i,\boldsymbol x_j)|\lambda_i\neq \lambda_j, \lambda^*_i\neq \lambda^*_j,i

且(xi, xj)组合对的总个数. 根据样本集中有m个样本, xi=1时, 可以取到m-1个xj; xi=2时, 可以取到m-2个xj, 以此类推:

$$ a+b+c+d=\frac{m(m-1)}{2} $$

基于abcd可得聚类性能的外部指标.

以下指标值在[0, 1]内, 值越大越好.

Jaccard系数(Jaccard Coefficient)

$$ \mathrm{JC}=\frac{a}{a+b+c}\\ =\frac{|A\bigcap B|}{|A\bigcup B|}=\frac{|A\bigcap B|}{|A|+|B|-|A\bigcap B|} $$

FM指数(Fowlkes and Mallows Index)

$$ \mathrm{FMI}=\sqrt{\frac{a}{a+b}\cdot \frac{a}{a+c}}\\=\sqrt{\frac{|A\bigcap B|}{A}\cdot \frac{|A\bigcap B|}{B}} $$

其中两个分式为两个非对称指标(概率值往往不一样), 几何平均数将这两个非对称指标转化为一个对称指标.

Rand指数(Rand Index)

$$ \mathrm{RI}=\frac{2(a+d)}{m(m-1)}\\  =\frac{a+d}{a+b+c+d}=\frac{a+d}{m(m-1)/2}\\=\frac{划分正确样本对的数目}{总样本对的数目} $$

内部指标

符号含义(这些距离的大小往往与相似度成反比):

$$ \text{dist}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) $$	两个样本之间的距离
$$ \boldsymbol{\mu}=\frac{1}{|C|} \sum_{1 \leq i \leq|C|} \boldsymbol{x}_{i} $$	簇C的中心点
$$ \text{avg}(C)=\frac{\sum_{1 \leq i	簇C内样本间的平均距离
$$ \text{diam}(C)=\max_{1 \leq i	簇C内样本间的最远距离
$$ \text{d}_{min}(C_i,C_j)=\min_{\boldsymbol{x}_{i} \in C_i, \boldsymbol{x}_{j} \in C_j}\text{dist}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) $$	簇Ci与簇Cj最近样本间的距离
$$ \text{d}_{cen}(C_i,C_j)= \text{dist}\left(\boldsymbol{\mu}_i, \boldsymbol{\mu}_j\right) $$	簇Ci与簇Cj中心点间的距离.
$$ k $$	簇的个数

对于簇划分有以下内部指标:

DB 指数(Davies-Bouldin Index), 值越小越好.

$$ \mathrm{DBI}=\frac{1}{k} \sum_{i=1}^{k} \max _{j \neq i}\left(\frac{\text{avg}\left(C_{i}\right)+\text{avg}\left(C_{j}\right)}{d_{\text{cen}}\left(\boldsymbol{\mu}_{i}, \boldsymbol{\mu}_{j}\right)}\right)\\=\frac{簇内不相似度}{簇间不相似度} $$

Dunn 指数(Dunn Index), 值越大越好.

$$ \mathrm{DI}=\min _{1 \leq i \leq k}\left\{\min _{j \neq i}\left(\frac{d_{\min }\left(C_{i}, C_{j}\right)}{\max _{1 \leq l \leq k} \text{diam}\left(C_{l}\right)}\right)\right\}\\ =\frac{簇间不相似度}{簇内不相似度} $$

9.3 距离计算

距离度量(distance measure)4条基本性质:

非负性	$$ \mathrm{dist}\left(\boldsymbol{x}_{\boldsymbol{i}}, \boldsymbol{x}_{j}\right) \geq 0 $$
同一性	$$ \mathrm{dist}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) \begin{cases}=0, & \boldsymbol{x}_{i}=\boldsymbol{x}_{j}\\ \neq 0, & \boldsymbol{x}_{i}\neq \boldsymbol{x}_{j}\end{cases} $$
对称性	$$ \mathrm{dist}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) =\mathrm{dist}\left(\boldsymbol{x}_{j}, \boldsymbol{x}_{i}\right) $$
直递性	$$ \mathrm{dist}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) \leq \mathrm{dist}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{k}\right)+\mathrm{dist}\left(\boldsymbol{x}_{k}, \boldsymbol{x}_{j}\right) $$

非度量距离(non-metric distance): 不满足距离度量基本性质的相似度度量(similarity measure).

有序属性的距离

有序属性ordinal attribute常用闵可夫斯基距离(Minkowski distance), 即xi, xj的L_p范数.

对于样本的各个属性:

$$ \boldsymbol{x}_{i}=\left(x_{i 1} ; x_{i 2} ; \ldots ; x_{i n}\right) \\ \operatorname{dist}_{m k}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\left(\sum_{u=1}^{n}\left|x_{i u}-x_{j u}\right|^{p}\right)^{\frac{1}{p}} $$

1. p=2时，闵可夫斯基距离=欧氏距离(Euclidean distance)

$$ \operatorname{dist}_{\text {ed }}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right\|_{2}=\sqrt{\sum_{u=1}^{n}\left|x_{i u}-x_{j u}\right|^{2}} $$

2. p=1时，闵可夫斯基距离=曼哈顿距离(Manhattan distance)

$$ \operatorname{dist}_{\operatorname{man}}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right\|_{1}=\sum_{u=1}^{n}\left|x_{i u}-x_{j u}\right| $$

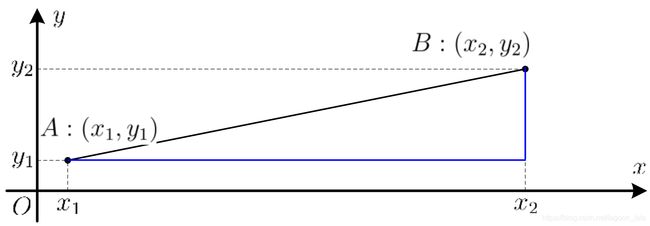
黑线为欧式距离, 蓝线为曼哈顿距离(街区距离city block distance).

无序属性的距离

无序属性non-ordinal attribute可用VDM (Value Difference Metric).

符号含义:

$$ m_{u, a} $$	属性u上取值为a的样本数
$$ m_{u, a, i} $$	第i个样本簇中属性u上取值为a的样本数
$$ k $$	样本簇数

属性u上两个离散值ab之间的 VDM 距离:

$$ \operatorname{VDM}_{p}(a, b)=\sum_{i=1}^{k}\left|\frac{m_{u, a, i}}{m_{u, a}}-\frac{m_{u, b, i}}{m_{u, b}}\right|^{p} $$

属性距离变形

1. 混合属性的距离

即闵可夫斯基距离和VDM结合(其中有序属性n_c个, 无需属性和有序属性共n个):

$$ \operatorname{MinkovDM}_{p}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\left(\sum_{u=1}^{n_{c}}\left|x_{i u}-x_{j u}\right|^{p}+\sum_{u=n_{c}+1}^{n} \operatorname{VDM}_{p}\left(x_{i u}, x_{j u}\right)\right)^{\frac{1}{p}} $$

2. 不同属性权重不同

加权闵可夫斯基距离:

$$ \operatorname{dist}_{\mathrm{wmk}}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\left(w_{1} \cdot\left|x_{i 1}-x_{j 1}\right|^{p}+\ldots+w_{n} \cdot\left|x_{i n}-x_{j n}\right|^{p}\right)^{\frac{1}{p}} $$

9.4 原型聚类

基于原型的聚类(prototype-based clustering).

原型: 是指样本空间中具有代表性的点.

先对原型进行初始化，然后对原型进行迭代更新求解, 常使用EM算法的思想:

两组变量相互影响，但都是未知的.

则初始化其中一组变量，然后计算另一组变量；

再由计算出的变量根据最大似然公式更新前一组变量，反复迭代，直到满足停止条件.

著名的原型聚类算法有: k均值算法, 学习向量量化(LVQ), 高斯混合聚类. 其中k均值算法最常用.

k均值算法

符号含义:

$$ D=\{\boldsymbol x_1,\boldsymbol x_2,\cdots ,\boldsymbol x_m\} $$	样本集D, 包含m个无标记样本
$$ \mathcal C = \{ C_1; C_2; \cdots ;C_k\} $$	簇划分, 共k个簇
$$ \boldsymbol{\mu}_{i}=\frac{1}{\left|C_{i}\right|} \sum_{\boldsymbol{x} \in C_{i}} \boldsymbol{x} $$	簇C_i的中心点 (均值向量)

优化目标为: 簇内样本围绕簇中心点μ的距离=均值误差E. (E值越小则簇内样本相似度越高)

$$ E=\sum_{i=1}^{k} \sum_{\boldsymbol{x} \in C_{i}}\left\|\boldsymbol{x}-\boldsymbol{\mu}_{i}\right\|_{2}^{2} $$

最小化方法: 贪心策略, NP难, 通过迭代优化来近似求解.

算法流程

1. 第1行初始化均值向量;

2. 第 4-8 行(类似E步) 迭代当前簇划分, 第9-16 行(类似M步)迭代更新均值向量;

3. 若迭代更新后聚类结果达到结束条件(如保持不变)，在第 18 行返回当前簇划分结果.

k均值算法:

 西瓜数据集 4.0

number,density,sugercontent 1,0.697,0.460 2,0.774,0.376 3, 0.634,0.264 4,0.608,0.318 5,0.556,0.215 6,0.403,0.237 7,0.481,0.149 7,0.666,0.091 8,0.437,0.211 9,0.666,0.091 10,0.243,0.267 11,0.245,0.057 12,0.343,0.099 13,0.639,0.161 14,0.657,0.198 15,0.360,0.370 16,0.593,0.042 17,0.719,0.103 18,0.359,0.188 19,0.339,0.241 20,0.282,0.257 21,0.748,0.232 22,0.714,0.346 23,0.483,0.312 24,0.478,0.437 25,0.525,0.369 26,0.751,0.489 27,0.532,0.472 28,0.473,0.376 29,0.725,0.445 30,0.446,0.459

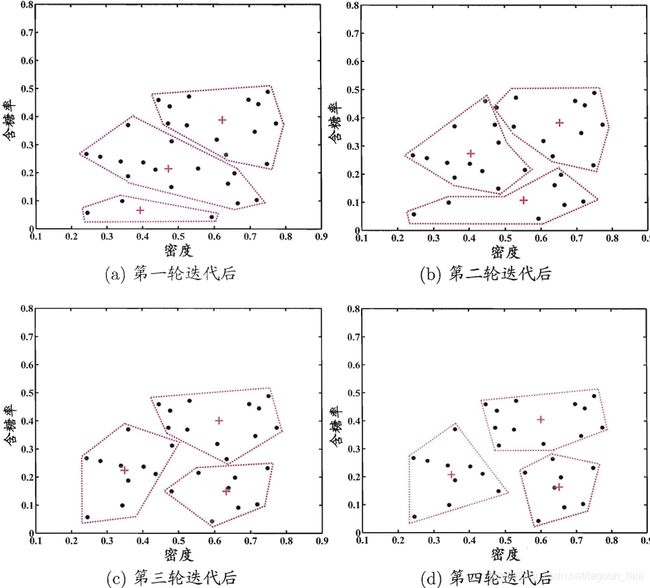
西瓜数据集 4.0的k均值算法(k = 3)在各轮迭代后的结果:

学习向量量化(LVQ)

LVQ学习向量量化(Learning Vector Quantization)特点: 使用有标记样本辅助聚类.

符号含义:

$$ D=\left\{\left(\boldsymbol{x}_{1}, y_{1}\right),\left(\boldsymbol{x}_{2}, y_{2}\right), \ldots,\left(\boldsymbol{x}_{m}, y_{m}\right)\right\} $$	样本集D, 包含m个有标记样本
$$ \boldsymbol{x}_{j}=\left(x_{j 1} ; x_{j 2} ; \ldots ; x_{j n}\right) $$	样本xj的特征向量, 包含n个属性
$$ y_{j} \in \mathcal{Y} $$	样本xj的类别标记
$$ \boldsymbol{p}_{i} \leftrightarrow \\ t_{j} \in \mathcal{Y} $$	原型向量p代表一个簇 簇标记t

学习目标: 一组n维原型向量(原型向量的位置由n个属性值确定)

$$ \left\{\boldsymbol{p}_{1}, \boldsymbol{p}_{2}, \ldots, \boldsymbol{p}_{q}\right\} $$

LVQ 算法流程:

1. 先初始化原型向量. 从类别标记为t_q的样本中随机选取一个作为原型向量.

2. 原型向量迭代优化. 随机选取一个有标记训练样本，找出与其距离最近的原型向量，井根据两者的类别标记是否一致更新原型向量. (竞争学习策略)

3. 若算法满足停止条件，将当前原型向量作为最终结果返回.

LVQ算法描述:

其中, 最近的原型向量与样本类别标记相同时, 更新后原型向量与样本距离减小, 更接近:

$$ \begin{aligned} \left\|\boldsymbol{p}^{\prime}-\boldsymbol{x}_{j}\right\|_{2} &=\left\|\boldsymbol{p}_{i^{*}}+\eta \cdot\left(\boldsymbol{x}_{j}-\boldsymbol{p}_{i^{*}}\right)-\boldsymbol{x}_{j}\right\|_{2} \\ &=(1-\eta) \cdot\left\|\boldsymbol{p}_{i^{*}}-\boldsymbol{x}_{j}\right\|_{2}, \end{aligned}\\ \eta\in (0,1) $$

类似地类别标记不同时, 距离增大:

$$ \left\|\boldsymbol{p}^{\prime}-\boldsymbol{x}_{j}\right\|_{2}= (1+\eta) \cdot\left\|\boldsymbol{p}_{i^{*}}-\boldsymbol{x}_{j}\right\|_{2} $$

根据所得的一组原型向量, 可对样本空间进行Voronoi剖分(Voronoi tessellation):

每个原型向量p定义了与之相关的一个区域R，该区域中每个样本与pi的距离比其他原型近:

$$ R_{i}=\left\{\boldsymbol{x} \in \mathcal{X} \mid\left\|\boldsymbol{x}-\boldsymbol{p}_{i}\right\|_{2} \leq\left\|\boldsymbol{x}-\boldsymbol{p}_{i^{\prime}}\right\|_{2}, i^{\prime} \neq i\right\} $$

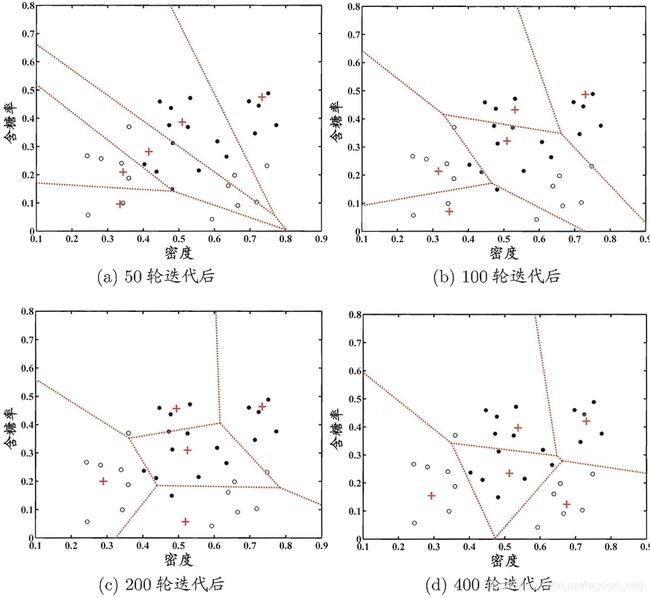
西瓜数据集4.0上 LVQ算法(q=5)的聚类结果(Voronoi剖分):

高斯混合聚类

高斯混合(Mixture-of-Gaussian)聚类: 用概率模型表达聚类原型.

(多元)高斯分布概率密度函数:

$$ p(\boldsymbol{x})=p(\boldsymbol{x}|\boldsymbol{\mu},\mathbf{\Sigma})=\\ \frac{1}{(2 \pi)^{\frac{n}{2}}|\mathbf{\Sigma}|^{\frac{1}{2}}} e^{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})} $$

其中, 高斯分布完全由均值向量μ, 协方差矩阵Σ两个参数确定.

高斯混合分布(k个高斯加权求和)

$$ p_{\mathcal{M}}(\boldsymbol{x})=\sum_{i=1}^{k} \alpha_{i} \cdot p\left(\boldsymbol{x} \mid \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right) $$

符号含义:

$$ k $$	混合分布中高斯分布个数
$$ \boldsymbol{\mu}_i,\mathbf{\Sigma}_i $$	第i个高斯混合成分参数
$$ \alpha_{i}>0, \sum_{i=1}^{k} \alpha_{i} =1 $$	混合系数mixture coefficient, 样本属于第i个混合成分的概率, 第i个高斯混合成分被选到的概率为αi

样本生成过程:

1. 根据先验分布α, 从k个高斯中选择一个高斯混合成分. 假设选到了第i个高斯混合成分，其参数为μi, Σi.

2. 根据概率密度函数p(x|μi, Σi), 从x定义域采样生成样本x.

高斯混合聚类算法描述

1. 第1行初始化高斯混合分布的模型参数.

2. 第2-12 行基于 EM 算法迭代更新模型参数, 直到停止条件满足.

3. 第14-17 行根据高斯混合分布确定簇划分.

获取高斯混合模型参数使用EM算法

在每步迭代中:

1. (E步)根据当前参数计算每个样本属于每个高斯成分的后验概率γ.

2. (M步)根据α, μ, Σ求解公式更新模型参数.

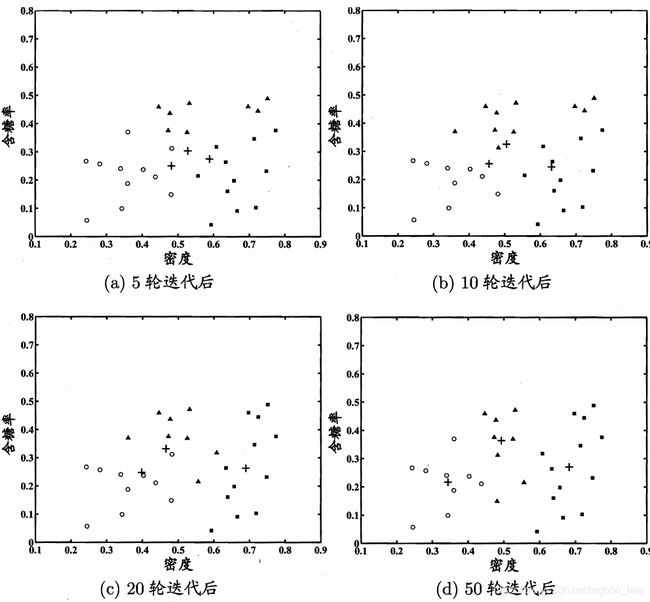
高斯混合聚类(k=3)的聚类结果-其中样本簇1, 2, 3,样本点分别用 "⚪" "■"与"▲"表示，高斯混合成分的均值向量用"+"表示:

E步

高斯混合聚类采用概率模型(高斯分布)刻画原型，簇划分由原型对应后验概率确定..

符号含义:

$$ D=\{\boldsymbol x_1,\boldsymbol x_2,\cdots ,\boldsymbol x_m\} $$	训练集D
$$  z_j \in \{1,2,\cdots ,k\}  $$	生成样本x_j的高斯混合成分z_j
$$ p_{\mathcal{M}}\left(z_{j}=i \mid \boldsymbol{x}_{j}\right)= γ_{ji} $$	样本x_j由第i个高斯混合成分z_i生成的后验概率γ_ji, 可用来进行簇划分
$$ P\left(z_{j}=i\right)= \alpha_{i} $$	第i个高斯混合成分z_i生成样本x_j的先验概率α_i, 可用来选择高斯成分, i
$$ p_{\mathcal{M}}\left(\boldsymbol{x}_{j}\right)\\ =\sum_{l=1}^{k} \alpha_{l} \cdot p \left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right) $$	生成样本x_j使用的高斯混合分布p_M

其中, γ_ji(样本x_j由第i个高斯混合成分z_i生成的后验概率)根据后验概率的贝叶斯公式, 代入先验概率与高斯混合分布:

$$ \begin{aligned} γ_{ji}&=p_{\mathcal{M}}\left(z_{j}=i \mid \boldsymbol{x}_{j}\right) \\ &=\frac{P\left(z_{j}=i\right) \cdot p_{\mathcal{M}}\left(\boldsymbol{x}_{j} \mid z_{j}=i\right)}{p_{\mathcal{M}}\left(\boldsymbol{x}_{j}\right)} \\ &=\frac{\alpha_{i} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)} \end{aligned} $$

计算可得γ组成的矩阵Γ:

$$ \Gamma=\left[\begin{array}{cccc} \gamma_{11} & \gamma_{12} & \cdots & \gamma_{1 k} \\ \gamma_{21} & \gamma_{22} & \cdots & \gamma_{2 k} \\ \vdots & \vdots & \ddots & \vdots \\ \gamma_{m 1} & \gamma_{m 2} & \cdots & \gamma_{m k} \end{array}\right]_{m \times k}  $$

其中γji为第j行第i列的元素，矩阵大小为训练集样本个数m *高斯混合模型成分个数k.

假设高斯混合分布己知, 利用后验概率γ可进行簇划分, 得到簇标记λ为矩阵Γ第j行的所有k 个元素中最大的那个元素的位置:

$$ \lambda_{j}=\underset{i \in\{1,2, \ldots, k\}}{\arg \max } \gamma_{j i} $$

M步

已知样本集D, 簇划分λ, 求模型参数的方法: 最大化对数似然(对数防止连乘下溢)

对数似然公式(m个样本一起出现的概率):

$$ \begin{aligned} L L(D) &=\ln \left(\prod_{j=1}^{m} p_{\mathcal{M}}\left(\boldsymbol{x}_{j}\right)\right) \\ &=\sum_{j=1}^{m} \ln \left(\sum_{i=1}^{k} \alpha_{i} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)\right) \end{aligned} $$

因此, 目标为: 求参数Σ, μ, α, 最大化LL(D).

求μ

样本加权平均, 估计各混合成分的均值μ. (其中样本权重γ是每个样本属于该成分的后验概率):

$$ \boldsymbol\mu_{i}=\frac{\sum_{j=1}^{m} \gamma_{j i} \boldsymbol{x}_{j}}{\sum_{j=1}^{m} \gamma_{j i}} $$

推导过程:

求最大化LL(D)的μ, 即求:

$$ \frac{\partial L L(D)}{\partial \boldsymbol{\mu}_{i}}=0\\ =\frac{\partial L L(D)}{\partial p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)} \cdot \frac{\partial p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)}{\partial \boldsymbol{\mu}_{i}} $$

其中, 代入:

$$ p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)=\frac{1}{(2 \pi)^{\frac{n}{2}}\left|\boldsymbol{\Sigma}_{i}\right|^{\frac{1}{2}}} \exp \left(-\frac{1}{2}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)^{T} \boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)\right) $$

$$ LL(D)=\sum_{j=1}^{m} \ln \left(\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)\right) $$

1. 得其中第一项

$$ \begin{aligned} \frac{\partial L L(D)}{\partial p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \mathbf{\Sigma}_{i}\right)} &=\frac{\partial \sum_{j=1}^{m} \ln \left(\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)\right)}{\partial p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)} \\ &=\sum_{j=1}^{m} \frac{\partial \ln \left(\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)\right)}{\partial p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)} \\ &=\sum_{j=1}^{m} \frac{\alpha_{i}}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)} \end{aligned} $$

2. 得其中第二项

$$ \begin{aligned} &\frac{\partial p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)}{\partial \boldsymbol{\mu}_{i}}\\ &=\frac{\partial \frac{1}{(2 \pi)^{\frac{n}{2}}\left|\Sigma_{i}\right|^{\frac{1}{2}}} \exp\left({-\frac{1}{2}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)^{\top}\boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)}\right)}{\partial \boldsymbol{\mu}_{i}} \\ &=\frac{1}{(2 \pi)^{\frac{n}{2}}\left|\boldsymbol{\Sigma}_{i}\right|^{\frac{1}{2}}} \cdot \frac{\partial \exp\left({-\frac{1}{2}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)^{\top} \boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)}\right)}{\partial \boldsymbol{\mu}_{i}}\\ \\ &=\frac{1}{(2 \pi)^{\frac{n}{2}}\left|\boldsymbol{\Sigma}_{i}\right|^{\frac{1}{2}}}\cdot \exp\left({-\frac{1}{2}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)^{\top} \boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)}\right) \cdot-\frac{1}{2} \frac{\partial\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)^{\top} \boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)}{\partial \boldsymbol{\mu}_{i}} \end{aligned} $$

此处代入矩阵求导的法则:

$$ \frac{\partial \mathbf{a}^{T} \mathbf{X} \mathbf{a}}{\partial \mathbf{a}}=2\mathbf{X} \mathbf{a}  $$

$$ \begin{aligned} &-\frac{1}{2} \frac{\partial\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)^{\top} \boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)}{\partial \boldsymbol{\mu}_{i}} \\ &=-\frac{1}{2} \cdot 2 \boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{\mu}_{i}-\boldsymbol{x}_{j}\right) \\ &=\boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right) \end{aligned} $$

得:

$$ \begin{aligned} &\frac{\partial p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)}{\partial \boldsymbol{\mu}_{i}}\\ \\ &=\frac{1}{(2 \pi)^{\frac{n}{2}}\left|\boldsymbol{\Sigma}_{i}\right|^{\frac{1}{2}}}\cdot \exp\left({-\frac{1}{2}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)^{\top} \boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)}\right) \cdot\boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)\\ &=p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right) \cdot \boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right) \end{aligned} $$

3. 两项结合, 有:

$$ \frac{\partial L L(D)}{\partial \boldsymbol{\mu}_{i}}=0\\ =\sum_{j=1}^{m} \frac{\alpha_{i}}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{l}, \mathbf{\Sigma}_{l}\right)} \cdot p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right) \cdot \boldsymbol{\Sigma}_{i}^{-1}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right)\\ =\sum_{j=1}^{m} \frac{\alpha_{i} \cdot p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} | \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right) $$

其中, 因为对j求和时Σ_i为常数, 对μ最大化时可消掉因式Σ_i^{-1}, 而α留着凑γ.

代入γ:

$$ \begin{aligned} γ_{ji}&=p_{\mathcal{M}}\left(z_{j}=i \mid \boldsymbol{x}_{j}\right) \\ &=\frac{\alpha_{i} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)} \end{aligned} $$

可得:

$$ \frac{\partial L L(D)}{\partial \boldsymbol{\mu}_{i}}=0\\ =\sum_{j=1}^{m} \gamma_{j i}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}\right) $$

移项解出μ:

$$ \boldsymbol\mu_{i}=\frac{\sum_{j=1}^{m} \gamma_{j i} \boldsymbol{x}_{j}}{\sum_{j=1}^{m} \gamma_{j i}} $$

求Σ

$$ \mathbf\Sigma_{i}=\frac{\sum_{j=1}^m\gamma_{ji}(\boldsymbol x_{j}-\boldsymbol \mu_{i})(\boldsymbol x_{j}-\boldsymbol\mu_{i})^T}{\sum_{j=1}^m\gamma_{ji}} $$

推导过程:

代入LL(D), 对Σ求导, 根据ln的复合函数链式求导:

$$ \begin{aligned} \cfrac {\partial LL(D)}{\partial\mathbf\Sigma_{i}}&=0\\ &=\cfrac {\partial}{\partial \mathbf\Sigma_{i}}\left[\sum_{j=1}^m\ln\Bigg(\sum_{i=1}^k \alpha_{i}\cdot p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})\Bigg)\right] \\ &=\sum_{j=1}^m\frac{\partial}{\partial\mathbf\Sigma_{i}}\left[\ln\Bigg(\sum_{i=1}^k \alpha_{i}\cdot p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})\Bigg)\right] \\ &=\sum_{j=1}^m\cfrac{\alpha_{i}}{\sum_{l=1}^k\alpha_{l}\cdot p(\boldsymbol x_{j}|\boldsymbol\mu_{l},\mathbf\Sigma_{l})} \cdot \cfrac{\partial p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})}{\partial\mathbf\Sigma_{i}} \end{aligned} $$

其中, 后一项因式代入高斯分布概率密度函数, 得:

$$ \begin{aligned} &\cfrac{\partial}{\partial\mathbf\Sigma_{i}}\left(p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})\right)\\ &=\cfrac{\partial}{\partial\mathbf\Sigma_{i}}\left[\cfrac{1}{(2\pi)^\frac{n}{2}\left| \mathbf\Sigma_{i}\right |^\frac{1}{2}}\exp\left({-\frac{1}{2}(\boldsymbol x_{j}-\boldsymbol\mu_{i})^T\mathbf\Sigma_{i}^{-1}(\boldsymbol x_{j}-\boldsymbol\mu_{i})}\right)\right] \end{aligned} $$

1. 此处利用e^ln配凑, 化乘除为加减(否则直接除法求导公式会比较冗长):

$$ p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})=e^{\ln(p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i}))}\\ \Rightarrow \cfrac{\partial}{\partial\mathbf\Sigma_{i}}e^{\ln(p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i}))}\\ =e^{\ln(p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i}))}\cdot \cfrac{\partial \ln(p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i}))}{\partial\mathbf\Sigma_{i}} $$

则该项可化为:

$$ \begin{aligned} &\cfrac{\partial}{\partial\mathbf\Sigma_{i}}\left(p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})\right)\\ &=\cfrac{\partial}{\partial\mathbf\Sigma_{i}}\left\{\exp\left[\ln\left(\cfrac{1}{(2\pi)^\frac{n}{2}\left| \mathbf\Sigma_{i}\right |^\frac{1}{2}}\exp\left({-\frac{1}{2}(\boldsymbol x_{j}-\boldsymbol\mu_{i})^T\mathbf\Sigma_{i}^{-1}(\boldsymbol x_{j}-\boldsymbol\mu_{i})}\right)\right)\right]\right\} \\ &=p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})\cdot\cfrac{\partial}{\partial\mathbf\Sigma_{i}}\left[\ln\left(\cfrac{1}{(2\pi)^\frac{n}{2}\left| \mathbf\Sigma_{i}\right |^\frac{1}{2}}\exp\left({-\frac{1}{2}(\boldsymbol x_{j}-\boldsymbol\mu_{i})^T\mathbf\Sigma_{i}^{-1}(\boldsymbol x_{j}-\boldsymbol\mu_{i})}\right)\right)\right]\\ &=p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})\cdot\cfrac{\partial}{\partial\mathbf\Sigma_{i}}\left[\ln\cfrac{1}{(2\pi)^{\frac{n}{2}}}-\cfrac{1}{2}\ln{|\mathbf{\Sigma}_i|}-\frac{1}{2}(\boldsymbol x_j-\boldsymbol\mu_i)^T\mathbf{\Sigma}_i^{-1}(\boldsymbol x_j-\boldsymbol\mu_i)\right]\\ &=p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})\cdot\left[-\cfrac{1}{2}\cfrac{\partial\left(\ln{|\mathbf{\Sigma}_i|}\right) }{\partial \mathbf{\Sigma}_i}-\cfrac{1}{2}\cfrac{\partial \left[(\boldsymbol x_j-\boldsymbol\mu_i)^T\mathbf{\Sigma}_i^{-1}(\boldsymbol x_j-\boldsymbol\mu_i)\right]}{\partial \mathbf{\Sigma}_i}\right]\\ \end{aligned} $$

2. 此处利用矩阵微分公式, 与正定矩阵Σ的对称性(矩微分公式参考《The Matrix Cookbook》2.4节矩阵, 向量, 和标量的导数):

$$ \cfrac{\partial |\mathbf{X}|}{\partial \mathbf{X}}=|\mathbf{X}|\cdot(\mathbf{X}^{-1})^{T},\\ \cfrac{\partial \boldsymbol{a}^{T} \mathbf{X}^{-1} \boldsymbol{b}}{\partial \mathbf{X}}=-\mathbf{X}^{-T} \boldsymbol{a b}^{T} \mathbf{X}^{-T}  $$

$$ \frac{\partial\left(\ln{|\mathbf{\Sigma}_i|}\right) }{\partial \mathbf{\Sigma}_i}=\frac{1}{|\mathbf{\Sigma}_i|}\cdot |\mathbf{\Sigma}_i|(\mathbf{\Sigma}_i^{-1})^T\\ =\mathbf{\Sigma}_i^{-1} $$

得该项为:

$$ \begin{aligned} \cfrac{\partial}{\partial\mathbf\Sigma_{i}}\left(p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})\right)&=p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})\cdot\left[-\cfrac{1}{2}\mathbf{\Sigma}_i^{-1}+\cfrac{1}{2}\mathbf{\Sigma}_i^{-1}(\boldsymbol x_j-\boldsymbol\mu_i)(\boldsymbol x_j-\boldsymbol\mu_i)^T\mathbf{\Sigma}_i^{-1}\right]\\ \end{aligned} $$

该部分带回原式为:

$$ \frac {\partial LL(D)}{\partial\mathbf\Sigma_{i}}=\sum_{j=1}^m\cfrac{\alpha_{i}\cdot p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})}{\sum_{l=1}^k\alpha_{l}\cdot p(\boldsymbol x_{j}|\boldsymbol\mu_{l},\mathbf\Sigma_{l})}\cdot\left[-\frac{1}{2}\mathbf{\Sigma}_i^{-1}+\frac{1}{2}\mathbf{\Sigma}_i^{-1}(\boldsymbol x_j-\boldsymbol\mu_i)(\boldsymbol x_j-\boldsymbol\mu_i)^T\mathbf{\Sigma}_i^{-1}\right] $$

代入γ:

$$ \gamma_{ji} =\frac{\alpha_{i}\cdot p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})}{\sum_{l=1}^k\alpha_{l}\cdot p(\boldsymbol x_{j}|\boldsymbol\mu_{l},\mathbf\Sigma_{l})} $$

原式可化为:

$$ \begin{aligned} 0&=\cfrac {\partial LL(D)}{\partial\mathbf\Sigma_{i}}\\&=\sum_{j=1}^m\gamma_{ji}\cdot\left[-\cfrac{1}{2}\mathbf{\Sigma}_i^{-1}+\cfrac{1}{2}\mathbf{\Sigma}_i^{-1}(\boldsymbol x_j-\boldsymbol\mu_i)(\boldsymbol x_j-\boldsymbol\mu_i)^T\mathbf{\Sigma}_i^{-1}\right]\\ &=\sum_{j=1}^m\gamma_{ji}\cdot\left[-\boldsymbol{I}+(\boldsymbol x_j-\boldsymbol\mu_i)(\boldsymbol x_j-\boldsymbol\mu_i)^T\mathbf{\Sigma}_i^{-1}\right]  \end{aligned} $$

移项可解出Σ:

$$ \begin{aligned} \\ \sum_{j=1}^m\gamma_{ji}(\boldsymbol x_j-\boldsymbol\mu_i)(\boldsymbol x_j-\boldsymbol\mu_i)^T\mathbf{\Sigma}_i^{-1}&=\sum_{j=1}^m\gamma_{ji}\boldsymbol{I}\\ \sum_{j=1}^m\gamma_{ji}(\boldsymbol x_j-\boldsymbol\mu_i)(\boldsymbol x_j-\boldsymbol\mu_i)^T&=\sum_{j=1}^m\gamma_{ji}\mathbf{\Sigma}_i\\ \mathbf{\Sigma}_i^{-1}\cdot\sum_{j=1}^m\gamma_{ji}(\boldsymbol x_j-\boldsymbol\mu_i)(\boldsymbol x_j-\boldsymbol\mu_i)^T&=\sum_{j=1}^m\gamma_{ji}\\ \mathbf{\Sigma}_i&=\cfrac{\sum_{j=1}^m\gamma_{ji}(\boldsymbol x_j-\boldsymbol\mu_i)(\boldsymbol x_j-\boldsymbol\mu_i)^T}{\sum_{j=1}^m\gamma_{ji}} \end{aligned} $$

求α

每个高斯成分的混合系数αi, 由样本属于该成分的后验概率γji平均值确定:

$$ \alpha_{i}=\frac{1}{m}\sum_{j=1}^m\gamma_{ji} $$

推导过程:

求混合系数α，为有条件极值问题. 最大化LL(D) 时, 还需满足条件:

$$ \alpha_{i} \geq 0, \sum_{i=1}^{k} \alpha_{i}=1 $$

使用拉格朗日乘子法(其中λ为乘子):

$$ L L(D)+\lambda\left(\sum_{i=1}^{k} \alpha_{i}-1\right) $$

代入LL(D), 第一项第二项分别对αi求导:

$$ \begin{aligned} \frac{\partial L L(D)}{\partial \alpha_{i}} &=\frac{\partial \sum_{j=1}^{m} \ln \left(\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)\right)}{\partial \alpha_{i}} \\ &=\sum_{j=1}^{m} \frac{1}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)} \cdot \frac{\partial \sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)}{\partial \alpha_{i}} \\ &=\sum_{j=1}^{m} \frac{1}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right) \\ \lambda \frac{\partial\left(\sum_{l=1}^{k} \alpha_{l}-1\right)}{\partial \alpha_{i}} &=\lambda \frac{\partial\left(\alpha_{1}+\alpha_{2}+\ldots+\alpha_{i}+\ldots+\alpha_{k}-1\right)}{\partial \alpha_{i}}\\ &=\lambda \cdot 1 \end{aligned} $$

Σαl对αi求导时, 注意展开, 只有l=i的一项保留下来.

两项结合, 得到:

$$ \sum_{j=1}^{m} \frac{p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)} +\lambda=0 $$

两边同乘αi可凑后验概率γji:

$$ \sum_{j=1}^m\frac{\alpha_{i}\cdot p(\boldsymbol x_{j}|\boldsymbol\mu_{i},\mathbf\Sigma_{i})}{\sum_{l=1}^k\alpha_{l}\cdot p(\boldsymbol x_{j}|\boldsymbol\mu_{l},\mathbf\Sigma_{l})}+\lambda\alpha_{i}=0\\ \Rightarrow \sum_{j=1}^{m} \gamma_{j i}+\lambda \alpha_{i}=0 $$

利用α作为权重的性质:

$$ \sum_{i-1}^{k} \alpha_{i}=1 $$

$$ \sum_{i-1}^{k} \lambda \alpha_{i}=\lambda \sum_{i-1}^{k} \alpha_{i}=\lambda\\ \begin{aligned} \sum_{i=1}^{k} \gamma_{j i} &=\sum_{i=1}^{k} \frac{\alpha_{i} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)} \\ &=\frac{\sum_{i=1}^{k} \alpha_{i} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right)}{\sum_{l=1}^{k} \alpha_{l} \cdot p\left(\boldsymbol{x}_{j} \mid \boldsymbol{\mu}_{l}, \boldsymbol{\Sigma}_{l}\right)} \end{aligned} $$

对所有k个混合成分求和:

$$ 0=\sum_{i=1}^{k} \sum_{j=1}^{m} \gamma_{j i}+ \lambda\\ =\sum_{j=1}^{m} \sum_{i=1}^{k} \gamma_{j i}+ \lambda\\ =\sum_{j=1}^{m} 1+ \lambda\\ =m+ \lambda $$

得λ=-m, 将λ代入原式(不对所有混合成分求和):

$$ \sum_{j=1}^{m} \gamma_{j i}+\lambda \alpha_{i}=0\\ \Rightarrow \sum_{j=1}^{m} \gamma_{j i}=-\lambda \alpha_{i}=m\alpha_{i}\\ \Rightarrow \alpha_{i}=\frac{1}{m}\sum_{j=1}^m\gamma_{ji} $$

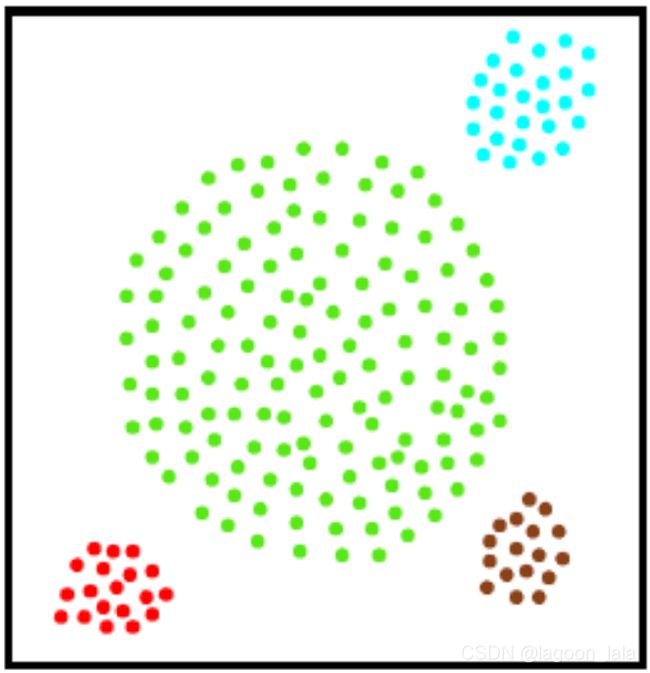
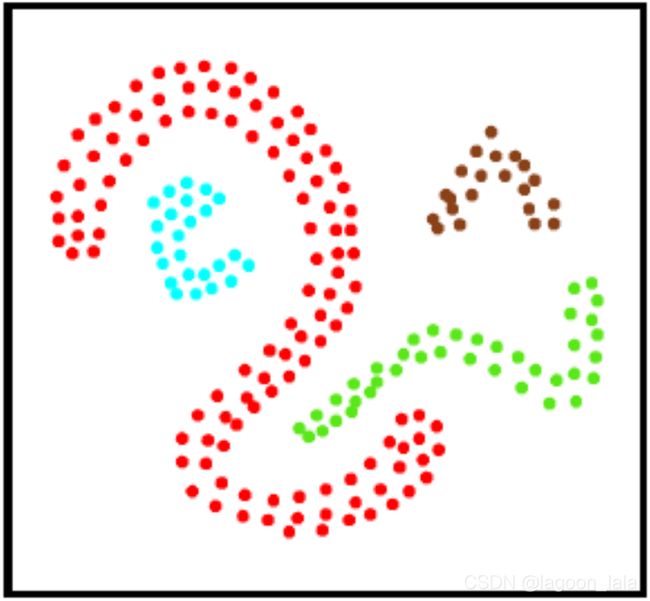
9.5 密度聚类

基于密度的聚类(density-based clustering): 从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇, 获得聚类结果.

密度聚类与原型聚类的区别:

	均值算法	DBSCAN
聚类使用的距离度量	欧氏距离	类似于测地线距离
产生聚类的类型	凸聚类	非凸聚类

密度聚类优点:

1. 可以产生任意形状的簇

2. 不需要事先指定聚类个数k

3. 对噪声鲁棒

以下介绍经典密度聚类算法DBSCAN(Density-Based Spatial Clustering of Applications with Noise).

变量含义:

$$ D=\{\boldsymbol x_1,\boldsymbol x_2,\cdots ,\boldsymbol x_m\} $$	样本集D, 包含m个无标记样本
$$ \operatorname{dist}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right\|_{2}=\sqrt{\sum_{u=1}^{n}\left|x_{i u}-x_{j u}\right|^{2}} $$	欧氏距离

常用概念:

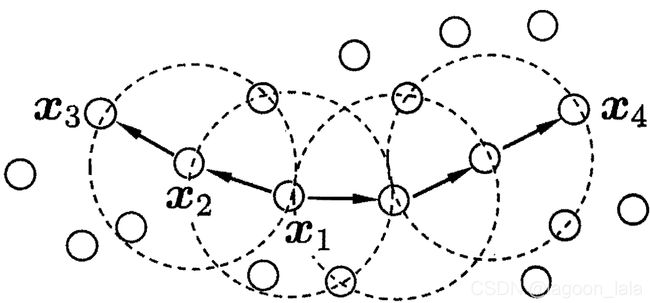
ϵ-邻域 (图中虚线圈)	与x_j距离不大于ϵ $$ N_{\epsilon}\left(\boldsymbol{x}_{j}\right)= \left\{\boldsymbol{x}_{i} \in D \mid \operatorname{dist}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) \leq \epsilon\right\} $$
核心对象(core object) (MinPts = 3, 图中x1)	邻域内至少包含 MinPts 个样本的对象 $$ |N_{\epsilon}\left(\boldsymbol{x}_{j}\right)|\geq MinPst $$
密度直达(directly density reachable) x2由x1密度直达 x1->x2	1. x_i核心 2. x_j在x_i领域 不满足对称性
密度可达(density-reachable) (x3由x1密度可达) x1->…->x3	样本序列p_1, p_2, … , p_n p_{i+1}由p_i传递密度直达, 即最后只有p_n不是核心对象. 不满足对称性
密度相连(density-connected) (x3与x4密度可达) x3<-xk->x4	由一个中间样本对两样本均密度可达. (两个相连样本不需要是核心对象, 但中间样本是核心对象) 满足对称性

簇定义: 最大的密度相连样本集合.

噪声(noise)/异常(anomaly)样本: D中不属于任何簇的样本

簇性质

1. 连接性(connectivity): 簇内任意两样本密度相连.

2. 最大性(maximality): 可达样本均在同簇.

找簇思想:

1. 找到核心对象x

2. 由x密度可达的所有样本组成的集合为满足连接性与最大性的簇:

$$ X=\left\{\boldsymbol{x}^{\prime} \in D \mid\right.\boldsymbol{x}^{\prime}由\boldsymbol{x}密度可达\} $$

DBSCAN算法流程:

1. 根据给定的邻域参数(ϵ, MinPts)找出所有核心对象.

2. 以任一核心对象为出发点，找出由其密度可达的样本生成聚类簇, 直到所有核心对象均被访问过.

DBSCA算法(ϵ = 0.11, MinPts=5) 生成聚类簇, 其中核心对象, 非核心对象, 噪声样本分别用'●', '⚪', '*'表示:

9.6 层次聚类

层次聚类(hierarchical clustering): 在不同层次划分数据集，形成树形聚类结构.

层次聚类数据集的划分:

1. 聚合策略: 自底向上, 算法AGNES(AGglomerative NESting)

2, 分拆策略: 自顶向下, 算法DIANA

簇间距计算(常用豪斯多夫距离Hausdorff distance):

簇间最小距离(单链接)	$$ d_{\min }\left(C_{i}, C_{j}\right)=\min _{x \in C_{i}, \boldsymbol{z} \in C_{j}} \mathrm{dist}(\boldsymbol{x}, \boldsymbol{z}) $$
簇间最大距离(全链接)	$$ d_{\max }\left(C_{i}, C_{j}\right)=\max _{\boldsymbol{x} \in C_{i}, \boldsymbol{z} \in C_{j}} \mathrm{dist}(\boldsymbol{x}, \boldsymbol{z}) $$
簇间平均距离(均链接)	$$ d_{\mathrm{avg}}\left(C_{i}, C_{j}\right)=\frac{1}{\left|C_{i}\right|\left|C_{j}\right|} \sum_{\boldsymbol{x} \in C_{i}} \sum_{\boldsymbol{z} \in C_{j}} \mathrm {dist}(\boldsymbol{x}, \boldsymbol{z}) $$
距离矩阵M	第i行: 聚类簇C_i到各聚类簇的距离 第i列: 各聚类簇到聚类簇C_i的距离

对比两点间距, 簇内距:

两个样本之间的距离	$$ \text{dist}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) $$
簇C内样本间的平均距离	$$ \text{avg}(C)=\frac{\sum_{1 \leq i
簇C内样本间的最远距离	$$ \text{diam}(C)=\max_{1 \leq i

AGNES算法描述:

1. 先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化

2. 并距离最近的聚类簇，井对合并得到的聚类簇的距离矩阵进行更新, 直至达到预设的聚类簇数.

其中簇C_j合并到簇C_i时需要:

删除距离矩阵M的第j行与第j列,

更新距离矩阵M的第i行与第i列.

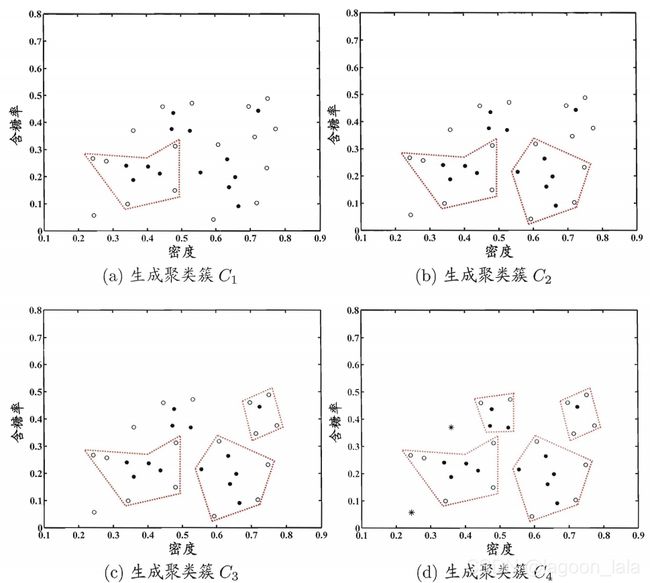
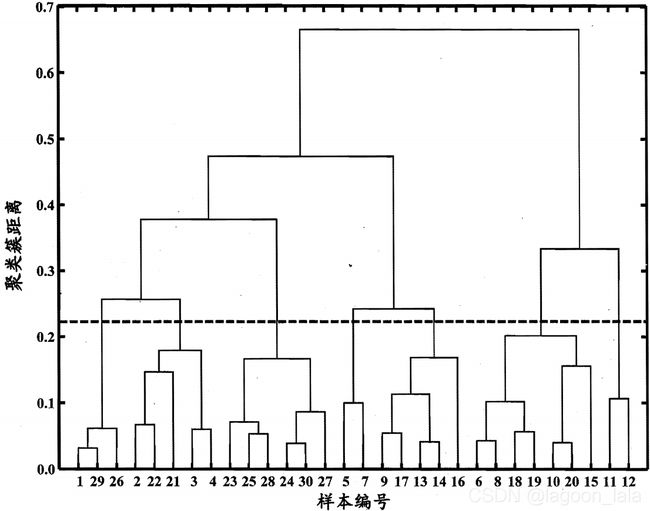
以西瓜数据集4.0为例，令采用d_max的AGNES 算法一直执行到所有样本出现在同一

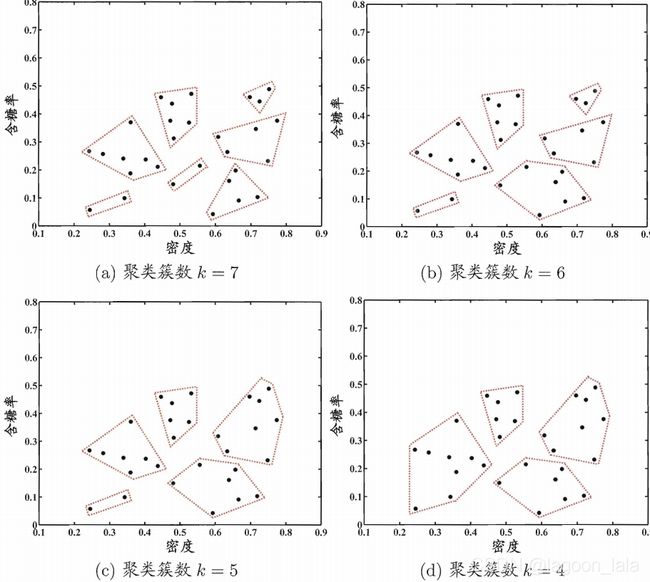
个簇( k=1), 可得"树状图" (dendrogram) ，其中每层链接一组聚类簇. 在树状图的特定层次上进行分割，则可得到相应的簇划分结果(虚线包含7个聚类簇).

对应k= 7, 6, 5, 4时的簇划分结果: