VINS 细节系列 - 初始姿态 g2R() 问题
目录
一、相关概念
二、初始化
重力对齐
理论部分
程序部分
双目加IMU的初始化
理论部分
程序部分
一、相关概念
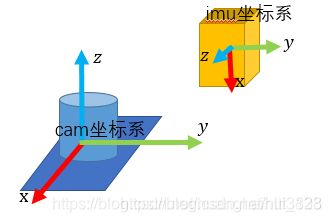
假设有IMU坐标系和相机坐标系如下:
IMU 和 相机有规定其本身的x,y,z轴的方向
1、imu 一般规定右前下分别为x,y,z轴
2、相机一般认为,z轴平行于镜头朝外,x轴与像平面的水平方向一致,从左到右,y轴与像平面垂直方向一致,从上到下
假如: 相机坐标系作为参考坐标系,解算出了 imu坐标系 在 cam坐标系 下的位姿: R ,t
t 代表了平移向量,为imu坐标系原点在相机坐标系的位置;
R 代表的含义可以有以下解释:
- 相机坐标系如何旋转才能转到IMU坐标系 --------- 坐标系的变换
- 表示imu坐标系中的点 通过 这个旋转矩阵 变换到相机坐标系中去 --------- 点的变换
- imu坐标系 在 相机坐标系 的 姿态 (这个更关键,后面会说明白)
注意:坐标系的变换和点的变换是 “相反”的过程;个人感觉这个坐标系转换的概念还是要清晰的!
二、初始化
重力对齐
我们习惯把 第 一帧相机坐标系当作参考坐标系,因为此时的IMU测量的重力加速度还没有进行优化,没有办法与重力加速度 g 对齐,实属无奈之举!
理论部分
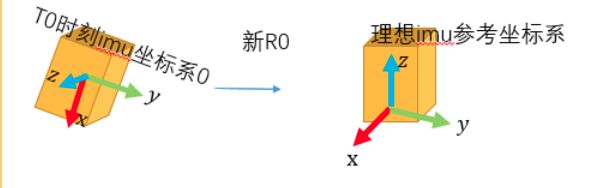
我们用第一次MU测量的加速度 g0 =[-9.4 −2.3 0.4],这时候第一帧imu大概是这个样子,坐标系为 C0
因为程序中,这个加速度 g0 是两帧之间IMU加速度的平均值得到的,故这个IMU坐标系也可以看作第一帧相机坐标系;
假设我们要和理想IMU坐标系重力 g = [0 0 1] 对齐, 参考图如下:
注意:为什么是[0 0 9.8]而不是[0 0 -9.8] ?因为vins的公式推算中,g都是用-号,因此这个相当于是一个朝上的重力
第一部:根据两个向量 g、g0 求出 矩阵R0 (这个是有对应公式的;这里没有t0是因为 他们的原点是一样的,只是为了便于区分,图才分为两个);
R0 便是 C0坐标系在 理想坐标系下的姿态;这里我们想一下,这里的R0仅仅是姿态,我们上一步根据重力对齐求出来了,但是这个姿态在
理想坐标系下还是那种 偏航角 yaw 不是0的状态 ,比如:20度;
有人就会有疑问:C0坐标系下的点 g = R0 ✖g0 , 这个不就对齐了嘛?这个....这个有点偷换概念了, 我也迷糊了一会,还是想通了(自己认为)
我们再看一下第一节中R的概念:
- 相机坐标系如何旋转才能转到IMU坐标系 --------- 坐标系的变换
- 表示imu坐标系中的点 通过 这个旋转矩阵 变换到相机坐标系中去 --------- 点的变换
- imu坐标系 在 相机坐标系 的 姿态 (这个更关键,后面会说明白)
他们是独立的表达,可不能混淆!我们用的是 姿态 这个概念,
(这个可以理解吧,可能会优点迷惑,这个是两个坐标系的相对变化,后面的C1,C2...Cn 他们之间的姿态都是我们要求的,只是会最终转换到C0参考系下)
现在我们想把R0的偏航角yaw 在 理想坐标系中为0,怎么办?很好办呀,求出来,旋转补偿一下就行了,也是后面程序对应的内容!
假设C0绕着理想坐标系的Z轴旋转 -yaw, 对应的矩阵为R1,则 R0 = R1*R0 便是 C0坐标系在理想坐标系下 偏航角为 0的 姿态!
有人又问:为什么偏航角yaw要转换成0 ?自己想吧!
程序部分
/-----------------------------------------------------------------程序---------------------------------------------------------------------/
//初始第一个imu位姿
void Estimator::initFirstIMUPose(vector> &accVector)
{
printf("init first imu pose\n");
initFirstPoseFlag = true;
//计算加速度的均值
Eigen::Vector3d averAcc(0, 0, 0);
int n = (int)accVector.size();
for(size_t i = 0; i < accVector.size(); i++)
{
averAcc = averAcc + accVector[i].second;
}
averAcc = averAcc / n;
printf("averge acc %f %f %f\n", averAcc.x(), averAcc.y(), averAcc.z());
Matrix3d R0 = Utility::g2R(averAcc);
double yaw = Utility::R2ypr(R0).x();
R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;//另初始的航向为0
Rs[0] = R0;
cout << "init R0 " << endl << Rs[0] << endl;
}
子程序 g2R ()
Eigen::Matrix3d Utility::g2R(const Eigen::Vector3d &g)
{
Eigen::Matrix3d R0;
Eigen::Vector3d ng1 = g.normalized();
Eigen::Vector3d ng2{0, 0, 1.0};
R0 = Eigen::Quaterniond::FromTwoVectors(ng1, ng2).toRotationMatrix();
double yaw = Utility::R2ypr(R0).x();
R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;
return R0;
}/-----------------------------------------------------------------程序---------------------------------------------------------------------/
得到的 R0 存入 滑动窗口 的世界坐标系下的旋转 Rs[0];上面我们说的理想坐标系,也是世界坐标系!
所以Ps Vs 是世界坐标系下的位置和速度;Rs (Rw_bk)是 bk 到 w 的转换矩阵!
自己疑问的地方:
double yaw = Utility::R2ypr(R0).x();
R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;
为什么出现两次?还奇怪,想了几个小时,也考到了博客出处的解释,自己有质疑! 本人的解释如下,如有问题还请提出来!
双目加IMU的初始化
理论部分
对陀螺仪bias的校正
程序部分
/-----------------------------------------------------------------程序---------------------------------------------------------------------/
if(STEREO && USE_IMU)
{
//有了深度之后就可以进行PnP求解
f_manager.initFramePoseByPnP(frame_count, Ps, Rs, tic, ric);
// 双目三角化
f_manager.triangulate(frame_count, Ps, Rs, tic, ric);
if (frame_count == WINDOW_SIZE)
{
map::iterator frame_it;
int i = 0;
for (frame_it = all_image_frame.begin(); frame_it != all_image_frame.end(); frame_it++)
{
frame_it->second.R = Rs[i];
frame_it->second.T = Ps[i];
i++;
}
solveGyroscopeBias(all_image_frame, Bgs);
for (int i = 0; i <= WINDOW_SIZE; i++)
{
pre_integrations[i]->repropagate(Vector3d::Zero(), Bgs[i]);
}
optimization();
updateLatestStates(); //让此时刻的值都等于上一时刻的值,用来更新状态
solver_flag = NON_LINEAR;
slideWindow();
ROS_INFO("Initialization finish!");
}
} /-----------------------------------------------------------------程序---------------------------------------------------------------------/