学习...笔记08：Origin绘制常见图像的方法总结

寄蜉蝣于天地，渺沧海之一粟。——苏轼《赤壁赋》

---

前言

夏去秋来，安复一年？为了方便不同专业的读者都能在本文中找到各自所需的内容，本文分为了两大部分：第一部分介绍准备绘图使用的数据，这些数据主要是微磁模拟软件（基于有限差分法）oommf或mumax3生成的，对于其它专业的，不感兴趣的读者可以完全跳过这一部分，无任何障碍的阅读下一部分。本文的第二部分则是总结了使用Origin根据获取到的数据绘制一些常见图像，包括：1.线条图像，2.等高线（热图）图像，3.带箭头的矢量图像，4.带箭头的等高线（热图）图像，5.3D散点图像，6.拼图。在这一部分里详细介绍了每一种图像的特点，绘制方法，以及常见问题。

---

一、获取绘图使用的数据

1.准备磁滞回线的数据

利用oommf自带的示例文件stdprob1.mif来生成本文所需的数据，首先在该文件的Oxs_UZeeman类中追加语句{ -50 0.87275325 0 50 -0.87275325 0 100 }用于使外加磁场的变化是一个完整周期，如此才能形成一条回线。接着在文件末尾追加语句Schedule Oxs_MinDriver::Magnetization archive Done 1用于保存最后一个磁化状态。接着加载该示例文件，并且运行结束后，一共生成了两个文件：.odt和.omf文件。

在这一小节，只对.odt文件进行操作：首先将该文件复制一份然后重命名为loop-Data.txt，然后直接拖到Origin中，Origin会自动加载该文件中所有列。接着需要点击工作表左上方的绿色图标 -----> 删除数据连接器 ，使该工作表变成可编辑状态。在工作表中只保留Oxs_UZeeman::Bx 和 Oxs_MinDriver::mx两列的数据，删除其余列，接着分别将列的长名称命名为“Bx”和“mx” -----> 鼠标右键“Bx”列 ，设置为 “X”；鼠标右键“mx”列 ，设置为 “Y”。 最终工作表为202行，2列。

2.准备标量场平面视图的数据

说到“场”，不得不重温一下有限差分法的基本思想：使用网格将长方体空间范围离散化为一个个尺寸相同的单元格，于是单元格是不可再分的最小空间范围，即认为它是场中的“点”。而代表单元格的空间坐标取值为该单元格的中心位置，举个例子：假设坐标原点在一个长方体空间范围的左下角，向右为+x，向上为+y，平面里为-z，平面外为+z。使用10X10X10nm的网格离散化后，那么表示第一个单元格的空间坐标为(5,5,5)nm，第二个单元格的空间坐标为(15,5,5)nm，注意单元格的顺序是"x->y->z"，按照此规律，只需15个数值就可以保存整个长方体范围内所有单元格的位置坐标，之后再将场里“点”的场值按顺序一行行的存放在文件中，如此便得到了场里每一个“点”的空间坐标和它的场值。这就是我们熟悉的OVF格式，还不熟悉的请参考笔记01，19章。

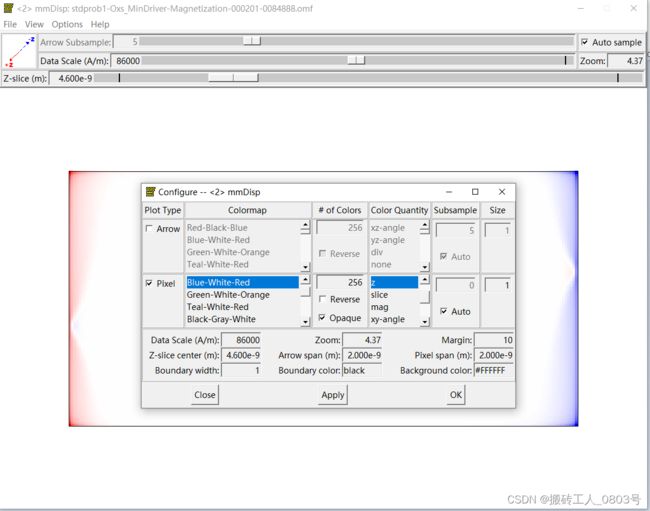
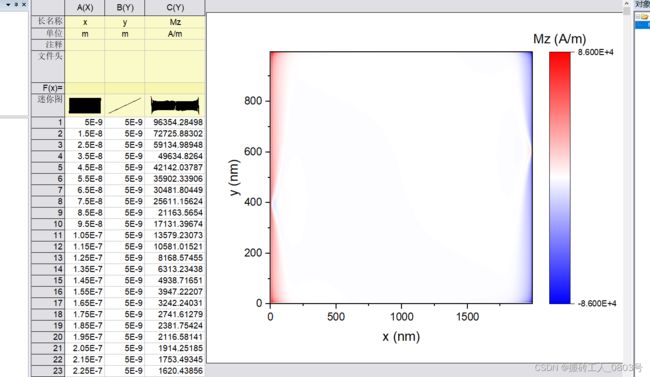
若要使用Origin等第三方绘图软件来绘制每一个单元格的情况下，都需要将单元格的位置坐标列计算出来，即利用oommf的命令行程序avf2odt的-average point参数。本小结对一.1中获取的.omf，其单元格尺寸为10X10X10nm，选择只输出xy平面（切片）的所有单元格（z方向共两层单元格：0-20nm，此处输出第一层：z=0-10nm）使用的命令类似如下：tclsh oommf.tcl avf2odt -average point -region - - 0 - - 10e-9 -ipat TODO_picture\Magnetization.omf -onefile TODO_picture\Magnetization.txt，输出的.txt文件中有六列数据。将生成的.txt文件复制一份并重命名为“pixel-Data.txt”，然后拖进Origin中，删除存放z，M_x，M_y的数据列，只保留了存放单元格x，y坐标的两列，和存放磁化强度的z分量的一列，将三列的长名称命令为：x，y，Mz，单位分别为：m，m，A/m，鼠标右键将三列分别设置为：X，Y，Z。于是该标量场（Mz）平面视图（xy平面）的数据便准备好了，最终工作表有20000行，3列的数据。
使用oommf子程序mmDisplay来显示一.1中获取的.omf文件如下所示（标量场Mz的xy平面视图），待会儿可以和二.2里Origin绘制的图像做一下对比：

3.准备带箭头矢量图的数据

矢量不仅有大小和方向，而且还要有空间坐标来确定矢量放在空间中的位置！对于一个基于有限差分法的矢量场来说，每一个单元格都存放着一个矢量，整个矢量场的直观感受如下面的3D图：

显然，可以用一个二维的带箭头的图来表示这个矢量场的平面视图。首先将一个平面的单元格的矢量都投影在这个平面上（比如xy平面），然后用箭头的长短表示矢量投影在平面上的幅度，箭头的方向表示与x轴的夹角。抽象一点的话就是：在矢量场中单独切出一层单元格，然后一巴掌把这层单元格中的矢量拍平，得到的就是带箭头的矢量图，但是显然，这样丢失了矢量的另一个分量的信息（此处为z分量）。
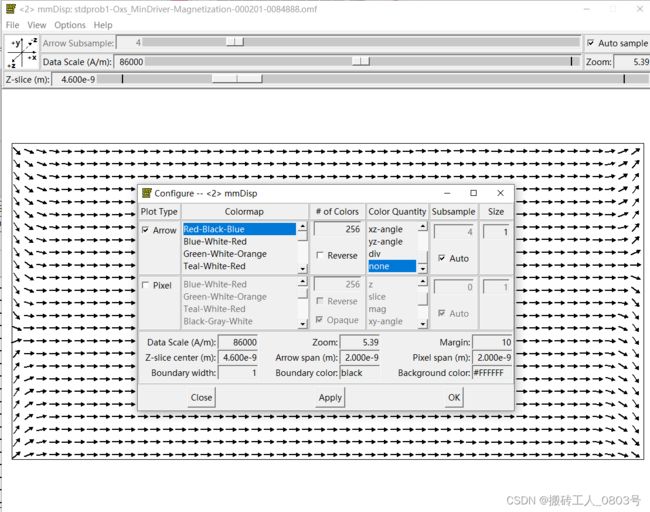
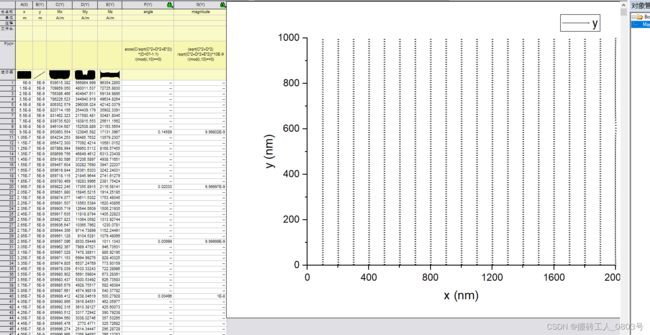
将一.2中生成的带单元格位置坐标列的.txt文件复制一份并重命名为“arrow-Data.txt”，然后直接拖进Origin，在工作表里面，只删除存放z坐标的数据列（xy平面，z是相同的，所以z列无用），按照上一小节的风格命令列的长名称，然后在工作表中末尾新增两列，分别用于存放每一个矢量的角度（长名称：angle）和幅值（长名称：magnitude），这里暂且让这两列为空，将在二.3中讲解如何填充这两列。最后，鼠标右键将存放x坐标的数据列设置为X，将其余列都设置为Y。
使用oommf子程序mmDisplay来显示一.1中获取的.omf文件如下所示（矢量场M的xy平面视图），待会儿可以和二.3里Origin绘制的图像做一下对比（注意此图中箭头的采样率为4，即x和y方向都是间隔4个单元格才显示一个单元格的箭头）：

4.准备矢量场平面视图的数据

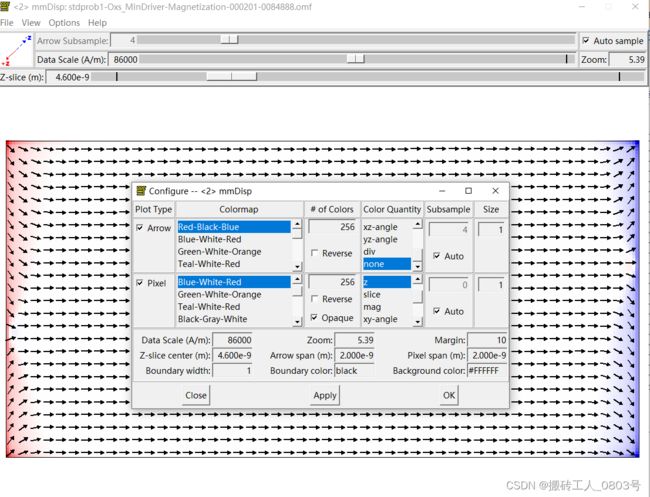
若在二维平面中只使用箭头来表达矢量场平面视图的话，只能表达出它两个分量的信息，但是可以用颜色来映射出第三个分量的信息。矢量场平面视图即是用一个带箭头的矢量图层叠加上一个用颜色映射出第三个分量的等高线图层。如此通过叠加两个图层得到的平面图，可以完全表达出这一层单元格中矢量三个分量的大小。

本小结使用的数据只有二.2和二.3在Origin中生成的 “pixel-Pic”和“arrow-Pic”两张图，无其它数据。
使用oommf子程序mmDisplay来显示一.1中获取的.omf文件如下所示（箭头表示矢量的xy面内分量，颜色表示面外分量），待会儿可以和二.4里Origin绘制的图像做一下对比：

5.准备标量场的数据

有了上文中3D图像中矢量场的直观感受后，对于标量场的理解则更加简单了，无非是把三维图像中的箭头换成带颜色的点就行了。举个好看的示例图片：（出处：DOI: 10.1103/PhysRevApplied.13.034051 ,FIG. 1.）

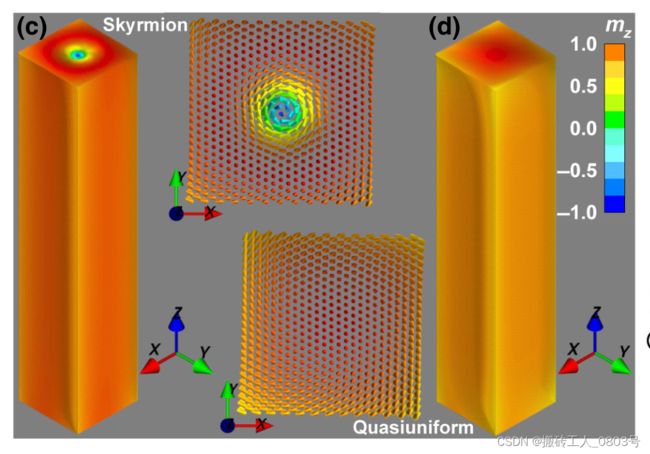
对于一.1中获取的.omf文件，其单元格尺寸为10X10X10nm，本小结选择输出整个空间里的所有单元格，使用的命令类似如下：tclsh oommf.tcl avf2odt -average point -region - - - - - - -ipat TODO_picture\Magnetization.omf -onefile TODO_picture\M.txt，输出的.txt文件中有六列数据。将生成的带单元格位置坐标列的.txt文件复制一份并重命名为“scalarField-Data.txt”，然后直接拖进Origin，在工作表里面，删除存放矢量M的x和y分量的两个数据列，即需要绘制的标量场是Mz(x,y,z)。按照前文的风格命令列的长名称，最后，鼠标右键将存放x坐标的数据列设置为X，将存放y坐标的数据列设置为Y，将存放z坐标的数据列设置为Z，将存放M的z分量的数据列设置为Z。

6.准备拼图的数据

本小结使用的数据为前文Origin中生成的所有图像。

二、Origin绘制一些常见图像

1.线条图像

特点

在该类图像中，从一条曲线上的每一个数据点都可以获取两个数值：横坐标的值和纵坐标的值，表达出的是Y=F(X)的图像。因此需要在Origin的工作表中准备两个数据列：第一列（X）存放每一个数据点的横坐标值，第二列（Y）存放每一个点的纵坐标值。
Origin画线条图像的规律就是：从工作表的第一行获取第一个数据点的横纵坐标值，并在图像中画出该点，从第二行获取第二个数据点的横纵坐标值，并在图像中画出该点，接着使用线段连接这两个相邻的点，以此类推直到画完所有的数据点和线段，于是一条曲线就绘制完成了。若要在同一幅图像中同时绘制多条曲线，就要在工作表中准备多个存放纵坐标值的数据列（Y），且每一个数据点的横坐标列（X）是共用的，即只有一列（X）。

绘制方法

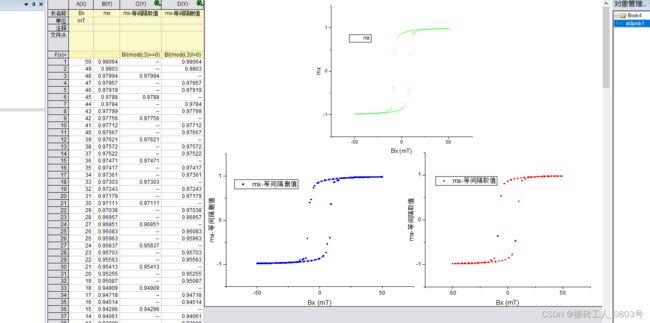
在一.1中生成了磁滞回线所需的数据并复制进了Origin工作表（loop-Data）中：第一列（X）存放的是数据点横坐标的值，长名称“Bx”表示外加磁场的x分量，第二列（Y）存放的是数据点的纵坐标值，长名称“mx”表示归一化磁化强度的x分量。

可以点击左下角工具栏的快捷图标，或者点击菜单栏中的绘图 -----> 基础2D图，折线图 -----> 在图表绘制对话框中，分配数据列：X栏勾选A，Y栏勾选B，确定 -----> 自行手动调节图像的其它外观效果 ，将图像重命名为“loop-pic” -----> 打开原工作表，空白处右键 -----> 添加图形窗口，选中绘制完成的图像，确定。

常见问题

Origin学习版的一个项目最多只有12个可用的工作簿和图像，多余的被锁住了，怎么办？

由于学习版的功能受限，所以我们只能优化自己的文件结构：①合并多个工作表到同一个工作簿中。在打开的工作簿界面的左下角鼠标右键 -----> 插入，来生成一个新的工作表。将同类型的数据插入到同一个工作簿的多个工作表中可以显著减少工作簿数量。②拆分原来大的项目，生成多个新的小项目来保存大量文件。对象管理器栏目中：在大的项目的顶层目录里面新建一个临时目录，将需要迁移的文件全部拖进该文件夹中，鼠标右键该文件夹 -----> 保存为项目文件 ，确定保存 -----> 在新建的项目里，鼠标右键项目名称 -----> 追加项目，选择保存的项目文件并确定。于是文件便从一个项目迁移到了另一个项目。

图像中的数据点太多，在Origin工作表中如何对数据列设置取样间隔，等间隔绘制点以便减少数据点？

在Origin工作表中的数据列的填充公式里加入取模运算，可以很方便的实现等间隔采样数据点。原理是：列的填充公式里面表示行号的变量为“i”，列的变量为该列的字母，工作表中的单元格中除以0之后都会变成符号“–”，即该单元格的值变为空值了。
以上文的工作表为例，间隔2个数据点绘制。首先工作表新增一列“C”，在其填充公式F(x)里输入B/(mod(i,3)==0)，于是当Origin为“C”列第一行取值时，式子(mod(1,3)==0)显然等于0，于是“C”列第一行值为B列第一行的值除以0，结果为“–”，第二行时，式子(mod(2,3)==0)显然也等于0，于是结果也为“–”，直到第三行时，式子(mod(3,3)==0)等于1，于是B列第三行的值除以1，结果就是B列第三行的值，以此规律算出“C”列的所有行。同理，按此原理也可以轻松实现等间隔“剔除”Origin工作表中的数据点，即把条件语句mod(i,3)==0改成mod(i,3)!=0，于是就实现了每间隔两个数据点就删除一个数据点的效果。绘制散点图来直观对比一下这三种的效果：

画出的单条曲线出现头尾相连，相交的情况？

通常存放数据点横坐标的X列是按照升序排列的，否则画出的线条会出现交叉，闭合的情况。若需要避免出现这些情况时，则需要重新排序，在Origin菜单栏的工作表选项中选择排序方式，重新按照横坐标列升序即可。当然若绘制的是散点图，则没有这种升序要求。

2.等高线（热图）图像

特点

从这类图像中的每一个点可以获取三个数值：该点的横坐标、纵坐标、和该点的数值（用颜色表示，映射关系从配套的色条读取），表达出的是Z=F(X,Y)的图像。因此在工作表中也相应的准备三列数据：X列存放数据点的横坐标，Y列存放数据点的纵坐标，Z列存放数据点的值。Origin绘图时会从工作表的第一行开始，依次获取每一个数据点的横、纵坐标和该点的值，在图像中根据坐标找到位置后使用颜色表达出该数据点的值，至于数据点与数据点之间的间隔区域则自动使用渐变颜色来填充，因此对于工作表中存放坐标的X和Y列是没有排序要求的。

绘制方法

在一.2中Origin工作表（pixel-Data）存放的是标量场Mz的xy平面视图的数据：第一列（X）存放的是数据点横坐标的值，长名称“x”，第二列（Y）存放的是数据点纵坐标的值，长名称“y”，第三列（Z）存放的是数据点的值，长名称“Mz”表示磁化强度的z分量。

点击菜单栏中的绘图 -----> 等高线图，等高线图-颜色填充 -----> 在图表绘制对话框中，分配数据列：X栏勾选A，Y栏勾选B，Z栏勾选C，确定 -----> 双击图像，颜色映射/等高线选项卡中 -----> 线：隐藏所有，于是图中的等高线消失；填充：三色有限填充，从蓝到白到红；级别：从-86000到86000，主级别数25，次级别数9，级别总数自动变成256 -----> 关闭快速模式 -----> 自行手动调节图像和色条的其它效果直到适合 ，将图像重命名为“pixel-Pic” -----> 打开原工作表，空白处右键 -----> 添加图形窗口，选中绘制完成的图像，确定。

常见问题

如何使图像中的颜色差异变大，即更容易区分出取值接近的点？

在颜色映射/等高线选项卡中：减少颜色映射的范围，对于超出级别范围的，则使用和最小，最大值的相同颜色映射。比如本例中，Mz原来的最大取值范围是-860000到860000，但为了增大颜色差异，便把最大取值范围缩小到了-86000到86000，对于<-86000的使用蓝色填充（和最小值的颜色相同），对于>86000的使用红色填充（和最大值的颜色相同）。

3.带箭头的矢量图像

特点

从这类图像中的每一个箭头可以获取四个数值：该箭头的横坐标、纵坐标、箭头的角度、箭头的长度，表达出的是矢量场的平面视图（其实只能表达出矢量的两个分量）。因此在工作表中也相应的准备四列数据：X列存放箭头的横坐标，第一个Y列存放箭头的纵坐标，第二个Y列存放箭头的旋转角度，第三个Y列存放箭头的长度，于是工作表中每一行就代表了绘制一个单独的箭头所需的信息。

在一.3中Origin工作表（arrow-Data）存放的是矢量场M的xy平面视图的数据：第一列（X）存放的是箭头的横坐标，长名称“x”；第二列（Y）存放的是箭头的纵坐标，长名称“y”；第三列（Y）存放的是矢量场M的x分量，长名称“Mx”；第四列（Y）存放的是矢量场M的y分量，长名称“My”；第五列（Y）存放的是矢量场M的z分量，长名称“Mz”；第六列（Y）存放的箭头的旋转角度，还未填充，为空，长名称“angle”；第七列（Y）存放箭头的长度，还未填充，为空，长名称“magnitude”。接下来我们通过每一个矢量的三个分量来计算每一个箭头的旋转角度和箭头长度，本小结以绘制xy平面的箭头为例，其它平面则方法类似：
①箭头的旋转角度：
两个矢量之间的夹角有关系式：$cos\theta =\frac{M\cdot e_x}{|M||e_x|}$，利用这个式子和反三角函数"acos"可以很轻松算出矢量与x轴之间的夹角，所以在角度列的填充公式F(x)里写入acos(C/sqrt(C^2+D^2+E^2))*(D<0?-1:1)，其中*(D<0?-1:1)表示矢量的y分量若小于0，则乘以-1，否则乘以1。这是因为acos得到的旋转角度只有范围0到$\pi$，无法区分箭头指向+y还是-y，所以增加了对矢量的y分量的判断式子。
②箭头的长度：
很简单，矢量 $M$ 投影在xy平面上的长度为：$\sqrt{{M_x}^2+{M_y}^2}$，但通常我们需要对它进行归一化处理方便绘图，使箭头的最大长度为图像中两个箭头中心点之间的距离。此处两个箭头之间间隔为10e-9m，所以在该列的F(x)中填入(sqrt(C^2+D^2)/sqrt(C^2+D^2+E^2))*10e-9。
最后由于工作表中存放了20000个箭头的绘图数据，实在是太密集了，于是在这两列的公式后面追加/(mod(i,10)==0)以降低10倍箭头数量。

绘制方法

点击菜单栏中的绘图 -----> 专业图，XYAM矢量图 -----> 在图表绘制对话框中，分配数据列：X栏勾选“x”，Y栏勾选"y"，A栏勾选"angle"，M栏勾选"magnitude"，确定 -----> 双击坐标轴，修改坐标轴范围：x轴为0到2e-6，y轴为0到1e-6，修改其它轴相关的选项 -----> 双击图像中的箭头 -----> 矢量选项卡中：箭头-长度10；大小-乘数1，现实大小；位置-中点 -----> 关闭快速模式 -----> 自行手动调节图像的其它效果直到适合 ，将图像重命名为“arrow-Pic” -----> 打开原工作表，空白处右键 -----> 添加图形窗口，选中绘制完成的图像，确定。

常见问题

如何单独降低横向或者纵向的箭头数量，使整个图像的箭头看起来更稀疏，更清爽？

这个问题可以在Origin的工作表中对箭头的两个坐标列进行取模运算，剔除多余的数据点解决。不过最好是在生成矢量场的数据时就加入采样率，避免后续在工作表中各种运算。

4.带箭头的等高线（热图）图像

特点

从这类图像中的每一个箭头处可以获取五个数值：该箭头的横坐标、纵坐标、箭头的角度、箭头的长度，和该箭头图层下方位置处的颜色，表达出的是矢量场的平面视图（完全表达出了该位置处矢量的三个分量值）。
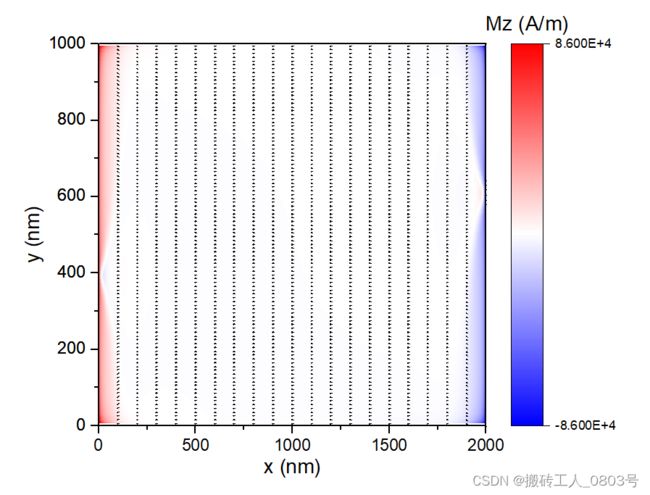
在二.2中绘制了用颜色来映射出矢量的一个分量的等高线图“pixel-Pic”，在二.3中绘制了用箭头表达矢量的两个分量的XYAM图“arrow-Pic”，所以要完全表达出了矢量的三个分量值，则需要将这两个图像叠加起来形成一个新的图像。

绘制方法

在叠加两个图像之前，可以先将它们的坐标轴调节成相同的，然后激活两个图中的任意一个 -----> 菜单栏，图，合并图表，打开对话框 -----> 勾选自动预览 -----> 排列设置：行数和列数都设为1 -----> 确定，并将新图重命名“magnetization” -----> 删除图像中重叠的坐标轴，手动调节其它显示选项直到适合。

常见问题

有两个空间范围相同，且网格尺寸相同的矢量场（基于有限差分法）文件，在Origin中如何对这两个矢量场做点乘运算，从而生成一个标量场文件？

根据矢量的点乘公式：$M\cdot H=M_x{H}_x+M_y{H}_y+M_z{H}_z$，和保存矢量场的OVF文件格式，可以将这两个保存着矢量场的OVF文件拖进Origin的两个工作表中，即表1和表2（行数是相同的），于是每一个工作表都有三列数据，分别存放矢量场的三个分量。接着再新建一个只有一列的工作表，即表3，在该列的填充公式F(x)中填入矢量的点乘公式，即用 表1的第一列乘以表2的第一列 + 表1的第二列乘以表2的第二列 + 表1的第三列乘以表2的第三列。如此表3的行数和表1和表2是相同的。最后可以将表3保存为一个文件，并根据OVF文件格式来手动填写文件头的注释信息。

5.3D散点图像

特点

三维图像通常用于直观的表达“物理场”，而3D散点图像显然适合用于表达标量场，从这类图像中的每一个点可以获取四个数值：该点的x坐标、y坐标、z坐标、点的颜色表示该点的值。因此在工作表中也相应的准备四列数据：X列存放点的x坐标，Y列存放点的y坐标，第一个Z列存放点的z坐标，第二个Z列存放点的值，于是每一行就代表了绘制一个点所需的信息。那么Origin在绘制3D图像时，从工作表的第一行开始，先根据点的三个坐标列在三维图像中定位该点，然后根据四列存放的值来使用颜色来映射来绘制该点。

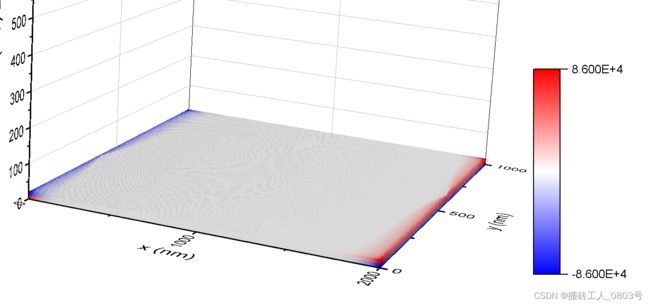
在一.5中Origin工作表（scalarField-Data）存放的是标量场Mz的数据：第一列（X）存放的是场中每一个点的x坐标，长名称“x”；第二列（Y）存放的是点的y坐标，长名称“y”；第三列（Z）存放的是点的z坐标，长名称“z”；第四列（Z）存放的是该点的值，长名称“Mz”。

绘制方法

点击菜单栏中的绘图 -----> 3D，3D散点图 -----> 图表绘制对话框中：X栏勾选“x”，Y栏勾选"y"，Z栏勾选“z” ，确定 -----> 双击图像，打开绘图细节对话框 -----> 符号选项卡 ：符号-立方体，大小5，颜色-按点-颜色映射Mz -----> 颜色映射选项卡：填充-3色有限填充，从蓝到白到红；级别-从-86000到86000，主级别数25，次级别数9，级别总数自动变成256 ，超出级别范围的颜色映射与最大和最小级别颜色相同 -----> 手动删除图例，在页面左方工具栏中点击添加颜色标尺 -----> 双击坐标轴，调整z轴的范围为0到1e-6 -----> 手动调节图像的其它显示选项直到适合 -----> 重命名图像为“scalarField-Pic”

常见问题

画出的3D散点图只是在某个轴方向太稀疏怎么办？

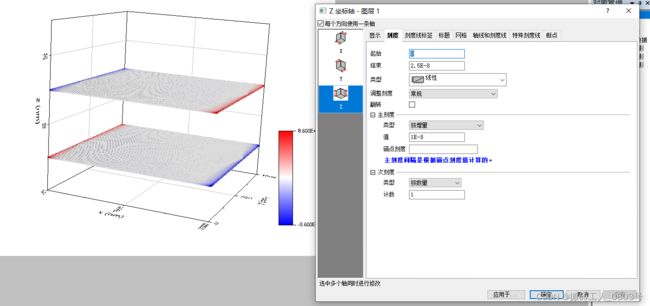
在不修改散点的形状大小的情况下，可以增大坐标轴的显示范围，因为视角拉的越远，散点图之间的间距就越小，视角拉的越近，散点图之间的间距就会越明显。比如本例中，将z轴的范围减少为2.5e-8，于是在z方向相当于拉进了视角：

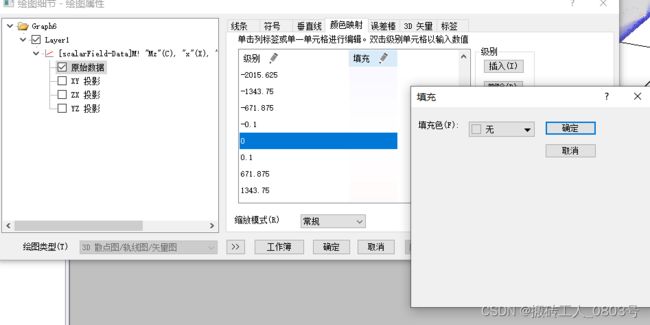
对于标量值在0周围的数据点而言，在3D散点图中的颜色不能显著区分0和接近于0的情况。

颜色映射选项卡：在级别0的上下处，手动插入级别，并双击0上面的新级别，修改为0.1，颜色映射为白色（替代0的颜色），双击0下面的新级别，修改为-0.1，颜色映射为白色（替代0的颜色），最后，将0的颜色设为无，如下所示：

如何表达出更多维度的数据？

参考Origin帮助文档： FAQ-184 如何在 Origin 中绘制四维（4D）图形数据？
“，，，基于这种使用颜色来表现第四维信息的思路，我们可以进一步拓展，从而在一幅 3D XYZ 图中表现出多达八维的数据信息，，，”

6.拼图

特点

将多张子图组合在一起，使用字母序号标记每一个子图，组成一个大图。
前文已经使用Origin生成了5张图片：“loop-pic”，“pixel-Pic”，“arrow-Pic”，“magnetization”，“scalarField-Pic”，接下来使用Origin的布局功能来组合这5张图片。

绘制方法

点击菜单栏中的文件，新建，布局 -----> 菜单栏格式，布局页面，单位-厘米，只固定宽度15 -----> 在页面中鼠标右键，添加图形窗口 -----> 将以上5个图依次添加完 -----> 调节图像大小，利用页面的对齐工具进行对齐。

关于拼图更详细的步骤可以参考官方教程链接。

常见问题

布局中子图调整大小，对齐的技巧？

在布局中对子图调整时，可以先将一个子图的尺寸和位置固定好，右键图像，修改其属性，使其大小，位置不可变。然后以这个子图作为参照物，先鼠标点击该子图，再按住ctrl并同时选中其他子图，然后再使用工具栏的对齐和调整大小等其他功能进行操作。

总结

本文总结了线图，等高线图，带箭头的矢量图，带箭头的等高线（热图）图，3D散点图像，拼图的特点，绘制方法，以及绘制时的常见问题，相较于其它Origin的视频教程，使用文字终究难以表述清楚画图软件的操作，不过Origin是很容易上手的，绘制图像也是十分方便的，终归是熟能生巧的。

最后，如果觉得本文对你有帮助的话，可以在下方点个赞！