鲁鹏老师三维重建课程之单视图重建

配置Json环境

       使用Jsoncpp包中的.cpp和 .h文件
       解压上面下载的 Jsoncpp 文件，把 jsoncpp-src-0.5.0文件拷贝到工程目录下， 将 jsoncpp-src-0.5.0\jsoncpp-src-0.5.0\include\json 和 jsoncpp-src-0.5.0\jsoncpp-src-0.5.0\src\lib_json 目录里的文件包含到VS工程中，在VS工程的属性C/C++下General中 Additional Include Directories 包含头文件目录 .\jsoncpp-src-0.5.0\include 。在使用的cpp文件中 包含json头文件即可，如： #include "json/json.h" 。将 json_reader.cpp、 json_value.cpp和 json_writer.cpp三个文件的Precompiled Header属性设置为 Not Using Precompiled Headers， 否则编译会出现错误。

试了很多方法，上述方法亲测可用。

准备工作

读图解析Json文件及声明变量

    Mat src = imread(".//images//chessboard.jpg");
	//声明一些存储直线点的变量
	int i=0;
	vector < vector > Points;
	vector XZ_line, YZ_line, XY_line, XZ_line1, YZ_line1, XY_line1;
	Points.push_back(XZ_line);
	Points.push_back(YZ_line);
	Points.push_back(XY_line);
	Points.push_back(XZ_line1);
	Points.push_back(YZ_line1);
	Points.push_back(XY_line1);
	Point2d orignPoint;
	//第一步先解析Json数据
	//用来判断是线还是交点的点
	string shape_type = "line";
	//用来区分线条的类型
	vector linetype;
	string c = ",";
	linetype.push_back("XZ_line");
	linetype.push_back("YZ_line");
	linetype.push_back("XY_line");
	linetype.push_back("XZ_line'");
	linetype.push_back("YZ_line'");
	linetype.push_back("XY_line'");
    //声明读取Json文件变量
	Json::Reader reader;
	Json::Value root;
	ifstream in(".//labelme_data//chessboard_line.json", ios::binary);
	if (!in.is_open())
	{
		cout << "打开文件错误\n";
		return 0;
	}
	if (reader.parse(in,root))
	{
		int temp = root["shapes"].size();
		for (int m =0; m < temp; m++)
		{
			string shapetype = root["shapes"][m]["shape_type"].asString();
			//判断是否为直线点，还是交点
			if (shapetype == shape_type)
			{
				string templinetype = root["shapes"][m]["label"].asString();
				for (; i < linetype.size(); i++)
				{
					if (templinetype == linetype[i])
					{
						//得到points标签下的数据（此时为string类型）
						int temppointsize = root["shapes"][m]["points"].size();
						for (int j = 0; j < temppointsize; j++)
						{
							string strpoint = root["shapes"][m]["points"][j].toStyledString();
							//对读取到的字符串进行处理，删除[]和空格字符
							strpoint.erase(strpoint.find(' '),1);
							strpoint.erase(strpoint.find('['), 1);
							strpoint.erase(strpoint.find(' '), 1);
							strpoint.erase(strpoint.find(']'), 1);
							//将该字符串按逗号分割
							vector res;
							SplitString(strpoint, res, c);
							//将字符串转为double
							Point2d temppoint;
							temppoint.x = atof(res[0].c_str());
							temppoint.y = atof(res[1].c_str());
							Points[i].push_back(temppoint);
						}
						
					}
				}
				i = 0;
			}
			//原点位置
			else if (shapetype == "point")
			{
				//得到points标签下的数据（此时为string类型）
				string strpoint = root["shapes"][m]["points"].toStyledString();
				//对读取到的字符串进行处理，删除[]和空格字符
				strpoint.erase(strpoint.find(' '), 1);
				strpoint.erase(strpoint.find('['), 1);
				strpoint.erase(strpoint.find('['), 1);
				strpoint.erase(strpoint.find(' '), 1);
				strpoint.erase(strpoint.find(']'), 1);
				strpoint.erase(strpoint.find(']'), 1);
				//将该字符串按逗号分割
				vector res;
				SplitString(strpoint, res, c);
				//将字符串转为double
				orignPoint.x = atof(res[0].c_str());
				orignPoint.y = atof(res[1].c_str());
			}

		}
		in.close();

	}

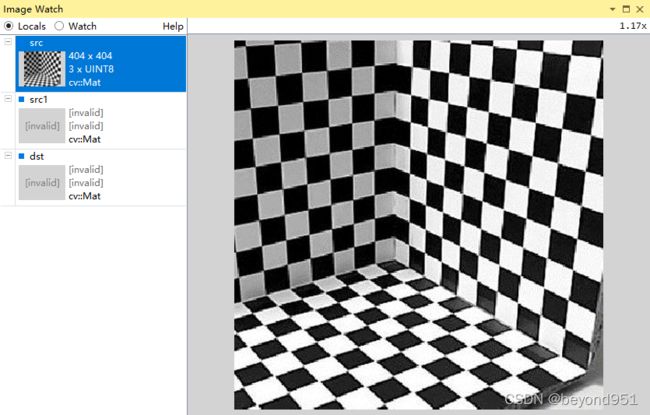
读取到的图像如下：

 将Json文件里面标记的直线和点加载到图片上，并绘制出来可视化

    //点读取完毕，根据点将线条画在图上
	//复制一张图像
	//YZ_line, XY_line, XZ_line1, YZ_line1, XY_line1;
	Mat src1 = src.clone();
	for (int k = 0; k < Points.size(); k++)
	{
		int tempSize = Points[k].size()/2;
		for (int n = 0; n < tempSize; n++)
		{
			switch (k)
			{
			case 0:
				line(src1, Points[k][2 * n], Points[k][2 * n + 1], Scalar(0, 0, 255), 1);
				XZ_line.push_back(Points[k][2 * n]);
				XZ_line.push_back(Points[k][2 * n+1]);
				break;
			case 1:
				line(src1, Points[k][2 * n], Points[k][2 * n + 1], Scalar(0, 255, 0), 1);
				YZ_line.push_back(Points[k][2 * n]);
				YZ_line.push_back(Points[k][2 * n + 1]);
				break;
			case 2:
				line(src1, Points[k][2 * n], Points[k][2 * n + 1], Scalar(255, 0, 0), 1);
				XY_line.push_back(Points[k][2 * n]);
				XY_line.push_back(Points[k][2 * n + 1]);
				break;
			case 3:
				line(src1, Points[k][2 * n], Points[k][2 * n + 1], Scalar(0, 255, 255), 1);
				XZ_line1.push_back(Points[k][2 * n]);
				XZ_line1.push_back(Points[k][2 * n + 1]);
				break;
			case 4:
				line(src1, Points[k][2 * n], Points[k][2 * n + 1], Scalar(255, 255, 0), 1);
				YZ_line1.push_back(Points[k][2 * n]);
				YZ_line1.push_back(Points[k][2 * n + 1]);
				break;
			case 5:
				line(src1, Points[k][2 * n], Points[k][2 * n + 1], Scalar(255, 0, 255), 1);
				XY_line1.push_back(Points[k][2 * n]);
				XY_line1.push_back(Points[k][2 * n + 1]);
				break;
			default:
				break;
			}
			
		}

	}

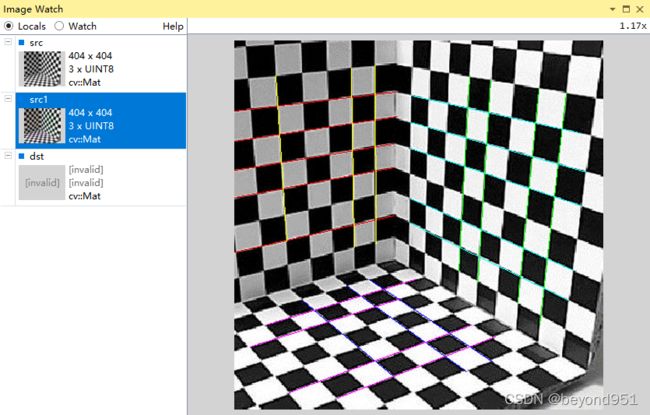
加载完，不同平面的直线用不同颜色绘制的直线和点如下图所示：

 计算影消点

计算影消点，就是根据上面各个平面平行的直线，拟合出平行直线的交点。平行的直线本该没有交点，但经过摄影几何的透视变换，现实世界坐标系下的平行线都会相交于一点，这个点就是影消点，也就是世界坐标系里面的无穷远点，两条平行直线相交于无穷远处。但在摄影几何下，经过透视变换，无穷远点变为影消点，影消点在图像坐标系下可以求。

无穷远点变为影消点最直观的例子，拍摄一条火车铁轨，铁轨最终在图像里面一个点相交。

    //接下来求图像上的影消点
	//即计算两个平面平行线的交点
	//先计算XZ平面，两条平行线的交点
	//计算出来的line为Vec4f类型，即line[0-3]
	//斜率为line[1]/line[0],并过点(line[2],line[3])
	//先将其转为向量相乘的形式即l·x=0的形式，这里l其实为l的转置
	//l为(line[1],-line[0],-line[1]*line[2]+line[0]*line[3])
	vector vecLineXZ;
	vector vecLineYZ;
	vector vecLineXY;
	vector vecLineXZ1;
	vector vecLineYZ1;
	vector vecLineXY1;
	for (int i = 0; i < vecXZLine.size(); i++)
	{
		Vec3d tempvec;
		tempvec[0] = vecXZLine[i][1];
		tempvec[1] = -vecXZLine[i][0];
		tempvec[2] = -vecXZLine[i][1] * vecXZLine[i][2] + vecXZLine[i][0] * vecXZLine[i][3];
		vecLineXZ.push_back(tempvec);
	}
	for (int i = 0; i < vecYZLine.size(); i++)
	{

		Vec3d tempvec;
		tempvec[0] = vecYZLine[i][1];
		tempvec[1] = -vecYZLine[i][0];
		tempvec[2] = -vecYZLine[i][1] * vecYZLine[i][2] + vecYZLine[i][0] * vecYZLine[i][3];
		vecLineYZ.push_back(tempvec);
	}
	for (int i = 0; i < vecXYLine.size(); i++)
	{
		Vec3d tempvec;
		tempvec[0] = vecXYLine[i][1];
		tempvec[1] = -vecXYLine[i][0];
		tempvec[2] = -vecXYLine[i][1] * vecXYLine[i][2] + vecXYLine[i][0] * vecXYLine[i][3];
		vecLineXY.push_back(tempvec);
	}
	for (int i = 0; i < vecXZ1Line.size(); i++)
	{
		Vec3d tempvec;
		tempvec[0] = vecXZ1Line[i][1];
		tempvec[1] = -vecXZ1Line[i][0];
		tempvec[2] = -vecXZ1Line[i][1] * vecXZ1Line[i][2] + vecXZ1Line[i][0] * vecXZ1Line[i][3];
		vecLineXZ1.push_back(tempvec);
	}
	for (int i = 0; i < vecYZ1Line.size(); i++)
	{

		Vec3d tempvec;
		tempvec[0] = vecYZ1Line[i][1];
		tempvec[1] = -vecYZ1Line[i][0];
		tempvec[2] = -vecYZ1Line[i][1] * vecYZ1Line[i][2] + vecYZ1Line[i][0] * vecYZ1Line[i][3];
		vecLineYZ1.push_back(tempvec);
	}
	for (int i = 0; i < vecXY1Line.size(); i++)
	{
		Vec3d tempvec;
		tempvec[0] = vecXY1Line[i][1];
		tempvec[1] = -vecXY1Line[i][0];
		tempvec[2] = -vecXY1Line[i][1] * vecXY1Line[i][2] + vecXY1Line[i][0] * vecXY1Line[i][3];
		vecLineXY1.push_back(tempvec);
	}
	//求XZ平面的影消点
	Vec3d testVanishPoint = RobertColins(XZ_line, src.cols, src.rows);

	Vec3d pointvanishXZvec = vecLineXZ[0].cross(vecLineXZ[vecLineXZ.size() - 1]);
	//将齐次点形式转为欧式坐标
	Point2d pointvanishXZ = Point2d(pointvanishXZvec[0] / pointvanishXZvec[2], pointvanishXZvec[1] / pointvanishXZvec[2]);
	//将图片放大，将影消点可视化
	Mat dst(6060, 6060, CV_8UC3, Scalar(255, 255, 255));
	Rect roiRect = Rect(2827, 2827, src.cols, src.rows);
	src1.copyTo(dst(roiRect));
	//定义偏移量
	Point2d dispoint = Point2d(2828, 2828);
	line(dst, XZ_line[0] + dispoint, pointvanishXZ + dispoint, Scalar(0, 0, 255), 1);
	line(dst, XZ_line[XZ_line.size() - 1] + dispoint, pointvanishXZ + dispoint, Scalar(0, 0, 255), 1);
	//求YZ平面的影消点
	Vec3d pointvanishYZvec = vecLineYZ[0].cross(vecLineYZ[vecLineYZ.size() - 1]);
	Point2d pointvanishYZ = Point2d(pointvanishYZvec[0] / pointvanishYZvec[2], pointvanishYZvec[1] / pointvanishYZvec[2]);
	line(dst, YZ_line[1] + dispoint, pointvanishYZ + dispoint, Scalar(0, 255, 0), 1);
	line(dst, YZ_line[YZ_line.size() - 1] + dispoint, pointvanishYZ + dispoint, Scalar(0, 255, 0), 1);
	//求XY平面的影消点
	Vec3d pointvanishXYvec = vecLineXY[0].cross(vecLineXY[vecLineXY.size() - 1]);
	Point2d pointvanishXY = Point2d(pointvanishXYvec[0] / pointvanishXYvec[2], pointvanishXYvec[1] / pointvanishXYvec[2]);
	line(dst, XY_line[1] + dispoint, pointvanishXY + dispoint, Scalar(255, 0, 0), 1);
	line(dst, XY_line[XY_line.size() - 1] + dispoint, pointvanishXY + dispoint, Scalar(255, 0, 0), 1);
	//求XZ'平面的影消点
	Vec3d pointvanishXZ1vec = vecLineXZ1[0].cross(vecLineXZ1[vecLineXZ1.size() - 1]);
	Point2d pointvanishXZ1 = Point2d(pointvanishXZ1vec[0] / pointvanishXZ1vec[2], pointvanishXZ1vec[1] / pointvanishXZ1vec[2]);
	line(dst, XZ_line1[0] + dispoint, pointvanishXZ1 + dispoint, Scalar(0, 255, 255), 1);
	line(dst, XZ_line1[XZ_line1.size() - 1] + dispoint, pointvanishXZ1 + dispoint, Scalar(0, 255, 255), 1);
	//求YZ'平面的影消点
	Vec3d pointvanishYZ1vec = vecLineYZ1[0].cross(vecLineYZ1[vecLineYZ1.size() - 1]);
	Point2d pointvanishYZ1 = Point2d(pointvanishYZ1vec[0] / pointvanishYZ1vec[2], pointvanishYZ1vec[1] / pointvanishYZ1vec[2]);
	line(dst, YZ_line1[1] + dispoint, pointvanishYZ1 + dispoint, Scalar(255, 255, 0), 1);
	line(dst, YZ_line1[YZ_line1.size() - 1] + dispoint, pointvanishYZ1 + dispoint, Scalar(255, 255, 0), 1);
	//求XY'平面的影消点
	Vec3d pointvanishXY1vec = vecLineXY1[0].cross(vecLineXY1[vecLineXY1.size() - 1]);
	Point2d pointvanishXY1 = Point2d(pointvanishXY1vec[0] / pointvanishXY1vec[2], pointvanishXY1vec[1] / pointvanishXY1vec[2]);
	line(dst, XY_line1[1] + dispoint, pointvanishXY1 + dispoint, Scalar(255, 0, 255), 1);
	line(dst, XY_line1[XY_line1.size() - 1] + dispoint, pointvanishXY1 + dispoint, Scalar(255, 0, 255), 1);
	//至此，各个平面的影消点都已求出来
	//根据XZ、YZ、XY平面的影消点，进行相机内参标定，求解W矩阵
	vector vanishPointVec;
	vanishPointVec.push_back(pointvanishXZ);
	vanishPointVec.push_back(pointvanishYZ);
	vanishPointVec.push_back(pointvanishXY);


	return 0;
}

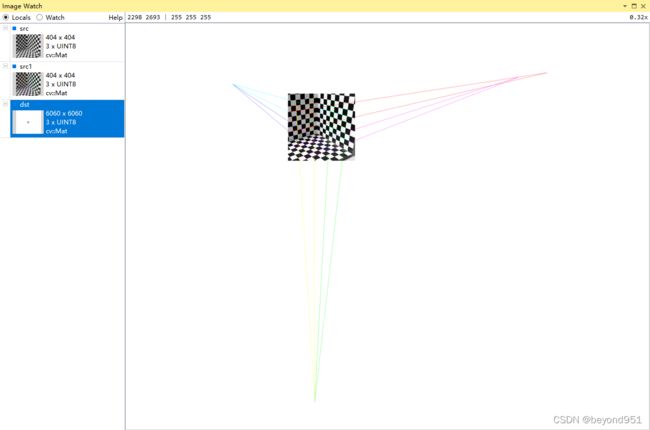
求得影消点的图片如下图所示：

 计算影消点时，用到了柯林斯算法，该算法如下：

//罗伯特·柯林斯方法求影消点
//输入参数为直线的端点，图像的宽高
//输出为影消点的齐次坐标形式
Vec3d RobertColins(vector vecLinePoints,int cols,int rows)
{
	Vec3d vanishPoint;
	int size = vecLinePoints.size();
	//防止坐标点差异过大造成求解精度下降，进行偏移
	int offset = (cols + rows) / 4;
	//这里直线端点，以两个点为一组代表一条直线
	//因此size必为偶数
	//得出各条直线的方向向量
	vector  Lines;
	for (int i = 0; i < size/2; i++)
	{
		Vec3d startPoint, endPoint;
		startPoint[0] = (vecLinePoints[2 * i].x-offset);
		startPoint[1] = (vecLinePoints[2 * i].y-offset);
		startPoint[2] = offset;
		endPoint[0] = (vecLinePoints[2 * i + 1].x - offset);
		endPoint[1] = (vecLinePoints[2 * i + 1].y - offset);
		endPoint[2] = offset;
		//两个点坐标向量的叉乘等于，过该两点的直线齐次坐标向量
		Lines.push_back(startPoint.cross(endPoint));
	}
	/*声明一个Mat M形成3×3的“二阶矩”矩阵M为
	        [a_i*a_i        a_i*b_i        a_i*c_i]
	M = sum [a_i*b_i        b_i*b_i        c_i*b_i]
		    [a_i*c_i        b_i*c_i        c_i*c_i]
	其中取i = 1到n的和。注意，M是对称矩阵。*/
	Mat M = (Mat_(3, 3)<<0,0,0,0,0,0,0,0,0);
	for (int i = 0; i < size / 2; i++)
	{
		Mat tempM = (Mat_(3, 3));
		tempM.at(0, 0) = Lines[i][0] * Lines[i][0];
		tempM.at(0, 1) = Lines[i][0] * Lines[i][1];
		tempM.at(0, 2) = Lines[i][0] * Lines[i][2];

		tempM.at(1, 0) = Lines[i][1] * Lines[i][0];
		tempM.at(1, 1) = Lines[i][1] * Lines[i][1];
		tempM.at(1, 2) = Lines[i][1] * Lines[i][2];

		tempM.at(2, 0) = Lines[i][2] * Lines[i][0];
		tempM.at(2, 1) = Lines[i][2] * Lines[i][1];
		tempM.at(2, 2) = Lines[i][2] * Lines[i][2];

		M = M + tempM;
	}
	//对M矩阵进行特征值分解
	Mat eigenvector = (Mat_(3, 3));
	Mat eigenvalue = (Mat_(3, 1));
	eigen(M, eigenvalue, eigenvector);
	vanishPoint[0] = eigenvector.at(0, 2)*(offset / (eigenvector.at(0, 2))) + offset;
	vanishPoint[1] = eigenvector.at(1, 2)*(offset / (eigenvector.at(0, 2))) + offset;
	vanishPoint[2] = 1;
	return vanishPoint;
}

解析Json文件用到的字符串处理方法：

//分割points字符串类型的点
void SplitString(const string& s, vector& v, const string& c)
{
	
	string::size_type pos1, pos2;
	pos2 = s.find(c);
	pos1 = 0;
	while (string::npos != pos2)
	{
		v.push_back(s.substr(pos1, pos2 - pos1));

		pos1 = pos2 + c.size();
		pos2 = s.find(c, pos1);
	}
	if (pos1 != s.length())
		v.push_back(s.substr(pos1));
}