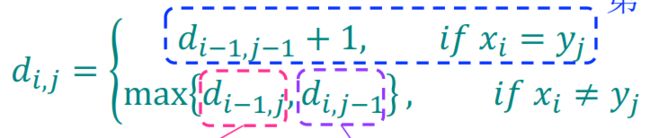动态规划——最长公共子序列问题

问题描述：

公共子序列：

动态规划求解步骤

Step 1: 分析最优解的性质，刻画其结构特征

Step 2: 递归地定义最优解

第一种情况：序列X的第i个元素与序列Y的第j个元素相等，则序列X、Y公共子序列长度=X、Y除去i,j位置元素后的

                     公共子序列长度+1

第二种情况：序列X的第i个元素与序列Y的第j个元素不相等，则公共子序列长度=序列X除去i位置元素与序列Y的最

                      长公共子序列  长度或序列Y除去j位置元素与序列X的最长公共子序列长度

Step 3: 自底向上计算子问题的最优解

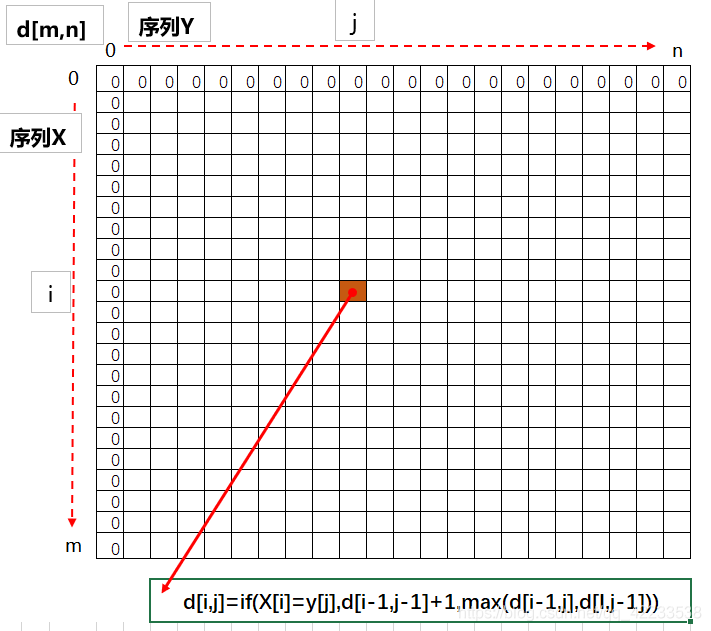
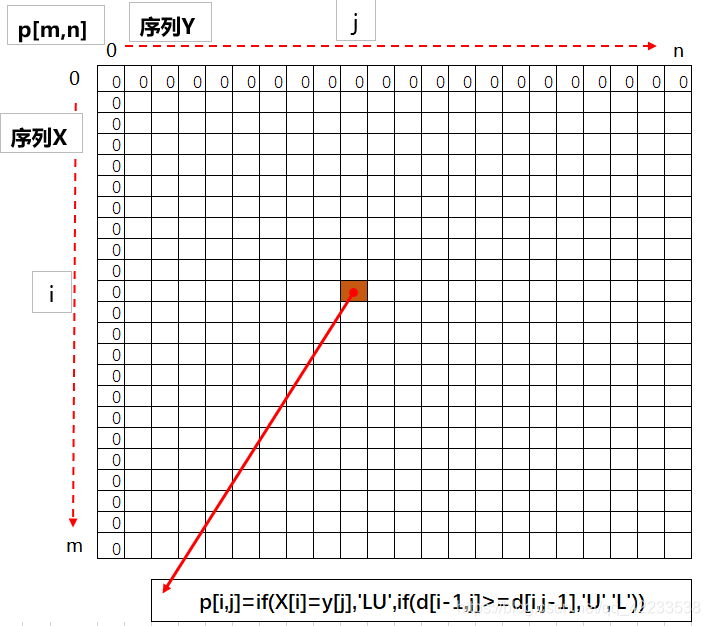
二维数组d[i,j]用来记录X[i]和Y[j]最长子序列长度	二维数组p[i,j]用来记录X[i]和Y[j]最长子序列的位置

Step 4: 构造问题的最优解 

伪代码解析

1.求解最长子序列

Longest-Common-Subsequence(X, Y)
输入：两个序列X,Y
输出：最长公共子序列
Input: Two strings , .
Output: Longest common subsequence of  and .
 ← length();  #序列X的长度为m
 ← length();   #序列Y的长度为n
步骤1：构建两个数组d[m,n],p[m,n](m行n列的二维数组)分别用来记录最长公共子序列的长度，
      公共子序列元素的位置
Let [0. . , 0. . ] and [0. . , 0. . ] be two new 2-dimension arrays;
步骤2：将二维数组d[m,n]的第一行，第一列置为0，即任何序列与空序列的最长公共子序列的长度均为0
for  ← 0   do
     [, 0] ← 0;
end
for  ← 0   do
     [0, ] ← 0;
end
步骤3:通过两层循环实现二维数组d[m,n]的所有元素的按行遍历，每一个单元格根据条件进行判断
for  ← 1   do
    for  ← 1   do
        if X[i]    Y[J] then
             [, ] ←  [ − 1,  − 1] + 1;
            [, ] ←”LU”;    //”LU” 表示矩阵左上角.
        end
        else if [ − 1, ] ≥ [,  − 1] then
             [,  ]←  [ − 1,  ];
            [, ] ←”U”;    //”U” 表示矩阵上边.
        end
        else
             [, ]←  [,  − 1] ;
            [, ] ←”L”;   //”L” 表示矩阵左边.
        end
       end
end
步骤4：返回二维数组d,p
return , ;

 2.输出最长子序列

#创建递归程序，实现程序遍历
Print-LCS(, X, , )
#输入  ：二维最长公共子序列数组 X:求解的序列 i,j分别为求解序列X[i],Y[j]的索引
Input: Array  generated from Longest-Common-Subsequence, string , index  and .
Output: Output the longest common subsequence of [1. . ] and [1. . ].
步骤1：如果索引i,j等于0，结束递归调用
if     0      0 then
    return NULL;
end
步骤2：如果 [, ]=“”，则表示X[i]=Y[j]，即上文中的第一种情况
if  [, ]    “” then
    Print-LCS(, ,  − 1,  − 1);
    print X[i];
end
如果 [, ]=“”，则最长子序列X[i,j]=X[i-1,j]，即上文中的第二种情况中第一种
else if  [, ]    “” then
    Print-LCS(, ,  − 1, );
end
如果 [, ]=“”，则最长子序列X[i,j]=X[i,j-1]，即上文中的第二种情况中第二种
else
    Print-LCS(, , ,  − 1);
end