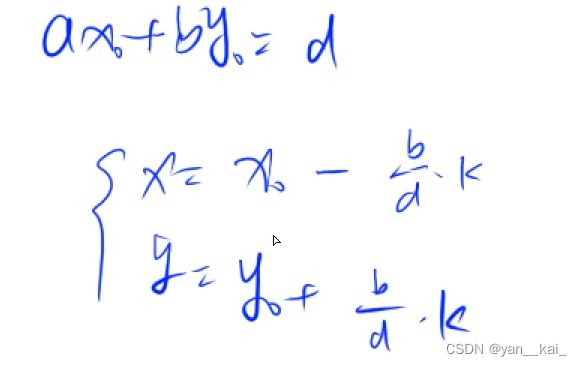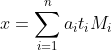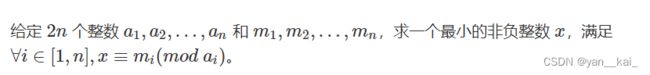第十一课:数学基础(快速幂、逆元、扩展欧几里得算法、中国剩余定理)
目录
〇、欧拉定理
一、快速幂
(1)定义及求法
(2)快速幂求逆元
二、扩展欧几里得算法
(1)推导和实现
(2)线性同余方程
三、中国剩余定理
(1)定理阐述
(2)样题:
〇、欧拉定理
若a与N互质,则a的phi(N)次方模N同余1。
若N是一个质数,则phi(N)=N-1:(费马小定理)
一、快速幂
(1)定义及求法
用途:快速求出a的k次方模p的值。
方式:1.预处理出a的2的x次方模p的值 的序列。其中x最大到log(k)。
则:
![]()
![]()
此时,发现k用二进制表示出来则可相应求得x的所有值。因此可以替换:
![]()
至于预处理这个序列,发现a的2的0次方a,a的2的一次方为a的平方。实际上后一项就是前一项的平方。因此预处理也比较方便。
eg:
快速幂的实际代码实现起来,融合了预处理与计算,需要牢记:
//这里填你的代码^^
#include
#include
using namespace std;
typedef long long LL;
LL qmi(int a,int b,int p)
{
//考虑b的二进制形式
LL res=1;
while(b)
{
if(b&1) res=res*a%p;//如果b该位有1
b>>=1;//去除一位
a=a*(LL)a%p;//a平方
}
return res;
}
int main()
{
int n;
cin>>n;
while(n--)
{
int a,b,p;
cin>>a>>b>>p;
cout< (2)快速幂求逆元
推导:
由费马小定理:
因此,x的一个可能解为:
b^p-2
求逆元,即用快速幂求出b的m-2次方模m的值。
代码:这里保证p是质数,因此可以用上述方法求解。如果不是质数,考虑扩展欧几里得算法。
//这里填你的代码^^
#include
#include
using namespace std;
typedef long long LL;
LL qmi(int a,int b,int p)
{
//考虑b的二进制形式
LL res=1;
while(b)
{
if(b&1) res=res*a%p;//如果b该位有1
b>>=1;//去除一位
a=a*(LL)a%p;//a平方
}
return res;
}
int main()
{
int n;
cin>>n;
while(n--)
{
int a,p;
cin>>a>>p;
int res=qmi(a,p-2,p);
if(a%p) cout< 二、扩展欧几里得算法
(1)推导和实现
扩展欧几里得算法:给定任意一对正整数a,b,求得一对整数x,y使得ax+by=gcd(a,b)。
推导:
回顾欧几里得算法,求最大公约数的边界时(即递归边界):
此时,对于(a‘,0),x,y的一组解为
考虑完了边界条件,在考虑一步步返回x,y的方式。对于(b,a mod b)的y,x,与(a,b)的x,y
从此可以看出,在一步步返回时,x不需要变动,而y需要按下式变化
拓展:实际上,x,y的解的结构为:
代码如下:
//这里填你的代码^^
#include
using namespace std;
int egcd(int a,int b,int& x,int& y)
{
if(!b)
{
x=1;
y=0;
return a;//如果b是0,a就是最大公约数,显然x=1,y=0是一组解
}
int d=egcd(b,a%b,y,x);//注意交换了y,x位置
//此时yb+x(a%b)=d。。所以对于a,b。(y-a/b*x)b+ax=d;对于a,b来说需要变换一下y
y -= a/b*x;
return d;
}
int main()
{
int n;
cin>>n;
while(n--)
{
int a,b,x,y;
cin>>a>>b;
egcd(a,b,x,y);
cout< (2)线性同余方程
给定a,b,m求出一个x,使得
。这样的方程称为线性同余方程。
解法推导:
![]()
![]()
由扩展欧几里得算法,我们可以求得k1,k2,使得:
![]()
因此,由裴蜀定理知,b一定是gcd(a,m)的倍数,若不是则方程无解。
若有解,易知:
代码:
//这里填你的代码^^
#include
using namespace std;
typedef long long LL;
int egcd(int a,int b,int& x,int& y)
{
if(!b)
{
x=1,y=0;
return a;
}
int d=egcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int main()
{
int n;
cin>>n;
while(n--)
{
int a,b,m;
cin>>a>>b>>m;
int x,y;
int d=egcd(a,m,x,y);
if(b%d) puts("impossible");
else cout<<(LL)x*b/d%m< 三、中国剩余定理
(1)定理阐述
中国剩余定理给定了以下的一元线性同余方程组:
中国剩余定理说明:假设整数m1,m2, ... ,mn两两互质,则对任意的整数:a1,a2, ... ,an,方程组![]() 有解,且通解可以用如下方式构造得到:
有解,且通解可以用如下方式构造得到:
则方程组通解为:
在模M的意义下,方程只有一个解:
原理简述:m之间两两互质,因此模mi时,下标同的mj mod mi ==0,而mi*mi的逆元模mi为1。
(2)样题:
解题推导:
首先选出方程组中两个方程:
则:
可以利用扩展欧几里得算法求得该式中的一组k1,k2。根据线性同余方程组解的结构,k1和k2的通解为:
可看成:
这样就将两个方程合并为了一个方程,如此把所有方程合并起来,求得最后方程形式为:
此时令k合理取值,使得x为方程能够达到的最小正整数即位题目所求。
细节注意:
1.用扩展欧几里得算法求解时,注意k1要扩大一个相应的倍数,有可能无解。
2.过程中需要不断累积的k1可能爆int,即需要![]() 方程需要控制k1为最小正整数解。
方程需要控制k1为最小正整数解。
代码如下:
//这里填你的代码^^
#include
#include
using namespace std;
typedef long long LL;
LL egcd(LL a,LL b,LL &x,LL &y)
{
if(!b)
{
x=1,y=0;
return a;
}
int d=egcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int main()
{
int n;
cin>>n;
LL a1,m1;
cin>>a1>>m1;
bool has_ans=true;
for(int i=0;i>a2>>m2;
LL k1,k2;
LL d=egcd(a1,a2,k1,k2);
if((m2-m1)%d)
{
has_ans=false;
break;
}
k1 *=(m2-m1)/d;//扩大倍数
LL t=a2/d;
k1=(k1%t+t)%t;//保留方程最小正整数解
m1=a1*k1+m1;//合并方程
a1=abs(a1/d*a2);
}
if(has_ans)
{
cout<<(m1%a1+a1)%a1;//保留方程最小正整数解
}
else cout<<"-1";
return 0;
}
//注意代码要放在两组三个点之间,才可以正确显示代码高亮哦~
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/3763166/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。