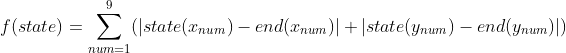搜索（2）bfs扩展

 

目录

一、双端队列广搜 

二、双向广搜

三、A*算法

1.概述

2.八数码 A*算法 

3.第k短路

---

 

一、双端队列广搜 

 从起点bfs找最短路到终点。在遍历过程中，我们到一个新的点时，发现如果电路板上得到原有的线段能够让我们到这个新的点，则这个新的点的dist不变。如果不能，需要旋转，新的点dist要+1。为了维护bfs队列中的两段性和单调性，我们应该把dist不变的放到队头，dist+1的放到队尾，这样就能保证bfs的正确性。

细节：dist是表示的是电路板上的点，，g数组存的是电路板上的格子。因此用ix表示了某个点四个方向上的边在g数组中的位置。

#include
#include
#include
#include
#define x first
#define y second
using namespace std;

typedef pair PII;

const int N =510;

int n,m;
char g[N][N];
int dist[N][N];
bool st[N][N];


int bfs()
{
    memset(dist,0x3f,sizeof dist);
    memset(st,0,sizeof st);

    dist[0][0]=0;
    deque q;
    q.push_back({0,0});

    char cs[] = "\\/\\/";//   =="\/\/"
    int dx[4]={-1,-1,1,1},dy[4]={-1,1,1,-1};
    int ix[4]={-1,-1,0,0},iy[4]={-1,0,0,-1};  //这个点四个方向的边 在g数组中的下标

    while(q.size())
    {
        auto t=q.front();
        q.pop_front();

        if(st[t.x][t.y])  continue;

        st[t.x][t.y]=true;

        for(int i=0;i<4;i++)
        {
            int a=t.x+dx[i],b=t.y+dy[i];
            if(a<0||b<0||a>n||b>m) continue;

            int ca=t.x+ix[i],cb=t.y+iy[i];
            int d=dist[t.x][t.y]+(g[ca][cb]!=cs[i]);

            if(d>T;
    while(T--)
    {
        cin>>n>>m;

        for(int i=0;i>g[i];

        if(n+m&1)
        {
            puts("NO SOLUTION");
            continue;
        }

        cout<

二、双向广搜

 设每次搜索的决策数量是K，如果正常直接bfs，则最终搜索树的规模是K^10，规模非常大。但是如果从起点和终点同时向目标态搜索，规模数量能降为2*K^5，效果非常明显。BFS的扩展方式是：分别枚举在原字符串中使用替换规则的起点，和所使用的的替换规则。

假设字符串长度是 L，替换规则一共有 N 个，则：

在最坏情况下每次会从字符串的每个位置开始，使用全部的 N 种替换规则，因此总共会有 L*N 种扩展方式，从起点和终点最多会分别扩展5步，因此总搜索空间是 2(LN)^5。

在BFS过程中，空间中的每个状态只会被遍历一次，因此时间复杂度是 O((LN)^5)。

细节：1.

 2.每次从搜索量较小的一层搜起

3.代码略长，记住具体代码实现方式。

#include
#include
#include
#include
#include
using namespace std;

const int N =6;

int n;
string A,B;
string a[N],b[N];

int extend(queue& q, unordered_map&da, unordered_map& db, 
    string a[N], string b[N])
{
    int d=da[q.front()];
    while(q.size()&&da[q.front()]==d)//扩展一层，之前的不扩展
    {
        auto t=q.front();
        q.pop();
        for(int i=0;i qa,qb;
    unordered_map da,db;
    qa.push(A),qb.push(B);
    da[A]=da[B]=0;
    int step=0;

    while(qa.size()&&qb.size())
    {
        int t;
        if(qa.size()b
        else t=extend(qb,db,da,b,a);

        if(t<=10) return t;
        if(++step==10) return -1;
    }
    return -1;
}



int main()
{
    cin>>A>>B;
    while(cin>>a[n]>>b[n]) n++;

    int t=bfs();
    if(t==-1) puts("NO ANSWER!");
    else cout<

三、A*算法

1.概述

回顾优先队列bfs算法，该算法维护了一个二叉堆，每次取出当前代价最小的状态进行扩展。每次状态第一次从堆中取出时，就得到了初态到该状态的最小代价。

如果给定一个目标状态，需要求初态到目标状态的最小代价，那么优先队列bfs显然不完善。因为一个状态的当前代价最小，而在未来的搜索中，该状态可能到目标状态的代价很大。优先队列bfs可能会选择当前代价较小而未来代价很大的状态先扩展，导致求出最优解的搜索量最大。

为了提高搜索效率，我们自然想到，可以设计一个“估价函数”，计算出从该状态到目标状态所需代价的估计值。在搜索中，仍然维护一个堆，不断从堆中取出“当前代价+未来估价”最小的状态进行扩展。

为了保证第一次从堆中取出目标状态时得到的就是最优解，我们设计的估价函数需要满足：对任意状态state，都有估计值f(state)<=真实值g(state)。

即估价函数不能大于未来实际代价。

原因：在搜索时，有可能某些状态被错误估计了较大的代价，被压在堆中无法取出，从而导致非最优解搜索路径上的状态不断被扩展，直至在目标状态上产生了错误的答案。如果加上估价函数不大于未来实际代价的限制，那么即是估价不太准确，导致非最优解搜索路径上的s先被扩展，但是随着“当前代价”不断累加，在目标状态被取出前的某个时刻，一定有：

1.因为s并非最优解，s的“当前代价”就会大于从起始状态到目标状态的最小代价。

2.对于最优解搜索路径上的t，因为f(t)<=g(t)，所以t的当前代价加上f(t)后必定小于“当前代价”+g(t),即最优解。

那么此时t就会被从堆中取出进行扩展，回到最优解搜索路径上，最终到达目标状态，得到最优解。

这种带有估价函数的优先队列bfs就被称为A*算法。只要保证对于任意状态，估价函数小于等于实际代价，A*算法就一定能在目标状态第一次被取出时得到最优解。估价越准确，效率就留越高。

2.八数码 A*算法 

 本题当然可以直接bfs，做法在最先发布的bfs中介绍过。

本题可以考虑设计估价函数，来加快搜索效率。一般设计估价函数，可以假设每一次都能最理想的靠近目标状态，求出的理想值可以作为估价值（满足一定小于实际价值）

先进行可行解判定，一个常用技巧：把除空格之外的所有数字排成一个序列，求出该序列的逆序对数。如果初态和终态的逆序对数奇偶性相同，那么这两个状态可互相到达，否则一定不可达。

必要性证明：奇数码游戏中，空格左右移动时，写出的序列不变。空格上下移动时，即某个数i与他后边的n-1个数j交换。对这n-1中的任意一个数k。如果k>i,k>j，则交换之后逆序对数量不变；k>i,k

接下来设计估价函数：每一次只能把一个数字和空格交换位置。这样至多把一个数字向目标状态接近一步。假设每一步移动都是有意义的，从任何一个状态到目标状态的移动步数不可能小于所有数字当前位置与目标位置的曼哈顿距离之和。

于是，对于任意状态state，估价函数有：

注意A*算法中每个状态可能不止被拓展一次，因此判断状态转移的条件为 ：

因为可能state状态在错误的路径上被拓展到了，然后被赋了一个较大的值。现在走到了最优解路径上，state的仍需要被更新并加入队列中扩展。 

#include
#include
#include
#include
#include
#define x first
#define y second

using namespace std;

typedef pair PIS; //当前+估价值  当前状态


int f(string state)
{
    int res = 0;
    for (int i = 0; i < state.size(); i ++ )
        if (state[i] != 'x')
        {
            int t = state[i] - '1';
            res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3);
        }
    return res;
}

string bfs(string start)
{
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    char op[4] = {'u', 'r', 'd', 'l'};

    string end="12345678x";
    unordered_map dist;
    unordered_map> prev;
    priority_queue,greater > heap;   

    heap.push({f(start),start});
    dist[start]=0;

    while(heap.size())
    {
        auto t=heap.top();
        heap.pop();

        string state =t.y;
        if(state==end) break;

        int x,y;
        for(int i=0;i=0 && a<3 && b>=0 && b<3)
            {
                swap(state[x*3+y],state[a*3+b]);
                if(!dist.count(state)||dist[state]>dist[source]+1)
                {
                    dist[state]=dist[source]+1;
                    prev[state]={source,op[i]};
                    heap.push({dist[state]+f(state),state});
                }
                swap(state[x*3+y],state[a*3+b]);
            }
        }

    }


    string res;
    while(end!=start)
    {
        res+=prev[end].y;
        end=prev[end].x;
    }
    reverse(res.begin(),res.end());
    return res;
}

int main()
{
    string start, c, seq;
    while (cin >> c)
    {
        start += c;
        if (c != "x") seq += c;
    }   

    int t=0;
    for(int i=0;iseq[j])
                t++;
    if(t%2) puts("unsolvable") ;
    else cout<

3.第k短路

 找第k短路，需要遍历所有路径：即遍历到节点i时，不需判断地把所有邻点加入优先队列中。（保证能够枚举到所有路径）， 显然，这样的话整个搜索空间非常庞大。因此考虑A*算法

 由上面的介绍，本题自然想到估价函数可以设计为：节点i到终点的最短路径长度。

显然最短路径长度一定小于第k短路长度，因此估价函数是可用的。

证明终点第一次出队列即最优解

    1 假设终点第一次出队列时不是最优 
      则说明当前队列中存在点u
         有 d[估计]< d[真实]
      d[u] + f[u] <= d[u] + g[u] = d[队头终点]
      即队列中存在比d[终点]小的值,
    2 但我们维护的是一个小根堆,没有比d[队头终点]小的d[u],矛盾

由数学归纳法，，终点第k次出队即为第k短路值。

算法流程：

1. 反向建图跑dijkstra，得终点到各个点的最短路径
2. 建立优先队列，存储{x，dist+f(x)}，起初只有{0，0+f(0)}
3. 跑类似bfs，遍历图。每次取出堆顶元素，把其所有邻点加入堆中
4. 第k次取出终点时即为答案。
5. 特别地，每条最短路中至少包含一条边，所以当 S == T 的时候，需要让 K ++。

#include
#include
#include
#include
#define x first 
#define y second
using namespace std;

typedef pair PII;
typedef pair> PIII;

const int N =1010,M=200010;
int n,m,S,T,K;
int h[N],rh[N],e[M],ne[M],w[M],idx;
int dist[N];
bool st[N];


void add(int h[],int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

//预处理  反向图求终点到各节点的距离
void dijkstra()
{
    priority_queue,greater > heap;
    heap.push({0,T});

    memset(dist,0x3f,sizeof dist);
    dist[T]=0;

    while(heap.size())
    {
        auto t=heap.top();
        heap.pop();

        int ver=t.y;
        if(st[ver]) continue;

        st[ver]=true;
        for(int i=rh[ver];~i;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[ver]+w[i])
            {
                dist[j]=dist[ver]+w[i];
                heap.push({dist[j],j});
            }
        }
    }
}


int astar()
{
    if(dist[S]==0x3f3f3f3f) return -1;
    priority_queue,greater > heap;//估价值 {真实值，编号}
    heap.push({dist[S],{0,S}});

    int cnt=0;
    while(heap.size())
    {
        auto t=heap.top();
        heap.pop();

        int ver=t.y.y,distance=t.y.x;
        if(ver==T) cnt++;
        if(cnt==K) return distance;

        for(int i=h[ver];~i;i=ne[i])
        {
            int j=e[i];
            heap.push({dist[j]+distance+w[i],{distance+w[i],j}}); //把所有相连的结点扩展进队列
        }
    }
    return -1;
}

int main()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);
    memset(rh,-1,sizeof rh);

    for(int i=0;i>a>>b>>c;
        add(h,a,b,c);
        add(rh,b,a,c);
    }
    //每条最短路中至少包含一条边，所以当 S == T 的时候，需要让 K ++。
    cin>>S>>T>>K;
    if(S==T) K++;

    dijkstra();
    cout<