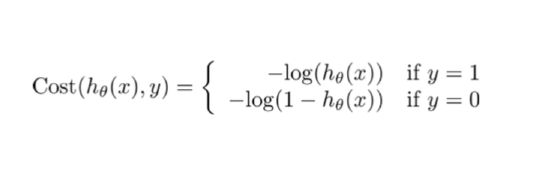机器学习-逻辑斯蒂回归(Logistic Regression)
注:内容转自https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning,略有修改。
目录
逻辑
1. 什么是逻辑斯蒂回归
2. 什么是Sigmoid函数
3. 损失函数是什么
4.可以进行多分类吗?
5.逻辑斯蒂回归有什么优缺点
6. 逻辑斯蒂回归有哪些应用
7. 逻辑斯蒂回归常用的优化方法有哪些
7.1 一阶方法
7.2 二阶方法:牛顿法、拟牛顿法:
8. 逻辑斯特回归为什么要对特征进行离散化。
9. 逻辑回归的目标函数中增大L1正则化会是什么结果。
10. 代码实现
逻辑
1. 什么是逻辑斯蒂回归
逻辑回归是用来做分类算法的,大家都熟悉线性回归,一般形式是Y=aX+b,y的取值范围是[-∞, +∞],有这么多取值,怎么进行分类呢?不用担心,伟大的数学家已经为我们找到了一个方法。
也就是把Y的结果带入一个非线性变换的Sigmoid函数中,即可得到[0,1]之间取值范围的数S,S可以把它看成是一个概率值,如果我们设置概率阈值为0.5,那么S大于0.5可以看成是正样本,小于0.5看成是负样本,就可以进行分类了。
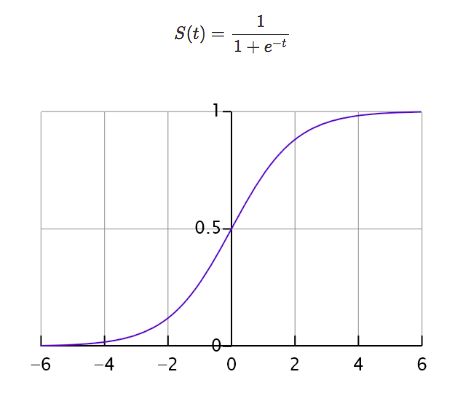
2. 什么是Sigmoid函数
函数公式如下:
函数中t无论取什么值,其结果都在[0,1]的区间内,回想一下,一个分类问题就有两种答案,一种是“是”,一种是“否”,那0对应着“否”,1对应着“是”,那又有人问了,你这不是[0,1]的区间吗,怎么会只有0和1呢?这个问题问得好,我们假设分类的阈值是0.5,那么超过0.5的归为1分类,低于0.5的归为0分类,阈值是可以自己设定的。
好了,接下来我们把aX+b带入t中就得到了我们的逻辑回归的一般模型方程:
结果P也可以理解为概率,换句话说概率大于0.5的属于1分类,概率小于0.5的属于0分类,这就达到了分类的目的。
3. 损失函数是什么
二项逻辑回归的条件概率分布为:
![]()
![]()
因此,其似然函数为:
求模型参数\theta, 也就是使得似然函数为最大值时对应的参数\theta, 对似然函数取对数,也就是要求对数似然函数取最大值:
由于损失函数一般是取最小值,因此损失函数定义为对数似然函数的相反数,即
化成分段函数公式如下:
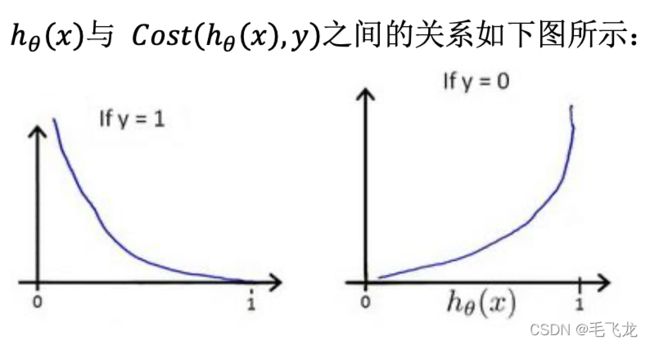
这样构建的(h(),)函数的特点是:
- 当实际的 = 1 且h()也为 1 时误差为 0, 当 = 1 但h()不为 1 时误差随着h()变小而变大;
- 当实际的 = 0 且h()也为 0 时 代价为 0,当 = 0 但h()不为 0 时误差随着 h()的变大而变大
最后按照梯度下降法一样,求解极小值点,得到想要的模型效果。
4.可以进行多分类吗?
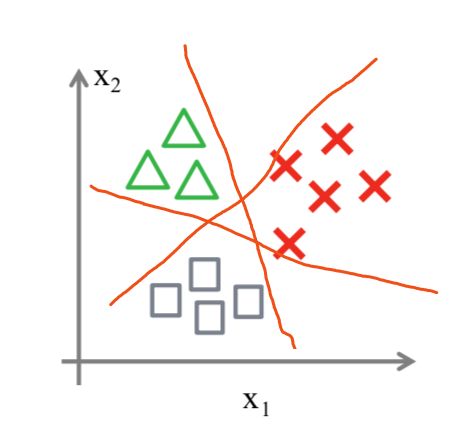
可以的,其实我们可以从二分类问题过度到多分类问题(one vs rest),思路步骤如下:
1.将类型class1看作正样本,其他类型全部看作负样本,然后我们就可以得到样本标记类型为该类型的概率p1。
2.然后再将另外类型class2看作正样本,其他类型全部看作负样本,同理得到p2。
3.以此循环,我们可以得到该待预测样本的标记类型分别为类型class i时的概率pi,最后我们取pi中最大的那个概率对应的样本标记类型作为我们的待预测样本类型。
总之还是以二分类来依次划分,并求出最大概率结果。
5.逻辑斯蒂回归有什么优缺点
优点
- LR能以概率的形式输出结果,而非只是0,1判定。
- LR的可解释性强,可控度高(你要给老板讲的嘛…)。
- 训练快,feature engineering之后效果赞。
- 因为结果是概率,可以做ranking model
缺点
- 不能用Logistic回归去解决非线性问题,因为Logistic的决策面试线性的;
- 对多重共线性数据较为敏感;
- 很难处理数据不平衡的问题;
- 准确率并不是很高,因为形式非常的简单(非常类似线性模型),很难去拟合数据的真实分布
- 逻辑回归本身无法筛选特征,有时会用gbdt来筛选特征,然后再上逻辑回归
6. 逻辑斯蒂回归有哪些应用
- CTR预估/推荐系统的learning to rank/各种分类场景。
- 某搜索引擎厂的广告CTR预估基线版是LR。
- 某电商搜索排序/广告CTR预估基线版是LR。
- 某电商的购物搭配推荐用了大量LR。
- 某现在一天广告赚1000w+的新闻app排序基线是LR。
7. 逻辑斯蒂回归常用的优化方法有哪些
7.1 一阶方法
梯度下降、随机梯度下降、mini 随机梯度下降降法。随机梯度下降不但速度上比原始梯度下降要快,局部最优化问题时可以一定程度上抑制局部最优解的发生。
7.2 二阶方法:牛顿法、拟牛顿法:
这里详细说一下牛顿法的基本原理和牛顿法的应用方式。牛顿法其实就是通过切线与x轴的交点不断更新切线的位置,直到达到曲线与x轴的交点得到方程解。在实际应用中我们因为常常要求解凸优化问题,也就是要求解函数一阶导数为0的位置,而牛顿法恰好可以给这种问题提供解决方法。实际应用中牛顿法首先选择一个点作为起始点,并进行一次二阶泰勒展开得到导数为0的点进行一个更新,直到达到要求,这时牛顿法也就成了二阶求解问题,比一阶方法更快。我们常常看到的x通常为一个多维向量,这也就引出了Hessian矩阵的概念(就是x的二阶导数矩阵)。
缺点:牛顿法是定长迭代,没有步长因子,所以不能保证函数值稳定的下降,严重时甚至会失败。还有就是牛顿法要求函数一定是二阶可导的。而且计算Hessian矩阵的逆复杂度很大。
拟牛顿法: 不用二阶偏导而是构造出Hessian矩阵的近似正定对称矩阵的方法称为拟牛顿法。拟牛顿法的思路就是用一个特别的表达形式来模拟Hessian矩阵或者是他的逆使得表达式满足拟牛顿条件。主要有DFP法(逼近Hession的逆)、BFGS(直接逼近Hession矩阵)、 L-BFGS(可以减少BFGS所需的存储空间)。
8. 逻辑斯特回归为什么要对特征进行离散化。
- 非线性!非线性!非线性!逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合; 离散特征的增加和减少都很容易,易于模型的快速迭代;
- 速度快!速度快!速度快!稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
- 鲁棒性!鲁棒性!鲁棒性!离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
- 方便交叉与特征组合:离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
- 稳定性:特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问;
- 简化模型:特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险。
9. 逻辑回归的目标函数中增大L1正则化会是什么结果。
所有的参数w都会变成0。
10. 代码实现
https://nbviewer.org/github/maofeilong/100-Days-Of-ML-Code-1/blob/c5e8bcea740355d7f9b48cbcf4f9237108d7e408/Day%206_Logistic_Regression.ipynb![]() https://nbviewer.org/github/maofeilong/100-Days-Of-ML-Code-1/blob/c5e8bcea740355d7f9b48cbcf4f9237108d7e408/Day%206_Logistic_Regression.ipynb
https://nbviewer.org/github/maofeilong/100-Days-Of-ML-Code-1/blob/c5e8bcea740355d7f9b48cbcf4f9237108d7e408/Day%206_Logistic_Regression.ipynb
参考:在此基础上略有更改
https://github.com/MLEveryday/100-Days-Of-ML-Code/edit/master/Code/Day%206_Logistic_Regression.md
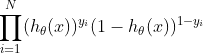
![L(\theta) = \sum_{i=1}^{N} [{y_{i}} (h_{\theta}(x)) + ({1-y_{i}})(1-h_{\theta}(x))]](http://img.e-com-net.com/image/info8/bb7f86e8903445e494c1eb5818690e35.gif)
![Cost(h_{\theta}(x),y) = -L(\theta) = -\sum_{i=1}^{N}[{y_{i}} (h_{\theta}(x)) + ({1-y_{i}})(1-h_{\theta}(x))]](http://img.e-com-net.com/image/info8/7999ffca2d80402baa32130506751bdb.gif)