数据结构--4.2 哈夫曼树
哈夫曼树
- 哈夫曼树
-
- 哈夫曼树的定义
- 哈夫曼树的伪算法
- 代码实现
-
- 寻找最小的两个权重
- 构造哈夫曼树
- 运行结果
- 总代码
哈夫曼树
哈夫曼树的定义
今天敲得是一类很特别的树–哈夫曼树。
设有n个权值{w1,w2,w3,…,wn},构造有n个叶子结点的二叉树,每个叶子结点带权为wi,则其中带权路径长度最小的二叉树称为哈夫曼树或最优二叉树。
这里要注意几点,带权路径长度最小可以构成的哈夫曼树不止一个;n个权值构造的哈夫曼树的节点有2*n-1个。
哈夫曼树的伪算法
哈夫曼树的伪算法可以用一句话总结:
依次选择权值最小的二个结点作为左右子树构造一颗新的二叉树,其产生的根结点的权值为左右子树权值之和。一直重复直到只含一棵树为止。
这句话可以展开成下面四个步骤:
(1)根据给定的n个权值{w1,w2,w3,…,wn}构成n棵二叉树的集合(森林),其中每棵二叉树Ti中只有一个带权为wi的根结点,其左右子树均为空。

(2)在森林中选取两棵根结点权值最小的树作为左右子树构造一棵新的二叉树,新二叉树的根结点的权值为其左右子树上根结点的权值之和.

(3)在集合F中删除这两棵树,同时将新得到的二叉树加入森林中.
(4)重复步骤(2)、(3),直到F中只含一棵树为止,这棵树就是一棵赫夫曼树.
最终我们可以得到如下结果:
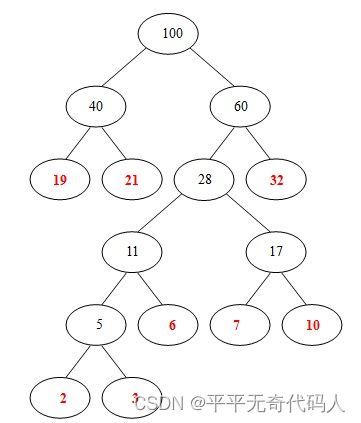
代码实现
寻找最小的两个权重
void select_Tree(HuffmanTree HT,int n,int &s1,int &s2)
{
int min;
int i;
printf("select\r\n");
//找第一个最小值
for(i = 1;i <= n;i++)
{
if(HT[i].parent == 0)
{
min = i;
break;
}
}
for(i = min+1;i <= n;i++)
{
if(HT[i].parent == 0&&HT[i].weight < HT[min].weight )
{
min = i;
}
}
s1 = min;
printf("s1 = %d\n",s1);
//找第二个最小值
for(i = 1;i <= n;i++)
{
if(HT[i].parent == 0&&i != s1)
{
min = i;
break;
}
}
for(i = min+1;i <= n;i++)
{
if(HT[i].parent == 0 && HT[i].weight <= HT[min].weight && min != s1)
{
min = i;
}
}
s2 = min;
printf("s2 = %d\n",s2);
}
构造哈夫曼树
void creat_Tree(HuffmanTree HT,int n)
{
int m,i;
int s1,s2;
printf("creat\r\n");
if(n <= 1)
{
return;
}
m = 2*n - 1;//数组一共有2n-1个元素;
HT = (HuffmanTree)calloc(m+1,sizeof(Huffman));
for(i = 1;i <= m ;i++)
{
HT[i].lch = 0;
HT[i].rch = 0;
HT[i].parent = 0;
}
printf("in weight\n");
for(i = 1;i<=n;i++)
{
std::cin>>HT[i].weight ;
}//输入权重
printf("111\r\n");
for(i = n+1;i <= m;i++)//合并产生n-1个节点-构造哈夫曼树
{
select_Tree(HT,i-1,s1,s2);//在ht[k](1<=k<=i-1),找最小且双亲域为0的两个节点,返回它们在ht中的序号
HT[i].weight = HT[s1].weight + HT[s2].weight ;//i的权值为s1和s2之和
HT[s1].parent = i;
HT[s2].parent = i;//从ht中删除s1和s2
HT[i].lch = s1;
HT[i].rch = s2;
printf("HT[%d].weight = %d,HT[%d].weight = %d\r\n",s1,HT[s1].weight,s2,HT[s2].weight );
printf("end of %d\r\n HT[%d].weight = %d\r\n",i,i,HT[i].weight );
}
printf("哈夫曼树为:>\n");
printf("下标 权值 父结点 左孩子 右孩子\n");
printf("0 \n");
for (int i = 1; i <= m; i++)
{
printf("%-4d %-6d %-6d %-6d %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lch, HT[i].rch);
}
printf("\n");
}
运行结果
请输入数据个数:
3
creat
in weight
3
2
1
111
select
s1 = 3
s2 = 3
HT[3].weight = 1,HT[3].weight = 1
end of 4
HT[4].weight = 2
select
s1 = 2
s2 = 2
HT[2].weight = 2,HT[2].weight = 2
end of 5
HT[5].weight = 4
哈夫曼树为:>
下标 权值 父结点 左孩子 右孩子
0
1 3 0 0 0
2 2 5 0 0
3 1 4 0 0
4 2 0 3 3
5 4 0 2 2
总代码
#include