【R语言】典型相关分析，自写函数计算相关系数

简单相关系数

简单相关系数的代码实现
1.XY都是随机变量，地位对称
2.相关系数只反映两变量之间线性相关的程度，不能说明其非线性相关关系。
3.虽能度量相关关系，但是不能度量变量间的因果关系
公式

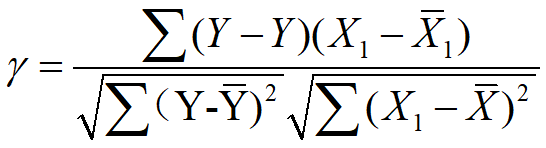
library('charlatan') # 造假数据的包
# 创建10个名
name = ch_name(10)

# 创建10个均分分布的数据 看看直方图
# 产生数据
set.seed(1) # 保持每次产生数据已知
x1 = ch_unif(10)
hist(x1,breaks = 4)
x2 = ch_unif(10)/200
hist(x2,breaks = 4)
y = 0.5*x1+0.14*x2+rnorm(1) # 加噪声


# 法1
# 计算相关系数
fun_rxy = function(x,y){
  x_bar = mean(x)
  y_bar = mean(y)
  print(x_bar)
  print(y_bar)
  fenzi = sum((x-x_bar)*(y-y_bar))
  print(fenzi)
  fenmu = sqrt(sum((x-x_bar)^2)*sum((y-y_bar)^2))
  print(fenmu)
  r_xy = fenzi/fenmu
  print('相关系数为：')
  print(r_xy)
}
fun_rxy(x1,y)

# 法2
## pearson系数
pearson<-function(x,y){
  xp<-sum(x)/length(x)
  yp<-sum(y)/length(y)
  f1 = f2 = f3 = 0
  for (i in 1:length(x)){
    f1 = f1 + (x[i]-xp)*(y[i]-yp)
    f2 = f2 + (x[i]-xp)^2
    f3 = f3 + (y[i]-yp)^2
  }
  cor = f1/(sqrt(f2)*sqrt(f3))
  
  return(cor)
}
pearson(x1,y)


cor(x1,y,method = "pearson")

偏相关系数

  设x1 ，x2，y是三个变量，如果要计算x2给定的条件下， x1 和y的相关系数，应该用偏相关系数更合理，那么偏相关系数为： 

公式：

#-------------偏相关系数
#R语言包里面有 偏相关系数
library(ggm)
df = data.frame(x1,x2,y)
jsbl = c(1,3) # x1,y计算相关系数
kzbl = c(2) # x2下标是控制变量
con = c(jsbl,kzbl)
c1 = cov(df) # 协方差

pcor1 = function (u, S) 
{
  k <- solve(S[u, u],tol=2e-21)
  k[1, 2]/sqrt(k[1, 1] * k[2, 2])
}
pcor1(con,c1) # 偏相关

# 法2
r_yx1x2 = (cor(x1,y)-cor(x2,y)*cor(x1,x2))/(sqrt(1-cor(x2,y)^2)*sqrt(1-cor(x1,x2)^2))
r_yx1x2

spearman相关系数

在给定一列数对（x1,y1），····，（xn,yn）之后，要检验他们所代表的二元变量X和Y是否相关。首先将X和Y的观测值分别排序，分别得各自得秩统计量，Spearman相关检验的含义是直接对秩统计量计算相关系数，即计算R和S的相关系数 ：
公式：

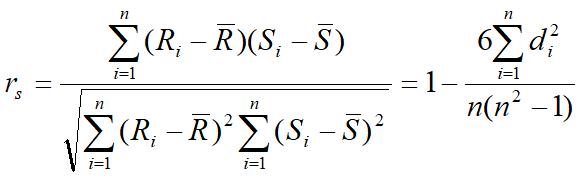
其中：

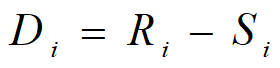
#------------spearman----
# 法1
##  spearman系数
cor(x,y,method = "spearman")
spearman<-function(x,y){
  u<-rank(x)
  v<-rank(y)
  up<-sum(u)/length(u)
  vp<-sum(v)/length(v)
  f1 = f2 = f3 = 0
  for (i in 1:length(u)){
    f1 = f1 + (u[i]-up)*(v[i]-vp)
    f2 = f2 + (u[i]-up)^2
    f3 = f3 + (v[i]-vp)^2
  }
  cor = f1/(sqrt(f2)*sqrt(f3))
  
  return(cor)
}
spearman(x1,y)


#法2
##  spearman系数
f1 = 0
cor(x1,y,method = "spearman")
spearman<-function(x,y){
  n<-length(x)
  u<-rank(x)
  v<-rank(y)
  f1 = f2 = f3 = 0
  for (i in 1:n){
    f1 = f1 + (u[i]-v[i])^2
  }
  cor = 1-6*f1/(n*(n^2-1))
  
  return(cor)
}
spearman(x1,y)

复相关系数

      简单相关系数和偏相关系数实际上均是讨论两个变量的关系，但常常我们会讨论一个变量和一组变量的相关，这叫复相关系数。实际上一个变量和一组变量的复相关是以这个变量为被解释变量，以这组变量为回归因子，建立回归模型的可决系数R2. 

总体典型相关

我用内置的检验，老是发现不对，也不知道错在哪里！

#--------------典型相关系数和典型变量求解
## 定义函数,求两个矩阵的典型变量和典型相关系数
My.rtest = function(x,y){
  # 计算相关系数矩阵
  R11 = cov(x)
  R12 = cov(x,y)
  R21 = cov(y,x)
  R22 = cov(y)
  
  M1 = solve(R11)%*%R12%*%solve(R22)%*%R21
  M2 = solve(R22)%*%R21%*%solve(R11)%*%R12
  
  #使用函数eigen()计算特征值和特征向量
  ev1 = eigen(M1) 
  ev2 = eigen(M2) 
  
  lamda0 = ev1$val #访问列表values项，即特征值
  lamda = sqrt(lamda0) #典型相关系数
  
  #a_k = solve(R11)^(0.5)%*%ev1$val
  #b_k = (1/lamda[1])*solve(R22)^(0.5)%*%R21%*%lamda
  alpha = ev1$vec #访问列表vectros项，即特征向量
  beta = ev2$vec #访问列表vectros项，即特征向量
  
  #求典型变量u和v的系数
  u = t(alpha) #第k行即第k个典型变量的系数
  v = t(beta) #第k行即第k个典型变量的系数
  #print(a_k)
  #u = t(a_k)%*%x
  #v = t(b_k)%*%y
  
  
  result = list(lamda=lamda,u=u,v=v)
  print(result)
}

#随机产生数据矩阵
#x1 = matrix(runif(10,0,5),10)
#x2 = matrix(runif(10,0,10),10)
#x = cbind(x1,x2)

#y1 = matrix(runif(10,-2,5),10)
#y2 = matrix(runif(10,3,6),10)
#y3 = matrix(runif(10,-10,6),10)
#y =cbind(y1,y2,y3)

x1=c(191, 193, 189, 211, 176, 169, 154, 193, 176, 156, 189, 162, 182, 167, 154, 166, 247, 202, 157, 138)
x2=c(36, 38, 35, 38, 31, 34, 34, 36, 37, 33, 37, 35, 36, 34, 33, 33, 46, 37, 32, 33)
x3=c(50, 58, 46, 56, 74, 50, 64, 46, 54, 54, 52, 62, 56, 60, 56, 52, 50, 62, 52, 68)
x = scale(cbind(x1,x2,x3))
y1=c( 5, 12, 13,  8, 15, 17, 14,  6,  4, 15, 2, 12,  4,  6, 17, 13,  1, 12, 11,  2)
y2=c(162, 101, 155, 101, 200, 120, 215,  70,  60, 225, 110, 105, 101, 125, 251, 210,  50, 210, 230, 110)
y3=c(60, 101, 58, 38, 40, 38, 105, 31, 25, 73, 60, 37, 42, 40, 250, 115, 50, 120, 80, 43)
y = scale(cbind(y1,y2,y3))


#调用该函数
My.rtest(x,y)

# R语言内置检验
ca = cancor(x,y)
ca