论文阅读笔记 之 3D Bounding Box Estimation Using Deep Learning and Geometry

发表时间及期刊/会议 : 2017 CVPR
论文地址：https://arxiv.org/abs/1612.00496

一、 解决的主要问题

单目图像实现3D目标检测

已有条件/输入： 相机的内参矩阵K, 单目相机图像

需要求的结果：3D bounding box 的中心，尺寸，方向，即：
 中心坐标： t_x, t_y, t_z,
 尺寸： d_x, d_y, d_z,
 方向： 偏转角θ，（Φ, α ：默认目标翻滚角与俯仰角为0）

二、 预备知识

对于相机坐标系中的任一目标，都可以通过旋转平移矩阵[R T]将该目标的目标坐标系转为相机坐标系, 即对于目标上的任意一点X_0，都可以通过乘以[R T]将该点的目标坐标系中的坐标转为在相机坐标系中的坐标。同时因为相机内参矩阵K已知，内参矩阵可以将相机坐标系坐标转为图像坐标系中的坐标。因此可以得到某一点在2D图像坐标系与目标坐标系中坐标的关系：

其中x = [x,y,1]为该点的图像齐次坐标，X_0 = [X,Y,Z,1]为该点在目标坐标系中的齐次坐标。

三、 论文内容：

  现需要根据图像坐标以及相机内存矩阵反推X_0以及[R T]，因为[R T]包含了目标的方向、中心坐标信息（都是相对于相机坐标系）
可以看出由于维度不同，并不能直接通过解方程组计算结果。因此需要选取几个参数利用神经网络对其进行估计。本论文作者使用神经网络来估计目标的尺寸d_x, d_y, d_z 以及 方向即偏转角θ。
  因为3D bounding box的方差较小，并且与目标的类别信息密切相关，能够利用类别信息精确化尺寸。
至此坐标转换方程
中仅剩下平移矩阵T中的3个参数未知，文章中并没有利用3D box的中心与2D box的中心对应（很多文章认为两者的中心是对应的）来计算，而是通过3D box的各个角点与2D bo的几何约束来计算。
  论文中认为 2D边框的每一条边必然至少与3D边框的一个角点接触，并且在默认翻滚角与俯仰角均为0的情况下3D 边框的竖直的边一定是与2D框的竖直边框重合的，如下图所示

红框为2D检测框，黑色坐标系为目标坐标系，以右上角的角点为例可以得到：

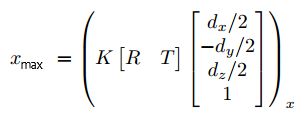
其中 (.)X 表示坐标的x维度的值，d_x, d_y, d_z分别为估计的3D边框的尺寸。同理可以得到关于x_max, y_min, y_max的方程，共4个方程，解该方程组即可得到剩下的3个未知量

（疑问：这就变成4个方程求解3个未知量了，维度反而多了一个，会不会出现冲突解，或者说是有一个多余的方程？）

（疑问：方程最后的角点选取是根据估计的偏转角来确定的？例如偏转角分别为45°、90°、135°时右上角的角点不是同一个角点，即在目标坐标系中的坐标也不同）

四、 CNN估计3D box参数：

4.1 偏航角回归

  仅仅通过目标的图像估计其偏航角是不可能的，因为由下图可以看出，目标的偏航角保持固定的情况下，目标与观察点的相对位置不同也会导致目标的图像不同，这就造成不同图像对应GT相同，即多对一情况，这完全无法训练出准确的结果。

  作者提到，目标的偏航角theta 与 目标中心和相机之间连线的角度theta_ray 以及 目标相对于相机的方向角theta_l之间存在
theta = theta_ray + theta_l 的关系，如下图所示，其中theta_ray直接通过目标偏离图像中心的距离计算得到

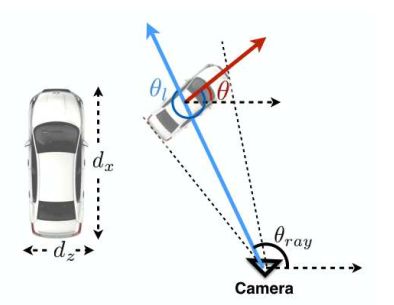
（疑问：感觉角度都是值(标量)的话，这里应该还要减360，即是 theta = theta_ray + theta_l-360°，文中并没有提到这几个角度的方向与正负的关系。。。）

  论文中并没有直接回归theta_l，而是仿照目标检测中锚框这种离散化的设计，将角域（原文这里说的并不是很清楚）划分为n个有重叠的bin，然后预测目标theta_l 在每个bin的置信度以及偏移量△theta

（疑问：为什么要这么做？）

4.2 网络结构

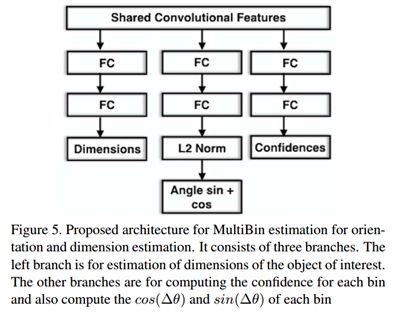
  网络结构并没有什么创新点，简单来说就是在backbone后增加了三个全连接分支，分别用于预测
目标的尺寸、每个bin的角度偏移量（预测的是角度的余弦和正弦）、每个bin的置信度

4.3 损失函数

4.3.1 回归角度部分的损失函数

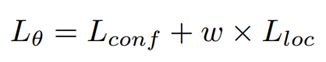
L_conf是每个bin的置信度的softmax loss。

L_loc 是评估 预测角度与Ground Truth的差异的损失函数，如下式所示：

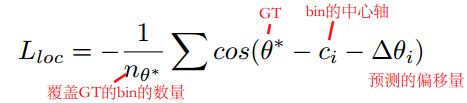
4.3.2 尺寸回归部分的损失函数

这一部分作者使用了L2损失函数，其形式如下



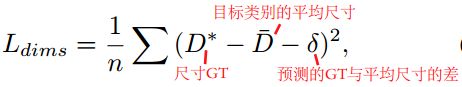
  从这里看到尺寸部分也不是直接预测目标的尺寸，是基于预测的类别信息来对 GT与该类的平均尺寸的差进行回归的（相当于还是偏移量）。
  最后总体的损失函数为上述两者的加权和：

五、 实验

5.1 数据增强

①为GT增加了一定程度的随机扰动（随机小幅度移动）,相应地改变它的标注。目的是增加数据的多样性提升网络泛化能力。
②使用了色彩增强
③使用了镜像的数据增强方式

这里对实验细节等不作分析与记录，感兴趣的读者可以读原论文

5.2 结果展示

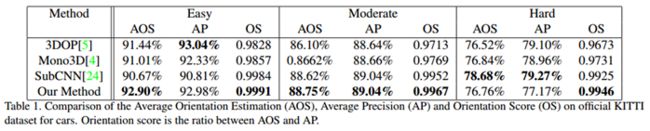
  值得一提的是作者通过特征图与GT得到了热图来分析目标的哪一部分对结果影响较大，可以看出后视镜、车轮等部位对结果影响较大，或者说贡献较大。



最后，文中如有错误的地方请指正，希望大佬能够解答我的那几个疑惑点