【opencv450-samples】digits_svm 手写数字识别SVM vs KNearest (SVM and KNearest digit recognition)
digits.png 样本数据
SVM 和 KNearest 数字识别。
示例从“digits.png”加载手写数字数据集。
然后它训练一个 SVM 和 KNearest 分类器并评估
他们的准确性。
以下预处理应用于数据集:
- 基于矩的图像去偏斜(见去偏斜())
- 数字图像分为 4 个 10x10 单元和 16 个单元
为每个计算定向梯度的直方图
cell
- 使用 Hellinger 度量将直方图转换为空间(参见 [1] (RootSIFT))
[1] R. Arandjelovic, A. Zisserman
"Three things everyone should know to improve object retrieval"
http://www.robots.ox.ac.uk/~vgg/publications/2012/Arandjelovic12/arandjelovic12.pdf
#include "opencv2/core.hpp"
#include "opencv2/highgui.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/imgproc.hpp"
#include "opencv2/ml.hpp"
#include
#include
#include
using namespace cv;
using namespace std;
const int SZ = 20; // size of each digit is SZ x SZ 每个小数字图像的尺寸
const int CLASS_N = 10;//10类
const char* DIGITS_FN = "digits.png";//样本数字图像
static void help(char** argv)
{
cout <<
"\n"
"SVM 和 KNearest 数字识别SVM and KNearest digit recognition.\n"
"\n"
"示例从“digits.png”加载手写数字数据集。Sample loads a dataset of handwritten digits from 'digits.png'.\n"
"Then it trains a SVM and KNearest classifiers on it and evaluates\n"
"their accuracy.然后它训练一个 SVM 和 KNearest 分类器并评估它们的准确性。\n"
"\n"
"以下预处理应用于数据集:Following preprocessing is applied to the dataset:\n"
" - 基于矩的图像偏斜Moment-based image deskew (see deskew())\n"
" - Digit images are split into 4 10x10 cells and 16-bin\n"
" histogram of oriented gradients is computed for each\n"
" cell数字图像是被分成 4 个区域的 10x10 单元格,并为每个单元格计算 16 位定向梯度直方图\n"
" - 使用 Hellinger 度量将直方图转换到空间Transform histograms to space with Hellinger metric (see [1] (RootSIFT))\n"
"\n"
"\n"
"[1] R. Arandjelovic, A. Zisserman\n"
" \"每个人都应该知道改进对象检索的三件事Three things everyone should know to improve object retrieval\"\n"
" http://www.robots.ox.ac.uk/~vgg/publications/2012/Arandjelovic12/arandjelovic12.pdf\n"
"\n"
"Usage:\n"
<< argv[0] << endl;
}
//分割图像image,单元大小cell_size,得到小图像集合cells
static void split2d(const Mat& image, const Size cell_size, vector& cells)
{ //源图像尺寸
int height = image.rows;
int width = image.cols;
//小图像尺寸
int sx = cell_size.width;
int sy = cell_size.height;
cells.clear();//清空集合
for (int i = 0; i < height; i += sy)
{
for (int j = 0; j < width; j += sx)
{
cells.push_back(image(Rect(j, i, sx, sy)));//取小图像区域
}
}
}
//加载样本数字图像fn,分割得到小图像集合digits,以及每个小数字图像对应的标签
static void load_digits(const char* fn, vector& digits, vector& labels)
{
digits.clear();//单个数字图像集合
labels.clear();//单个数字图像标签
String filename = samples::findFile(fn);//数字图像文件
cout << "Loading " << filename << " ..." << endl;
Mat digits_img = imread(filename, IMREAD_GRAYSCALE);//读取数字图像 灰度图
split2d(digits_img, Size(SZ, SZ), digits);//分割数字图像得到单个数字图像
for (int i = 0; i < CLASS_N; i++)//N分类。每行数字对应标签 0 1 2 3 ……
{
for (size_t j = 0; j < digits.size() / CLASS_N; j++)//遍历列
{
labels.push_back(i);//第i行所有列(digits.size() / CLASS_N)对应标签i
}
}
}
//去歪斜 倾斜矫正
static void deskew(const Mat& img, Mat& deskewed_img)
{
Moments m = moments(img);//计算图像三阶矩
if (abs(m.mu02) < 0.01)
{
deskewed_img = img.clone();
return;
}
//mu11/mu02来表示图像的斜切系数,因为图像斜切了,所以原本图像的中心点就移动位置了,所以我们需要将图像的中心点再移动回去,
float skew = (float)(m.mu11 / m.mu02);
float M_vals[2][3] = {{1, skew, -0.5f * SZ * skew}, {0, 1, 0}};//图像的刚体变换矩阵M
Mat M(Size(3, 2), CV_32F);
for (int i = 0; i < M.rows; i++)
{
for (int j = 0; j < M.cols; j++)
{
M.at(i, j) = M_vals[i][j];
}
}
//仿射变换 去歪斜
warpAffine(img, deskewed_img, M, Size(SZ, SZ), WARP_INVERSE_MAP | INTER_LINEAR);
}
//马赛克网格 width:一排多少个小数字
static void mosaic(const int width, const vector& images, Mat& grid)
{
int mat_width = SZ * width;
int mat_height = SZ * (int)ceil((double)images.size() / width);
if (!images.empty())
{
grid = Mat(Size(mat_width, mat_height), images[0].type());//马赛克网格:测试集小图像拼接成grid
for (size_t i = 0; i < images.size(); i++)
{
Mat location_on_grid = grid(Rect(SZ * ((int)i % width), SZ * ((int)i / width), SZ, SZ));//
images[i].copyTo(location_on_grid);
}
}
}
//评估模型 预测结果,测试集样本,测试集标签,可视化评估图像矩阵
static void evaluate_model(const vector& predictions, const vector& digits, const vector& labels, Mat& mos)
{
double err = 0;
for (size_t i = 0; i < predictions.size(); i++)//遍历预测结果集
{
if ((int)predictions[i] != labels[i])
{
err++;//预测失败次数
}
}
err /= predictions.size();//预测错误百分比
cout << format("error: %.2f %%", err * 100) << endl;
int confusion[10][10] = {};//预测结果统计
for (size_t i = 0; i < labels.size(); i++)//遍历测试集
{//测试集第i个样本的标签labels[i],对应行 第i个样本的预测结果标签 对应列。
confusion[labels[i]][(int)predictions[i]]++;// 测试样本i,标签实际为labels[i],预测结果为predictions[i]
}//对角线上的元素为正确预测,非对角线上的元素为错误预测结果
cout << "confusion matrix:" << endl;
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < 10; j++)
{
cout << format("%2d ", confusion[i][j]);//输出预测统计结果
}
cout << endl;
}
cout << endl;
vector vis;//测试集小数字图像向量
for (size_t i = 0; i < digits.size(); i++)//遍历测试集图像
{
Mat img;
cvtColor(digits[i], img, COLOR_GRAY2BGR);//灰度转彩色
if ((int)predictions[i] != labels[i])//测试集样本预测失败
{
for (int j = 0; j < img.rows; j++)
{
for (int k = 0; k < img.cols; k++)
{
img.at(j, k)[0] = 0;
img.at(j, k)[1] = 0;//前两个通道BG置为0. 显示红色小数字图像
}
}
}
vis.push_back(img);
}
mosaic(25, vis, mos);//拼图小数字图像得到mos(红色为错误预测)
}
//1/4 x:梯度图像方向 梯度图像的幅度值weights,16个方向min_length,部分直方图bins
static void bincount(const Mat& x, const Mat& weights, const int min_length, vector& bins)
{
double max_x_val = 0;
minMaxLoc(x, NULL, &max_x_val);//最大梯度方向bin_n
bins = vector(max((int)max_x_val, min_length));//初始化bins
for (int i = 0; i < x.rows; i++)
{
for (int j = 0; j < x.cols; j++)
{
bins[x.at(i, j)] += weights.at(i, j);//方向和幅度相加
}
}
}
//处理小数字图像向量,获得hog描述子矩阵 提取梯度方向直方图hog特征
static void preprocess_hog(const vector& digits, Mat& hog)
{//cell数字图像10x10 被分成 4 个 单元格,并为每个单元格计算 16 位定向梯度直方图
int bin_n = 16;//16 位定向梯度直方图
int half_cell = SZ / 2;//小数字图像尺寸一半
double eps = 1e-7;//迭代条件:精度
hog = Mat(Size(4 * bin_n, (int)digits.size()), CV_32F);//hog描述子矩阵
for (size_t img_index = 0; img_index < digits.size(); img_index++)//遍历所有小数字图像
{
Mat gx;
Sobel(digits[img_index], gx, CV_32F, 1, 0);//梯度gx
Mat gy;
Sobel(digits[img_index], gy, CV_32F, 0, 1);//梯度gy
Mat mag;
Mat ang;
cartToPolar(gx, gy, mag, ang);//笛卡尔转极坐标:幅度、角度 计算每个 2D 向量 (x(I),y(I)) 的幅度、角度或两者:
Mat bin(ang.size(), CV_32S);//
for (int i = 0; i < ang.rows; i++)
{
for (int j = 0; j < ang.cols; j++)
{
bin.at(i, j) = (int)(bin_n * ang.at(i, j) / (2 * CV_PI));//梯度方向 1 …… bin_n
}
}
//梯度方向图分为 4个bin区域。4个bin区域 组合成10x10像素网格
Mat bin_cells[] = {
bin(Rect(0, 0, half_cell, half_cell)),//(0,0,5,5)
bin(Rect(half_cell, 0, half_cell, half_cell)),//(5,0,5,5)
bin(Rect(0, half_cell, half_cell, half_cell)),(0,5,5,5)
bin(Rect(half_cell, half_cell, half_cell, half_cell))(5,5,5,5)
};
Mat mag_cells[] = {
mag(Rect(0, 0, half_cell, half_cell)),
mag(Rect(half_cell, 0, half_cell, half_cell)),
mag(Rect(0, half_cell, half_cell, half_cell)),
mag(Rect(half_cell, half_cell, half_cell, half_cell))
};//梯度幅度分为四个幅度值单元
vector hist;//直方图向量 4*16 个
hist.reserve(4 * bin_n);//reserve的作用是更改vector的容量(capacity),使vector至少可以容纳n个元素。
for (int i = 0; i < 4; i++)//4部分
{
vector partial_hist;//部分直方图:方向bin_n和幅度相加
bincount(bin_cells[i], mag_cells[i], bin_n, partial_hist);
hist.insert(hist.end(), partial_hist.begin(), partial_hist.end());
}
// transform to Hellinger kernel转换为 Hellinger 核
//将得到梯度直方图转化为Hellinger Matrix.
//将梯度直方图Hellinger化,相当于求取了和0向量的海林格距离
double sum = 0;
for (size_t i = 0; i < hist.size(); i++)
{
sum += hist[i];
}
for (size_t i = 0; i < hist.size(); i++)
{
hist[i] /= sum + eps;
hist[i] = sqrt(hist[i]);
}
double hist_norm = norm(hist);
for (size_t i = 0; i < hist.size(); i++)
{
hog.at((int)img_index, (int)i) = (float)(hist[i] / (hist_norm + eps));//hog描述子
}
}
}
//随机数字-洗牌: 打乱顺序的小数字图像及其标签。 标签与图像保持对应关系。
static void shuffle(vector& digits, vector& labels)
{
vector shuffled_indexes(digits.size());//随机数字索引向量
for (size_t i = 0; i < digits.size(); i++)
{
shuffled_indexes[i] = (int)i;//初始化shuffled_indexes: 0 1 2 ……digits.size()-1
}
randShuffle(shuffled_indexes);//随机打乱索引数组
vector shuffled_digits(digits.size());
vector shuffled_labels(labels.size());
for (size_t i = 0; i < shuffled_indexes.size(); i++)
{
shuffled_digits[shuffled_indexes[i]] = digits[i];//根据打乱的索引数组 生成小数字图像向量
shuffled_labels[shuffled_indexes[i]] = labels[i];//根据打乱的索引数组 生成小数字图像的标签向量
}
digits = shuffled_digits;//更新整体数字图像为打乱顺序的数字图像
labels = shuffled_labels;//更新标签向量为 打乱顺序的数字图像对应的标签
}
int main(int /* argc */, char* argv[])
{
help(argv);
vector digits;
vector labels;
load_digits(DIGITS_FN, digits, labels);//加载样本数字图像获得小数字图像集合及分类标签
cout << "preprocessing..." << endl;
// 随机数字 shuffle digits
shuffle(digits, labels);//随机打乱数组元素。 洗牌,保持小数字图像与其标签的对应关系。
vector digits2;//去歪斜的小数字图像向量
for (size_t i = 0; i < digits.size(); i++)//遍历小数字图像
{
Mat deskewed_digit;
deskew(digits[i], deskewed_digit);//小数字图像倾斜校正
digits2.push_back(deskewed_digit);
}
Mat samples;//hog描述子样本矩阵
preprocess_hog(digits2, samples);//计算hog矩阵
//数据集的划分--训练集、验证集和测试集
int train_n = (int)(0.9 * samples.rows);//训练数据集 90%样本
Mat test_set;//测试集
vector digits_test(digits2.begin() + train_n, digits2.end());//测试集图像向量
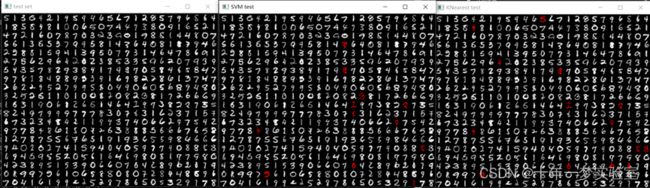
mosaic(25, digits_test, test_set);//测试集图像马赛克:每行25个小数字图像。
imshow("test set", test_set);//显示测试集图像
Mat samples_train = samples(Rect(0, 0, samples.cols, train_n));//训练集样本:hog描述子
Mat samples_test = samples(Rect(0, train_n, samples.cols, samples.rows - train_n));//测试集:hog描述子
vector labels_train(labels.begin(), labels.begin() + train_n);//训练集标签
vector labels_test(labels.begin() + train_n, labels.end());//测试集标签
Ptr k_nearest;//K最近邻(kNN,k-NearestNeighbor)分类算法
Ptr svm;//支持向量机
vector predictions;//samples_test的预测结果
Mat vis;//
cout << "training KNearest..." << endl;
k_nearest = ml::KNearest::create();//静态方法创建空的 K Nearest 分类器。
k_nearest->train(samples_train, ml::ROW_SAMPLE, labels_train);//使用 StatsModel::train 方法对其进行训练。
// 通过K近邻预测数字 predict digits with KNearest
k_nearest->findNearest(samples_test, 4, predictions);//预测
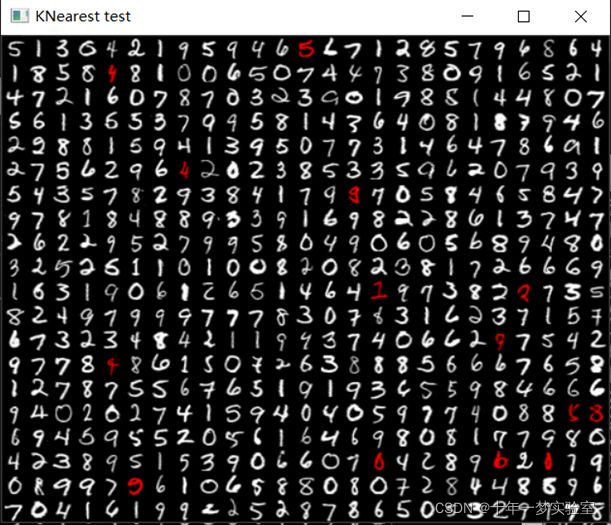
evaluate_model(predictions, digits_test, labels_test, vis);//评估模型预测情况,得到vis拼图(红色表示错误预测)
imshow("KNearest test", vis);//显示K近邻预测结果图(红色表示错误预测)
k_nearest.release();
cout << "training SVM..." << endl;
svm = ml::SVM::create();//使用 StatModel::train 训练模型。 由于 SVM 有多个参数,您可能希望为您的问题找到最佳参数,可以使用 SVM::trainAuto 来完成。
svm->setGamma(5.383);//核函数的参数 gamma。对于 SVM::POLY、SVM::RBF、SVM::SIGMOID 或 SVM::CHI2。 默认值为 1。
svm->setC(2.67);//SVM 优化问题的参数 C。 对于 SVM::C_SVC、SVM::EPS_SVR 或 SVM::NU_SVR。 默认值为 0。
svm->setKernel(ml::SVM::RBF);//使用预定义内核之一进行初始化。
svm->setType(ml::SVM::C_SVC);//SVM 公式的类型。 请参阅 SVM::类型。 默认值为 SVM::C_SVC。
svm->train(samples_train, ml::ROW_SAMPLE, labels_train);//训练
//使用SVM预测数字 predict digits with SVM
svm->predict(samples_test, predictions);//预测测试集样本
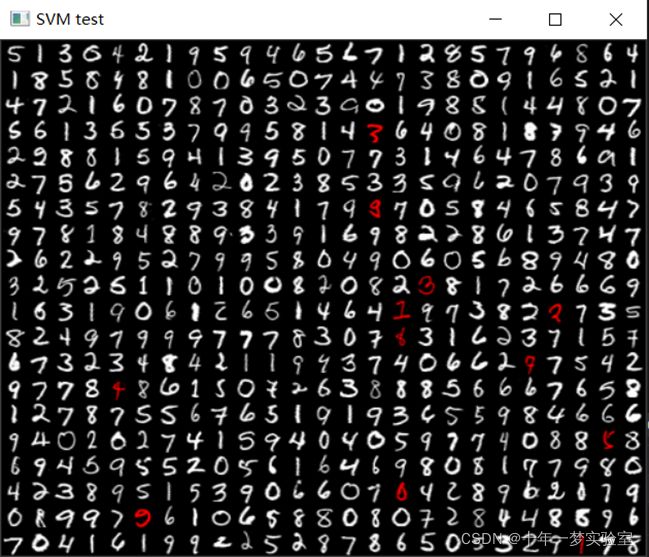
evaluate_model(predictions, digits_test, labels_test, vis);//评估预测结果
imshow("SVM test", vis);//显示预测结果(红色表示失败)
cout << "Saving SVM as \"digits_svm.yml\"..." << endl;
svm->save("digits_svm.yml");//保存SVM参数
svm.release();
waitKey();
return 0;
}
运行结果
preprocessing...
training KNearest...
error: 2.80 %
confusion matrix:
42 1 0 0 0 0 1 0 0 0
0 45 1 0 0 0 0 0 0 0
0 0 45 0 0 0 0 0 0 1
0 0 0 34 0 0 0 0 0 0
0 0 0 0 43 0 0 0 2 1
0 0 0 0 0 49 1 0 1 0
1 0 0 0 0 0 55 0 0 0
0 0 0 0 0 0 0 55 1 0
0 0 0 1 0 0 0 0 62 0
0 0 0 1 0 0 0 0 1 56
training SVM...
error: 2.40 %
confusion matrix:
43 0 0 0 0 0 1 0 0 0
0 44 1 0 0 0 0 1 0 0
0 0 45 0 0 0 0 0 0 1
0 0 0 32 0 0 0 1 0 1
0 0 0 0 45 0 0 0 1 0
0 0 0 0 0 50 1 0 0 0
0 0 0 0 0 0 56 0 0 0
0 0 0 0 0 0 0 55 1 0
0 0 0 0 1 0 0 0 62 0
0 0 1 0 1 0 0 0 0 56
Saving SVM as "digits_svm.yml"...
笔记:
/** @brief 随机打乱数组元素。Shuffles the array elements randomly.
函数 cv::randShuffle 通过随机选择元素对并交换它们来打乱指定的一维数组。 此类交换操作的数量将为 dst.rows\*dst.cols\*iterFactor .
@param dst 输入/输出数字一维数组input/output numerical 1D array.
@param iterFactor scale factor that determines the number of random swap operations (see the details below). 决定随机交换操作数量的比例因子(请参阅下面的详细信息)。
@param rng optional random number generator used for shuffling; if it is zero, theRNG () is used instead. 用于洗牌的可选随机数生成器; 如果为零,则使用 theRNG() 代替。
@sa RNG, sort
*/
CV_EXPORTS_W void randShuffle(InputOutputArray dst, double iterFactor = 1., RNG* rng = 0);
/** @brief 查找近邻并预测输入向量的响应。
@param samples 按行存储的输入样本。它是一个 ` * k` 大小的单精度浮点矩阵。
@param k 使用的最近邻居数。应该大于 1。
@param results 带有每个输入样本的预测结果(回归或分类)的向量。它是一个带有 `` 元素的单精度浮点向量。
@param neighborResponses 对应邻居的可选输出值。它是一个 ` * k` 大小的单精度浮点矩阵。
@param dist 从输入向量到相应邻居的可选输出距离。它是一个 ` * k` 大小的单精度浮点矩阵。
对于每个输入向量(矩阵样本的一行),该方法会找到 k 个最近邻。
在回归的情况下,预测结果是特定向量的邻居响应的平均值。在分类的情况下,通过投票确定类别。
对于每个输入向量,邻居按它们到向量的距离排序。
在 C++ 接口的情况下,您可以使用指向空矩阵的输出指针,函数将自行分配内存。
如果只传递一个输入向量,则所有输出矩阵都是可选的,并且预测值由方法返回。
该函数与 TBB 库并行化。
*/
CV_WRAP virtual float findNearest( InputArray samples, int k,
OutputArray results,
OutputArray neighborResponses=noArray(),
OutputArray dist=noArray() ) const = 0;
/** @brief 计算多边形或光栅化形状的所有三阶矩。Calculates all of the moments up to the third order of a polygon or rasterized shape.
The function computes moments, up to the 3rd order, of a vector shape or a rasterized shape. The results are returned in the structure cv::Moments. 该函数计算向量形状或光栅化形状的最高 3 阶矩。 结果在结构 cv::Moments 中返回。
@param array Raster image (single-channel, 8-bit or floating-point 2D array) or an array (\f$1 \times N\f$ or \f$N \times 1\f$ ) of 2D points (Point or Point2f ). 光栅图像(单通道、8 位或浮点二维数组)或二维点(Point 或 Point2f)的数组(乘 N 或 N 乘 1)。
@param binaryImage If it is true, all non-zero image pixels are treated as 1's. The parameter is used for images only. 如果为真,则所有非零图像像素都被视为 1。 该参数仅用于图像。
@returns moments矩.
@note Only applicable to contour moments calculations from Python bindings: Note that the numpy type for the input array should be either np.int32 or np.float32. 仅适用于 Python 绑定的轮廓矩计算:请注意,输入数组的 numpy 类型应为 np.int32 或 np.float32。
@sa 轮廓区域,弧长contourArea, arcLength
*/
CV_EXPORTS_W Moments moments( InputArray array, bool binaryImage = false );KNN定义
✔️ K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一, 通俗理解它,就是近朱者赤,近墨者黑。
KNN原理
✔️ 为了判断未知样本的类别,以所有已知类别的样本作为参照,计算未知样本与所有已知样本的距离,从中选取与未知样本距离最近的K个已知样本,根据少数服从多数的投票法则(majority-voting),将未知样本与K个最邻近样本中所属类别占比较多的归为一类
算法的描述
1)计算测试数据与各个训练数据之间的距离;
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。
优点
1.简单,易于理解,易于实现,无需估计参数,无需训练;
2.适合对稀有事件进行分类;
3.特别适合于多分类问题, kNN比SVM的表现要好。
缺点
1> 当训练数据集很大时,需要大量的存储空间,而且需要计算待测样本和训练数据集中所有样本的距离,所以非常耗时;
2> KNN对于样本不均衡,以及随机分布的数据效果不好。
算法的使用场景:
1、适合用于类别间差异较大,同类别间数据差异较小的场景;
2、对于类别间的界限不清晰的场景,效果好于基于线性分类的逻辑回归;
3、单个测试样本计算都需要计算与训练集中所有训练样本的距离,在数据量较大时会占用非常多的计算力并增加计算时间;
4、对于各个类别中数据数量差异较大的场景效果较差,特别在K取值又较大时,占数量优势的类别对于结果的影响非常明显。
参考:
机器学习算法—KNN算法原理及阿里云PAI平台算法模块参数说明-阿里云开发者社区 (aliyun.com)![]() https://developer.aliyun.com/article/722515?spm=a2c6h.13148508.0.0.45304f0eaHYhmN
https://developer.aliyun.com/article/722515?spm=a2c6h.13148508.0.0.45304f0eaHYhmN
OpenCV图像处理-KNN&决策树算法 - 知乎 (zhihu.com)![]() https://zhuanlan.zhihu.com/p/85636009
https://zhuanlan.zhihu.com/p/85636009
opencv手写数字识别:SVM和KNearest - 知乎 (zhihu.com)![]() https://zhuanlan.zhihu.com/p/401039799
https://zhuanlan.zhihu.com/p/401039799
基于视觉的特征匹配算法(持续更新) - 知乎 (zhihu.com)![]() https://zhuanlan.zhihu.com/p/147325381
https://zhuanlan.zhihu.com/p/147325381
(四十五)OpenCV中的机器学习-用SVM做图像识别 - 知乎 (zhihu.com)![]() https://zhuanlan.zhihu.com/p/93224022
https://zhuanlan.zhihu.com/p/93224022