机器学习笔记-感知机对偶形式

---

前言

  感知机模型是有两种形式的，上一篇文章中详细学习了感知机的原始形式数学模型，我们知道，感知机应该还有对偶形式，这篇文章就来记录一下感知机对偶形式的的数学模型。

一、感知机对偶形式

  我们知道感知机的学习算法可以解释为：当一个实例点被误分类时，即位于分离超平面的错误一侧时，则根据这个误分类点来调整$w$和$b$的值，使分离超平面向误分类点的一侧移动，以减少该误分类点与超平面之间的距离，直到超平面能够越过该误分类点使其被正确分类。
  从上面可以理解，超平面的学习是只与误分类点有关，在原始的感知机模型中，我们说使用梯度下降法来学习感知机，这种学习方式其实是逐步逐步进行学习，且推导过$w$和$b$这两个参数的迭代过程如下：
$$w\leftarrow w+\eta y_i{x}_i$$
$$b\leftarrow b+\eta y_i$$
  上述的迭代过程是如果有一次误分类点，就迭代一次，那我们可以假设样本点$(x_i,y_i)$的误分类次数为$n_i$，设样本点的个数为$N$，就可以推导出$w$和$b$的表达式如下：
$$w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$$
$$b=\sum _{i=1}^N{\alpha }_i{y}_i$$
  其中${\alpha }_i=n_i\eta$，这样我们就可以认为，只要找到所有样本点的更新次数，我们就能求出$w$和$b$。同时感知机的数学模型也就可以转换成如下形式：
$$sign(x)=sign(wx+b)=sign(\sum _{j=1}^N{n}_j\eta y_j{x}_j\cdot x+\sum _{j=1}^N{n}_j\eta y_j)$$
  此时学习的目标就不是$w$和$b$了，而是$n_i,i=1,2,3,\cdots ,N$。于是可以得到感知机对偶形式的学习算法如下：

1. 初始化学习率$\eta =0.1$，令$n_i$等于0，其中$i=1,2,3,\cdots ,N$；
2. 在训练集中选取数据$(x_i,y_i)$;
3. 如果$y_i(\sum _{j=1}^N{n}_j\eta y_j{x}_j\cdot x_i+\sum _{j=1}^N{n}_j\eta y_j)\le 0$，则$n_i=n_i+1$；
4. 转至2，直到没有误分类点出现；

这里需要解释一下，判断是否是误分类点的依据前面已经说过了，就是：
$$y_i(w{x}_i+b)\le 0$$
这里只不过是把$(w{x}_i+b)$换成$(\sum _{j=1}^N{n}_j\eta y_j{x}_j\cdot x_i+\sum _{j=1}^N{n}_j\eta y_j)$

二、感知机对偶形式的实现

  感知机的对偶形式，相比原始形式，其实最大的变化就是需要提前计算样本点的内积，也就说可以用一个矩阵提前存储样本点的内积：
$$G={\left[x_i\cdot x_j\right]}_{N\times N}$$
  提前计算样本的内积可以为后续计算节省时间，这样可以大大提高效率。
代码如下：

%% 感知机
clc,clear
tic
% 随机初始化数据
random = unifrnd(1,5,40,2);
X = [random(1:20,:);random(21:40,:)+5];
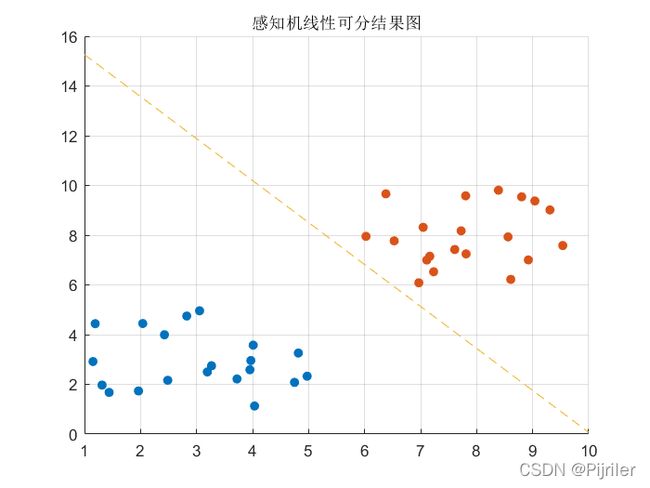
scatter(X(1:20,1),X(1:20,2),'o','filled')
hold on
scatter(X(21:40,1),X(21:40,2),'o','filled')
y = [zeros(20,1)-1;ones(20,1)]; % y标签
learn_rate = 0.1; % 定义学习率
% 感知机进行线性分类_对偶形式
ni = zeros(length(X),1); % 记录每个样本误分类的次数
% 计算Gram矩阵
G = zeros(length(X),length(X));
for i = 1:length(X)
    for j = 1:length(X)
        G(i,j) = X(i,:) * X(j,:)';
    end
end
while flag ~= length(X)
    flag = 0;
    for i =1:length(X) % 遍历所有样本点
        if y(i)*(G(i,:)*(ni*learn_rate.*y)+learn_rate*ni'*y)<=0
            ni(i) = ni(i)+1;
            break; % 跳出循环
        else
            flag = flag + 1;
        end
    end
end

% 结果可视化
w = (learn_rate * ni .* y)' * X;
b = learn_rate * ni'* y;
k = - w(1) / w(2); % 求斜率
b = - b / w(2); % 求系数
n = 1:1:10;
m = k * n + b;
hold on
plot(n,m,'--')
grid on
title('感知机线性可分结果图')
toc

结果如图：

总结

  其实感知机的原始形式和对偶形式并没有本质的区别，对偶形式的意义就是可以提前计算样本点特征向量之间的内积，也就是Gram矩阵，这样在后续学习的过程中就可以加快计算速度。