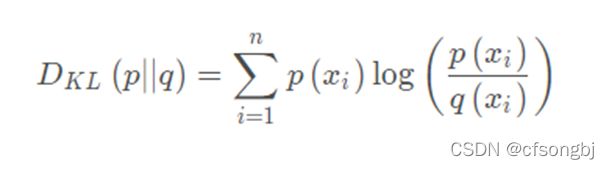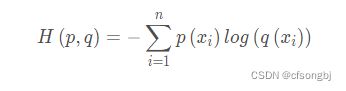【PraNet】论文代码解读（损失函数部分）——Blank

文中采用的总体损失为：

其中IoU为交并比，BCE为二元交叉熵。在计算损失时使用加权值得方式，使整个模型偏向图像中物体的边缘部分。

关于加权，文中取像素值周围15个像素值（上下左右个各15个），形成31*31的矩阵。计算矩阵中数值的平均值，之后计算平均值与该像素值的差值，这样可以计算该像素点与周围像素点的差异。由于我们只在乎差异的大小，所以需要取绝对值。

weit = 1 + 5*torch.abs(F.avg_pool2d(mask, kernel_size=31, stride=1, padding=15) - mask)

以上计算可以理解为，我们关注图像中每个像素点与周围的区别，那么可以想象，一个只有黑与白的图像，什么地方的像素点与周围的图像差别最大呢（没错，就是黑白交接的地方）。所以通过在损失计算时通过添加权值，可以使模型更加关注图像的边缘部分。

---

关于IoU的计算

以下内容参考机器学习——概念理解之IoU_helpburn的博客-CSDN博客_机器学习iou

IoU(Intersection over Union)：交并比，在SSD的论文中也叫Jaccard Overlap，是一个意思。从字面意思上看是交集和并集的比值。

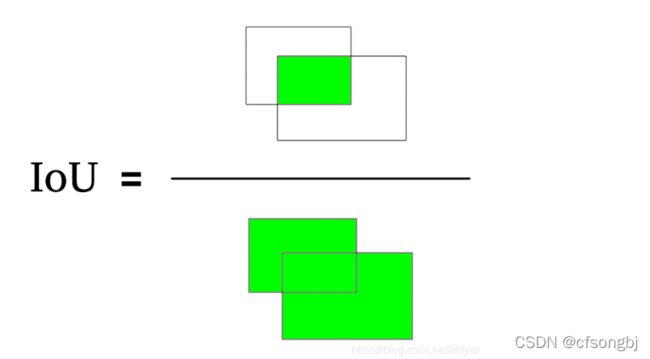
IoU最初是使用在计算机视觉中的图像捕捉中，检验准确率。计算方法如下图所示

 

后来运用到机器学习中，成为计算损失函数的一种很好的工具，不过为了使函数可导，通常IoU的计算方式为下：

 代码为：

pred = torch.sigmoid(pred)
inter = ((pred * mask)*weit).sum(dim=(2, 3))
union = ((pred + mask)*weit).sum(dim=(2, 3))
wiou = 1 - (inter + 1)/(union - inter+1)

---

关于BCE二元交叉熵，

以下内容参考交叉熵损失函数原理详解_Cigar丶的博客-CSDN博客_交叉熵损失函数

信息奠基人香农认为“信息是用来消除随机不确定性的东西，也就是衡量信息量的大小，就是看这个消息消除不确定性的程度。

 信息熵用来表示所有信息量的期望,期望是实验中每次可能结果的概率乘以其结果的总和。

 相对熵用来计算对于同一个随机变量X有两个单独的概率分布P(X)与Q(X)之间的差异。

在机器学习中我们计算预测集与标签集之间的差异，由于标签集是确定的，我们可将相对熵拆开：

 

 所以交叉熵的公式为

在二分类情况下 使用二元交叉熵公式为：

 

文中代码为：

wbce = F.binary_cross_entropy_with_logits(pred, mask, reduce='none')
wbce = (weit*wbce).sum(dim=(2, 3)) / weit.sum(dim=(2, 3))

 

---

全部的损失计算为：

def structure_loss(pred, mask):
    weit = 1 + 5*torch.abs(F.avg_pool2d(mask, kernel_size=31, stride=1, padding=15) - mask)

    wbce = F.binary_cross_entropy_with_logits(pred, mask, reduce='none')
    wbce = (weit*wbce).sum(dim=(2, 3)) / weit.sum(dim=(2, 3))

    pred = torch.sigmoid(pred)
    inter = ((pred * mask)*weit).sum(dim=(2, 3))
    union = ((pred + mask)*weit).sum(dim=(2, 3))
    wiou = 1 - (inter + 1)/(union - inter+1)
    return (wbce + wiou).mean()

 

---

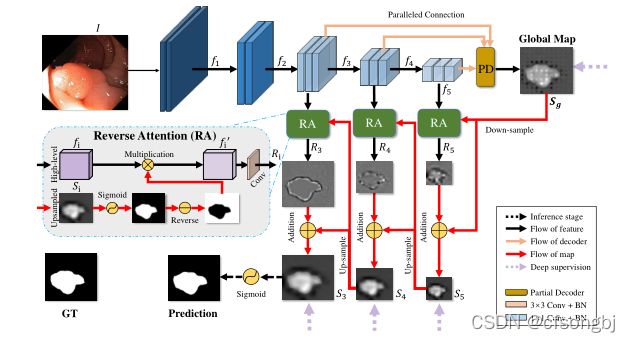
 项目中虚线箭头Deep supervison 表示计算损失。