Conv2Former: A Simple Transformer-Style ConvNet for Visual Recognition

论文: https://arxiv.org/pdf/2211.11943.pdf
code(pytorh版本): https://github.com/shanglianlm0525/PyTorch-Networks

一、引言

本文并没有试图设计一种最先进的视觉识别方法，而是研究了一种更有效的方法，利用卷积来编码空间特征。通过比较最近的卷积神经网络(ConvNets)和Vision transformer的设计原理，提出利用卷积调制操作来简化自注意。本文证明了这样一个简单的方法可以更好地利用嵌套在卷积层中的大内核(≥7 × 7)。使用所提出的卷积调制(称为Conv2Former)构建了一个层次ConvNets家族。
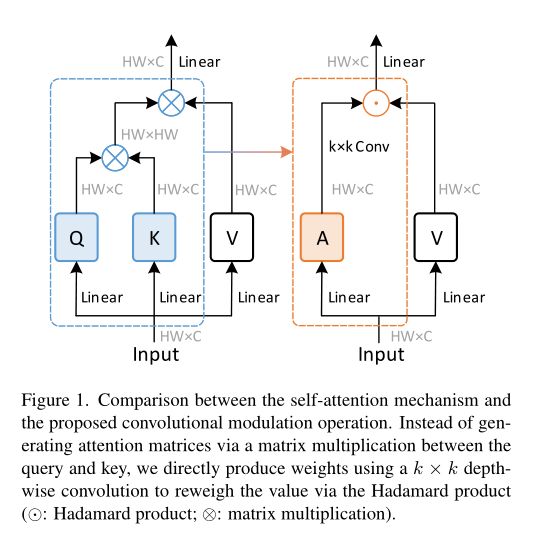
本文比较了vit和ConvNets用于编码空间信息的不同方式。如下图左侧所示，自注意通过其他所有位置的加权和来计算每个像素的输出。这个过程也可以通过计算大核卷积输出和值表示之间的Hadamard乘积来模拟，我们称之为卷积调制，如下图的右侧所示。
不同之处在于卷积核是静态的，而自注意生成的注意矩阵可以适应输入。实验表明，使用卷积来生成权值矩阵也有很好的效果。

简单地将ViTs中的自注意替换为所提出的卷积调制操作，就得到了所提出的网络，称为Conv2Former。它背后的含义是使用卷积来构造一个Transformer-style的ConvNet，其中卷积特征被用作权重来调制值表示。与经典的具有自注意力的vit相比，本文的方法，像许多经典的ConvNets一样，是完全卷积的，因此它的计算量线性增加，而不是像Transformer那样，随着图像分辨率的提高而呈二次增长。这使得本方法对下游任务更友好，比如对象检测和高分辨率语义分割。Conv2Former可以从更大的内核(如11×11和21×21)的卷积中获益更多。这与之前的ConvNets得出的结论不同，后者表明使用内核大小大于9×9的标准深度卷积几乎不会带来性能提升，但会增加计算负担。本文的方法比最近使用超大核卷积的工作表现得更好。

二、架构实现

整体架构如下图所示。与ConvNeXt和Swin Transformer网络类似，Conv2Former也采用了金字塔架构。总共有四个阶段，每个阶段都有不同的特征映射分辨率。

在连续两个阶段之间，采用贴片嵌入块来降低分辨率，通常是2 × 2的卷积，步幅为2。不同的阶段有不同数量的卷积块。本文构建了五个Conv2Former变体，即Conv2Former- n, Conv2Former- t, Conv2Former- s, Conv2Former- b, Conv2Former- l。详见下表。

当可学习参数数量固定时，如何安排网络的宽度和深度会影响模型的性能。原来的ResNet-50将每个阶段的块数设置为(3,4,6,3)，而ConvNeXt-T则遵循Swin-T的原则将块数更改(3,3,9,3)，并对较大的模型使用1:1:1:9:1的阶段计算比例。本文稍微调整了比例，如上表所示。我们观察到，对于一个微小的模型(参数小于30M)，更深的网络表现更好。
四种不同的微型模型之间的简单比较可以在下表中找到。

(一)、Convolutional Modulation Block

在每个阶段使用的卷积块具有与Transformer相似的结构，主要包含用于空间编码的自注意层和用于通道混合的FFN。不同的是，本文用简单的卷积调制层取代了自注意层。
在卷积调制层中，不是通过点积计算相似度评分矩阵A。而是通过卷积特征对V值进行调制，简化了自注意。具体来说，给定输入令牌$X\in R^{H\times W\times C}$，我们使用核大小为k × k的简单深度卷积和Hadamard乘积来计算输出Z，如下所示:

.为Hadamard积，$W_1$和$W_2$为两个线性层的权值矩阵，DConvk×k为核大小为k×k的深度卷积，通过上述卷积调制运算，可以使每个空间位置(h, w)与以(h, w)为中心的k×k平方区域内的所有像素相关联，通道之间的信息交互可以通过线性层实现。每个空间位置的输出是正方形区域内所有像素的加权和。
残差块、自注意和所提出的调制块之间的对比图如下所示。与自注意力相比，本方法利用卷积来建立关系，这比自注意更节省内存，尤其是在处理高分辨率图像时。与经典残差块[相比，由于调制操作，我们的方法也能适应输入内容。

（二）、微观设计

内核比7×7大。如何利用空间卷积是卷积网络设计的重要内容。自VGGNet和ResNets以来，3 × 3卷积一直是构建ConvNets的标准选择。后来，深度可分离卷积的出现改变了这种情况。ConvNeXt表明，将ConvNets的核大小从3扩大到7可以提高分类性能。然而，进一步增加内核大小几乎不会带来性能上的提升，反而会在没有重新参数化的情况下增加计算量。我们认为，让ConvNeXt从大于7 × 7的内核大小中获益很少的原因是使用空间卷积的方式。对于Conv2Former，当内核大小从5 × 5增加到21 × 21时，我们观察到一致的性能增益。这种现象不仅出现在Conv2Former-T(82.8→83.4)中，也出现在参数为80M+的Conv2Former-B(84.1→84.5)中。
权重的策略。如上图(d)所示，将深度卷积的输出作为权重，对线性投影后的特征进行调制。值得注意的是，在Hadamard积之前，既没有使用激活层，也没有使用归一化层(例如Sigmoid或Lp归一化层)。这是获得良好表现的必要因素。例如，在SENet中添加Sigmoid函数会使性能降低0.5%以上。
FocalNet采用了与本文相似的加权策略，但其动机不同。
FocalNet旨在通过3×3深度卷积和全局平均池化来提取多层次的特征，以进行分层上下文聚合。而本文试图通过利用简单的大核卷积来简化自注意力操作，并研究一种有效的方法来使用ConvNets的大核空间卷积。本方法比FocalNet简单得多，实验证明了Conv2Former比FocalNet的优势。
归一化和激活。对于归一化层，沿用了原有的ViT和ConvNeXt，采用层归一化代替了广泛使用的批归一化。对于激活层，使用GELU。层归一化和GELU的组合带来了0.1%-0.2%的性能增益。

三、实验

（一）、分类

(二)使用大核卷积

使用大核卷积是一种帮助CNN建立远程关系的直接方法。然而，在现有的基于CNN的架构中直接使用大核卷积(> 7 × 7)使得识别模型难以优化。最近，有一些工作旨在开发新技术来唤起大核卷积在cnn中的应用。在下表中，展示了最近最先进的具有不同内核大小的ConvNets的结果。可以看到，在没有任何其他训练技术的情况下，比如重参数化或使用稀疏权重，核大小为7 × 7的Conv2Former在基本模型设置下已经比其他方法表现得更好。使用更大的内核大小11 × 11可以获得更好的性能增益。这些结果反映了卷积调制块的优势。

(三)、消融实验

（1）、内核大小。

ConvNeXt的工作表明，当深度卷积的核大小大于7 × 7时，没有性能增益。在这里，研究了当内核变大时模型性能的变化。为深度卷积选择了6个不同的核，即{5 × 5,7 × 7,9 × 9,11 × 11,15 × 15,21 × 21}，并基于Conv2Former-T和Conv2Former-B两种模型变体展示了结果。结果如下(a)所示。在内核大小增加到21 × 21之前，性能增益似乎已经饱和。这个结果与ConvNeXt得出的结论截然不同，ConvNeXt得出的结论是，使用大于7 × 7的内核不会带来明显的性能提升。这表明使用卷积特征作为权重的公式可以比传统方法更有效地利用大的内核。

(2)、Hadamard积优于求和。

利用深度卷积提取的卷积特征，通过Hadamard积运算来调制右线性分支的权值。
实验中，还尝试利用元素的总和来融合两个分支。上图显示了Conv2Former在不同模型尺寸下的对比结果。Hadamard积的性能优于按元素求和，表明卷积调制在编码空间信息方面比求和更有效。小型模型从Hadamard产品中受益更多。

（3）、权重的策略。

除了上述两种融合策略外，还尝试使用其他方法来融合特征图，包括添加Sigmoid函数，应用L1归一化，将值线性归一化到(0,1)。结果汇总见表下表。可以看到Hadamard比其他所有操作的结果更好。当使用Sigmoid函数或线性归一化(0,1)将A的值调整为正值时，性能下降得更多。这与传统的注意力机制不同，比如SE和CA在重新权衡之前利用Sigmoid函数。

(4)、Results on Isotropic Models to ViTs

与采用层次结构的经典CNN不同，由于自注意层较重，vanilla ViT采用了包含补丁嵌入层和相同序列长度的transformer堆栈的普通架构。这种朴素的架构在最近的Transformer中被广泛使用。在这里，遵循ConvNeXt，并试图研究Conv2Former在ViT style架构设置下的性能。与ConvNeXt类似，将Conv2Former-IS和Conv2Former-IB的块数设置为18，并调整通道数以匹配模型大小。
下表显示了结果。以DeiT-S和DeiT-B模型为基准。为简洁起见，在模型名称中添加了一个字母“I”，表示相应的模型使用各向同性体系结构作为原始ViT。对于22M参数左右的小型模型，我们的Conv2Former-IS比DeiT-S和表现要好得多,性能增益约为1.5%。当将模型尺寸放大到80M+时，Conv2Former-IB达到了82.7%的top-1精度分数，这也比ConvNeXt-IB好0.7%，比DeiTB好0.9%。此外，使用三次卷积进行补丁嵌入可以进一步改善结果。

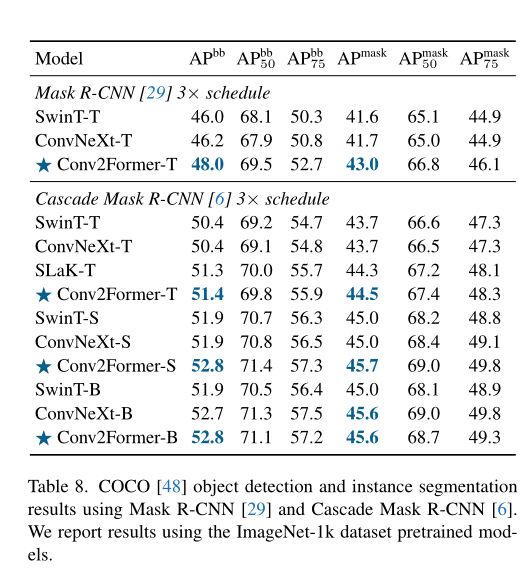
(四)、目标检测

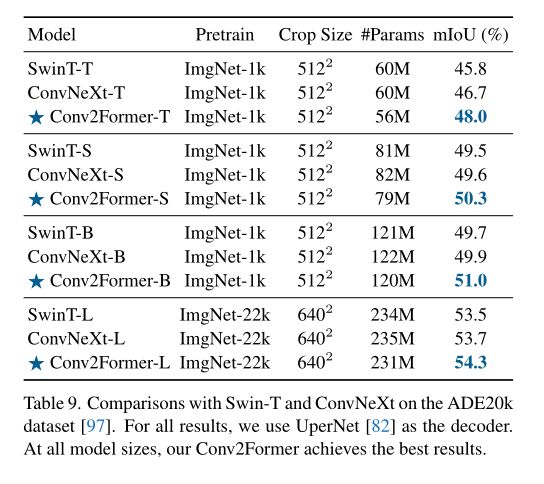
（五）、语义分割

四、代码实现

class ConvMod(nn.Module):
    def __init__(self, dim):
        super().__init__()
        self.norm = LayerNorm(dim, eps=1e-6)
        self.a = nn.Sequential(
            nn.Conv2d(dim, dim, 1),
            nn.GELU(),
            nn.Conv2d(dim, dim, 11, padding=5, groups=dim)
        )
        self.v = nn.Conv2d(dim, dim, 1)
        self.proj = nn.Conv2d(dim, dim, 1)
    
    def forward(self, x):
        B, C, H, W = x.shape
        x = self.norm(x)
        a = self.a(x)
        v = self.v(x)
        x = a * v
        x = self.proj(x)
        return x