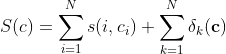近邻传播 Affinity Propagation(AP) 聚类算法原理及实现

1.概述

      机器学习中 AP(Affinity Propagation)通常被称为近邻传播算法或者密切度传播或类同传播算法，由 Frey 与Dueck于2007年在Science首次提出。AP算法的基本思想是将全部数据点都当作潜在的聚类中心(称之为exemplar)，然后数据点两两之间连线构成一个网络(相似度矩阵)，再通过网络中各条边的消息(responsibility和availability)传递计算出各样本的聚类中心（cluster center）。

2.算法原理

2.1 算法思想

     不同于K均值聚类等算法需要提前设置簇数量K，这种方法自动确定簇的数量。对于聚类对象中每个数据点都选择另一个数据点作为其范例(exemplar)或质心（centroid）。更准确地说，让表示数据点   的簇中心,表示数据点的总数量。优化对象是最大化如下函数

                                        

其中，右边第一项衡量每个数据点  与它对应的簇中心  之间的相似度。第二项是惩罚项，如果某个数据点  选择 数据点  作为它的簇中心 ，但是数据点 并不选择它自己作为所在簇中心，那么此时相应地惩罚项就是。

                                

对于上述相似性的衡量，通常选择两两数据点之间的负欧式距离来表示。

                                                

对于负欧式距离的提法，可以理解为当得到一个依赖于簇中心的概率模型时，会被设置成点的簇中心是点   的 log-likelihood。

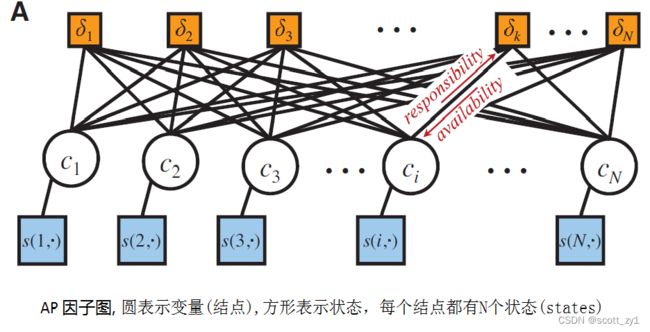
将数据点视为网络中的结点，上述目标函数可表示为因子图如下。

上述优化对象(函数)通常采用max-product loopy belief propagation进行求解，迭代示意图如下。

2.2 算法流程

在完整的算法流程前，首先引入4个概念：similarity、preference、responsibility、availability。

1）similarity

       similarity即相似度， 按照上述方法计算负欧氏距离作为反映数据点  与数据点  的相似度值，相似度值越大表示数据点  与  的距离越近，AP算法中理解为数据点  作为数据点  的聚类中心的能力，作为算法的初始化矩阵，个点就有由个相似度值组成的相似度（Similarity）矩阵；

2）preference
       preference称之为参考度或偏好度，是相似度矩阵中对角元素，如，若按负欧氏距离计算其值应为0，但在AP聚类中其反映数据点  作为聚类中心的程度，因此不能为0。迭代开始前假设所有点成为聚类中心的能力相同，因此参考度初始化一般设为相似度矩阵中所有值的中位数或最小值，设为中位数意味着迭代得到的簇数量倾向于中位簇数量，最小值则倾向于得到最小簇数量。参考度越大则说明这个数据点成为聚类中心的能力越强。

3）responsibility 与 availability
       responsibility 是点 传递信息到候选的簇中心点  的取值，描述数据点  适合作为数据点 的聚类中心的程度，考虑了点  的别的潜在簇中心(见Fig.B)，availability 是从候选簇中心点 传递信息到点  的取值  , 反映了点  选择  作为它的簇中心的合适程度，考虑了除点外别的点对点  作为簇中心的支持（见 Fig.C）。

        

 具体的迭代过程如下：

a) 初始化时，上述 ， 然后按下述规则计算出 responsibilities，

        
                                         

b) 第一次迭代时，因为Availabilities都是0，那么,  被设置成输入的点  与候选的点 (exemplar )之间的相似度减去点  和其他候选聚类中心 之间的最大相似度。这个竞争更新过程是数据驱动的，并不考虑有多少其它的点支持每个候选聚类中心。

c) 在后面的迭代中，当一些点被有效地分配给其它聚类中心，它们的availabilities将会降到零值以下。详细更新规则见下文。这些负的availabilities会减小上面规则中的输入相似度  的有效值，因 ，从而使相应的候选聚类中心  被排除在外。

d) 当 时，相应地  被设置成  作为聚类中心的的偏好度preference的取值  减去点  和其它所有候选聚类中心的最大相似度。此时"self-responsibility"即  基于输入合适的preference（右边第一项）以及  多么不适合分配给另一个聚类中心（右边第二项），来综合反映   适合 成为一个聚类中心。

e) 鉴于上面的responsibility 的更新让所有的候选簇中心竞争数据点的控制权，下面的 availibility更新从数据点积累关于是否每个候选聚类中心都会是一个好的聚类中心的判据，具体更新过程如下：

                        

availibility的取值  被设置成self-responsibility 的取值  加上候选的聚类中心 从其它点获得的正responsibilities的总和。只有正responsibilities是会被添加进来的，因为对于一个好的聚类中心只负责解释部分有responsibilities的数据点，而不用管有负的responsibilities的数据点。如果self-responsibility 取值是负的（表明点 目前更适合作为另一个簇中心点的支持点而不是成为一个簇中心点）。如果一些其它点支持点 作为它们的簇中心， 作为一个簇中心点的availibility能够增加，也就是相应地会取正值。上式中为了限制得到的正responsibilities的影响力，这个总和是被限定的，即它不能大于0。而 self-availability的取值  的更新是不一样的，具体如下：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

上式表明其它点传递给候选聚类中心正responsibilities 来反映点 成为一个聚类中心的积累过程。

上述更新计算要求简单，所传递的信息只在具有已知相似度之间的数据点对之间交换。在AP算法的实现过程中，任何点的availabilities和responsibilities都与定义聚类中心相关联。

f) 为防止数据震荡，引入阻尼系数(damping factor)，responsibilities 迭代更新时，每个responsibilities取值等于前一次迭代更新的信息值的 倍加上此轮更新值的  倍，其中在取值0-1之间，通常取0.5，即前后两次加权平均。

2.3 算法特点

优点：

1. 不需要制定最终聚类簇的个数
2. 已有的数据点形成最终的聚类中心，而不是新生成一个簇中心
3. 模型对数据的初始值不敏感
4. 对初始相似度矩阵数据的对称性没有要求
5. 与k-means及其变种等聚类方法相比，其结果的平方误差较小。

不足：

1. 不用提前设置簇中心数量，需事先设置参考度，而参考度的大小与聚类中心的个数正相关；
2. 每次迭代都需要更新每个数据点的responsibility 和availibility，算法复杂度较高，在大数据量下运行时间较长。

3.代码实现

sklearn.cluster.AffinityPropagation(damping=0.5, max_iter=200, convergence_iter=15, copy=True, preference=None, affinity='euclidean', verbose=False)

参数设置介绍：

• damping : 阻尼系数或称衰减系数，默认为0.5
• convergence_iter : 迭代次后聚类中心没有变化，算法结束，默认为
• max_iter : 最大迭代次数，默认
• copy : 是否在元数据上进行计算，默认True，在复制后的数据上进行计算。
• preference : S的对角线上的值
• affinity :S矩阵（相似度），默认为euclidean（欧氏距离）矩阵，即对传入的X计算距离矩阵，也可以设置为precomputed，那么X就作为相似度矩阵。

训练完AP聚类之后可以获得的结果有

• cluster_centers_indices_ : 聚类中心的位置
• cluster_centers_ : 聚类中心
• labels_ : 类标签
• affinity_matrix_ : 最后输出的A矩阵
• n_iter_ ：迭代次数

4.参考文献

Frey B J, Dueck D. Clustering by passing messages between data points[J]. science, 2007.